Презентація на тему:
Аксіоми стереометрії

Аксіоми стереометрії. Деякі наслідки з аксіом.

Геометрія Планіметрія Стереометрія stereos тіло, твердий, обємний , просторовий

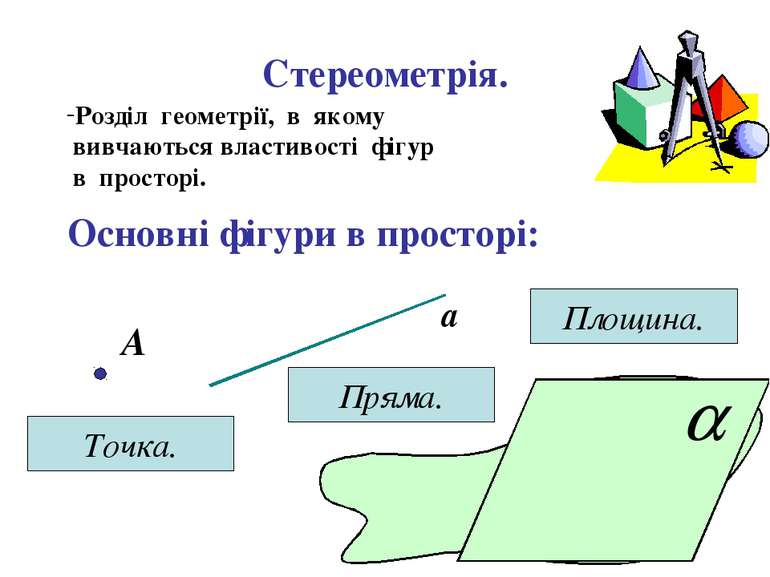
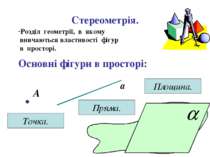
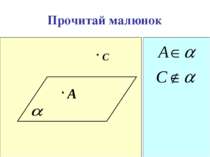
Стереометрія. Розділ геометрії, в якому вивчаються властивості фігур в просторі. Основні фігури в просторі: А Точка. а Пряма. Площина.

A, B, C, … a, b, c, … чи AВ, BС, CD, …

Геометричні тіла: Куб. Параллелепіпед. Тетраэдр.

Геометричні поняття. Площина – грань Пряма – ребро Точка – вершина вершина грань ребро

Аксіома (від греч. axíõma – поняття відносне) Поняття відносне наукової теорії, що приймається без доведення

АКСІОМИ планіметрія стереометрія 1. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй. 2. Через будь – які дві точки можна провести пряму і тільки одну. Властивості належності точок і прямих на площині: Властивість розміщення точок на прямій : 3. З трьох точок на прямій одна і тільки одна лежить між двома іншими. А1. Через будь – які три точки, що не лежать на одній прямій, можна провести площину, і до того ж тільки одну. А2. Якщо дві точки прямої лежать у площині, то і вся пряма лежить у цій площині. А3. Якщо дві площини мають спільну точку, то вони перетинаються по прямій, яка проходить через цю точку.

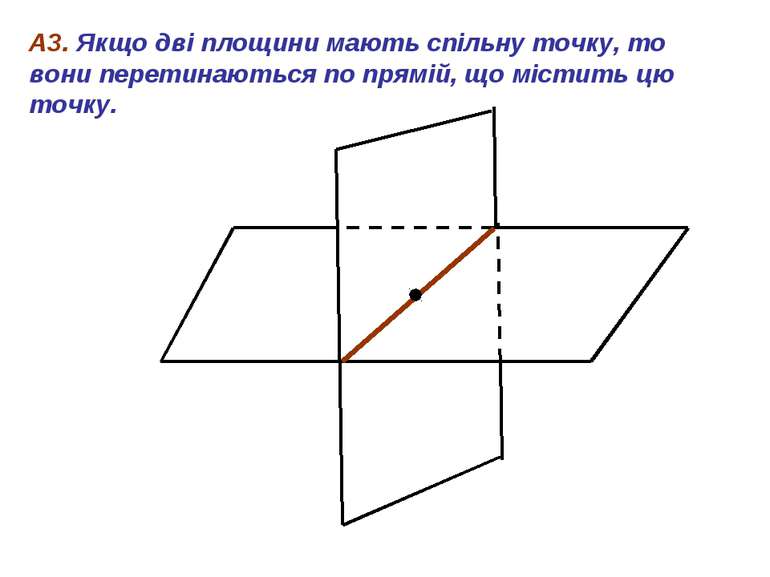
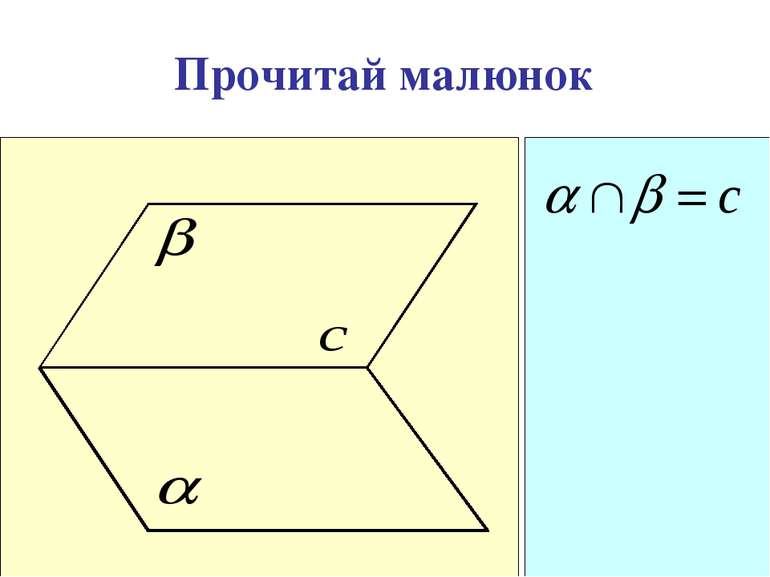
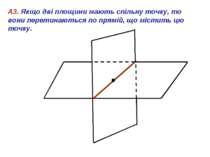
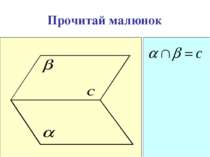
А3. Якщо дві площини мають спільну точку, то вони перетинаються по прямій, що містить цю точку.

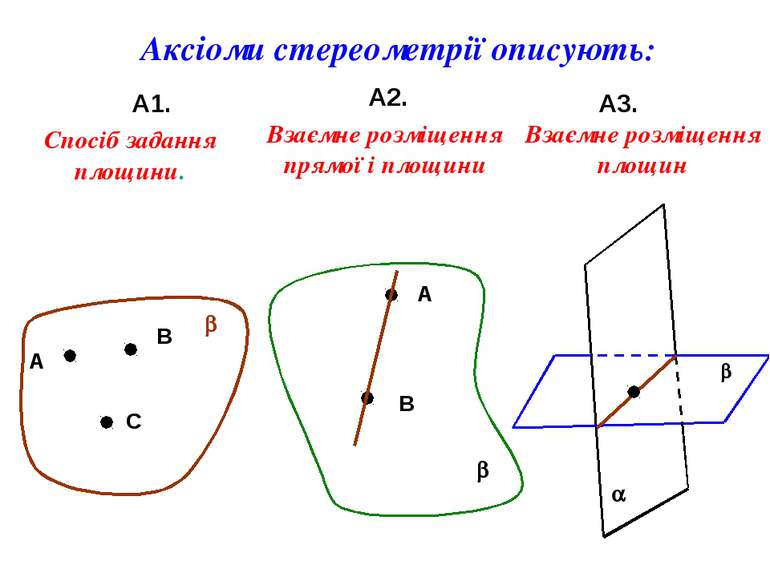
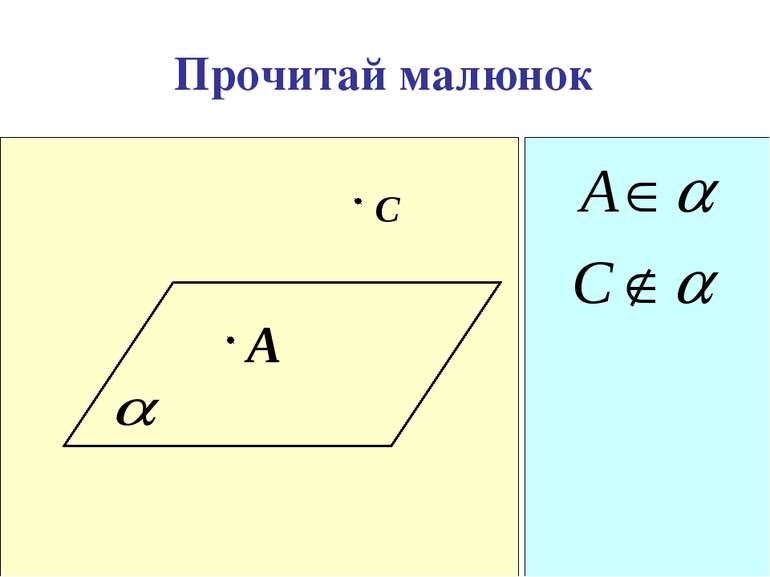
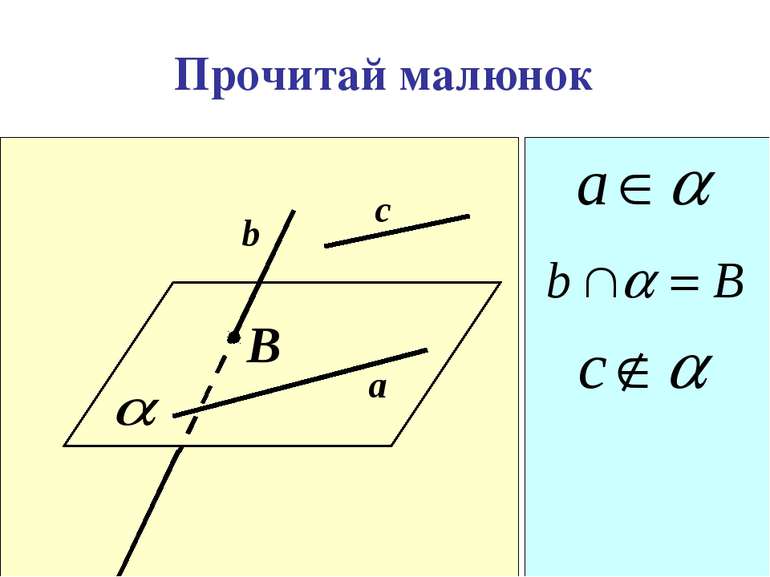
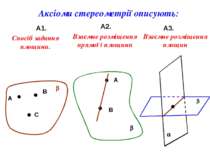
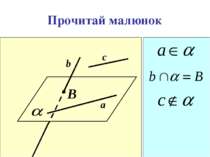
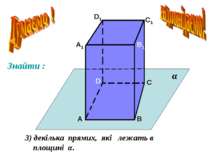
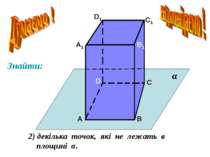
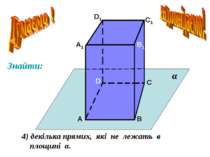
Аксіоми стереометрії описують: А1. А2. А3. А В С b Спосіб задання площини. b А В Взаємне розміщення прямої і площини a b Взаємне розміщення площин

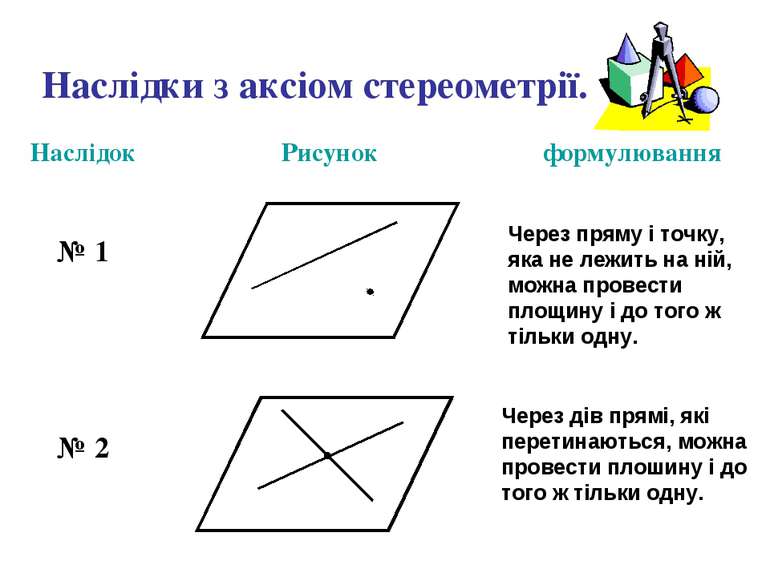
Наслідки з аксіом стереометрії. Через пряму і точку, яка не лежить на ній, можна провести площину і до того ж тільки одну. Через дів прямі, які перетинаються, можна провести плошину і до того ж тільки одну.

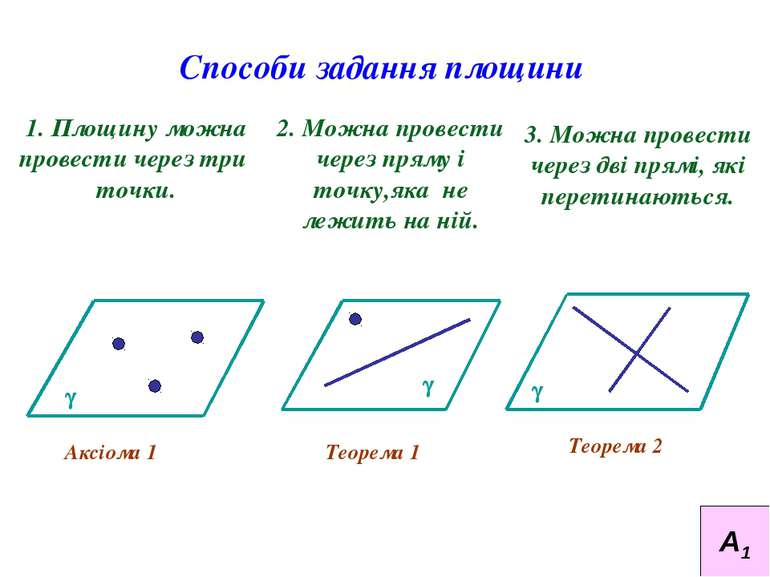
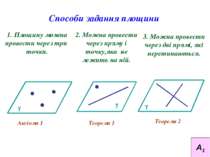
Способи задання площини 1. Площину можна провести через три точки. 2. Можна провести через пряму і точку,яка не лежить на ній. Аксіома 1 Теорема 1 Теорема 2 3. Можна провести через дві прямі, які перетинаються. А1

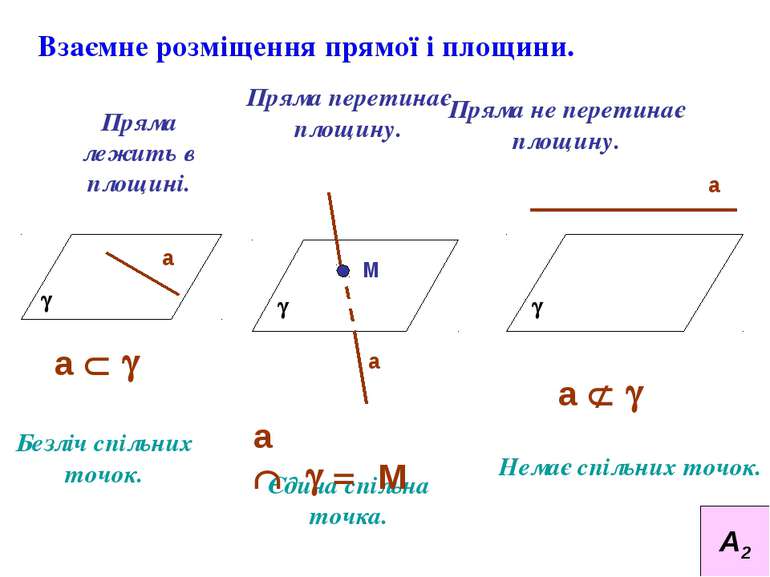
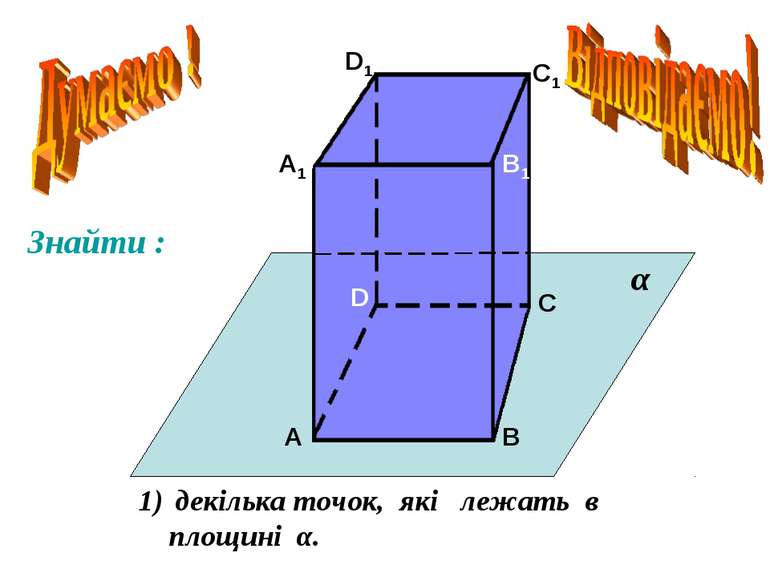
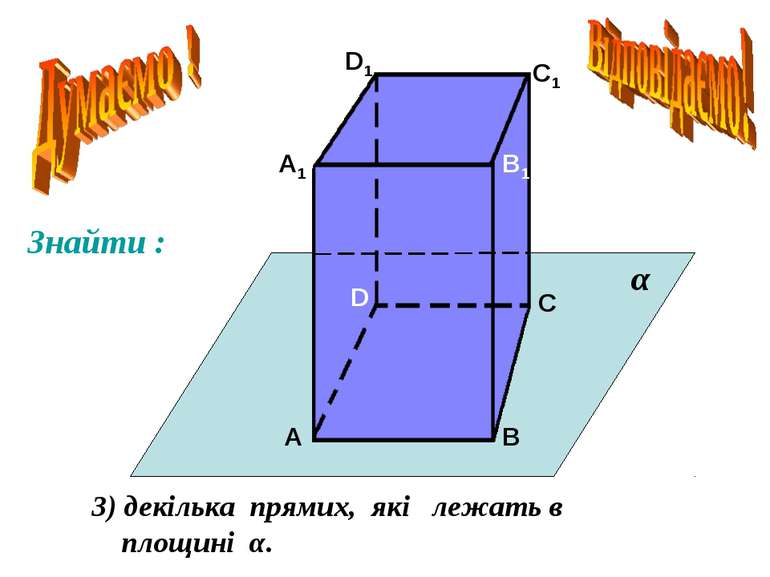
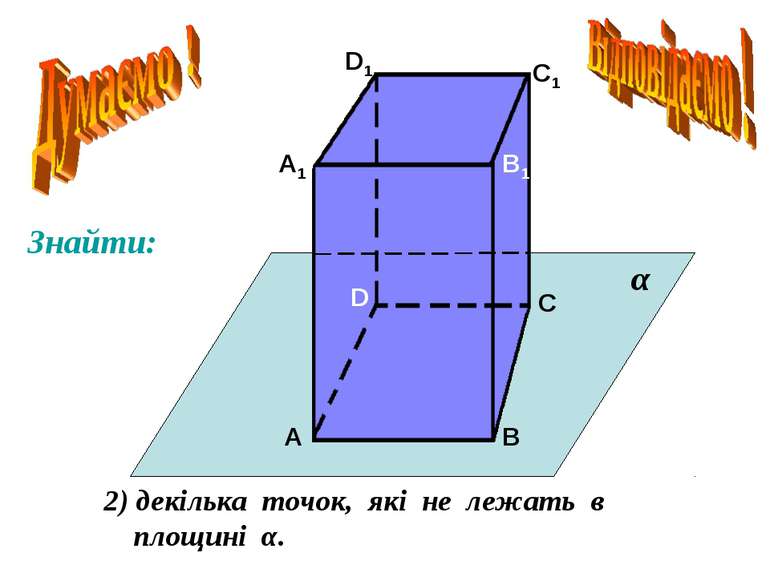
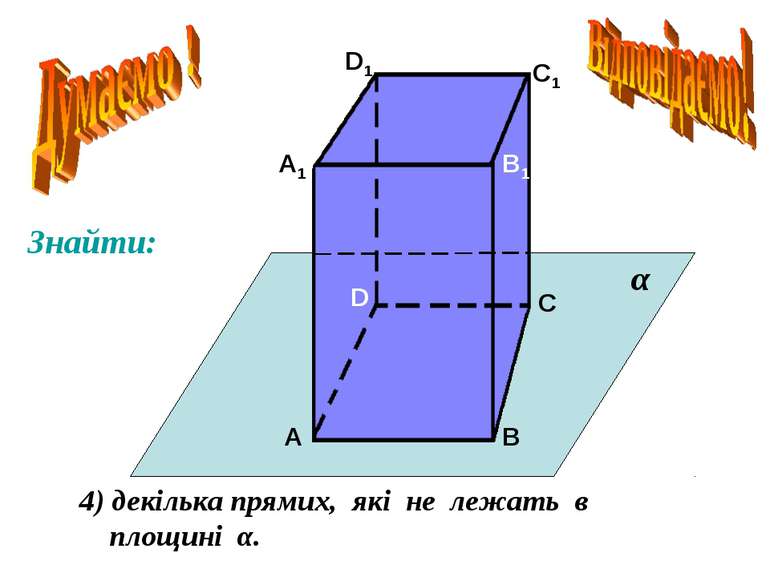
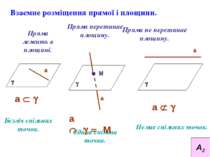
Взаємне розміщення прямої і площини. Пряма лежить в площині. Пряма перетинає площину. Пряма не перетинає площину. Безліч спільних точок. Єдина спільна точка. Немає спільних точок. g а g а М g а а Ì g а Ç g = М а Ë g А2

Прочитай малюнок A С

Прочитай малюнок B c b a

Прочитай малюнок

№ 2

А А1 В В1 С С1 D D1 декілька точок, які лежать в площині α. α Знайти :

А А1 В В1 С С1 D D1 3) декілька прямих, які лежать в площині α. α Знайти :

А А1 В В1 С С1 D D1 2) декілька точок, які не лежать в площині α. α Знайти:

А А1 В В1 С С1 D D1 4) декілька прямих, які не лежать в площині α. α Знайти:

А А1 В В1 С С1 D D1 5) декілька прямих, які перетинають пряму ВС α Знайти:

А А1 В В1 С С1 D D1 5) декілька прямих, які не перетинають пряму ВС. α Знайти:

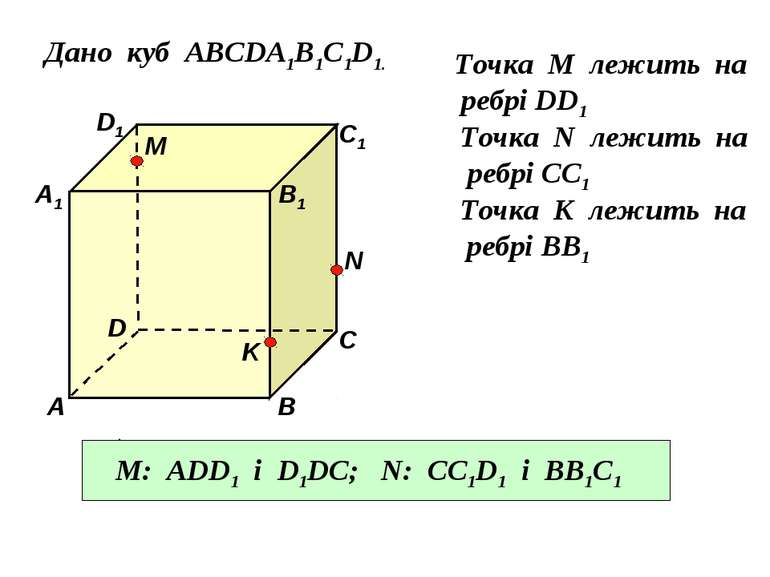
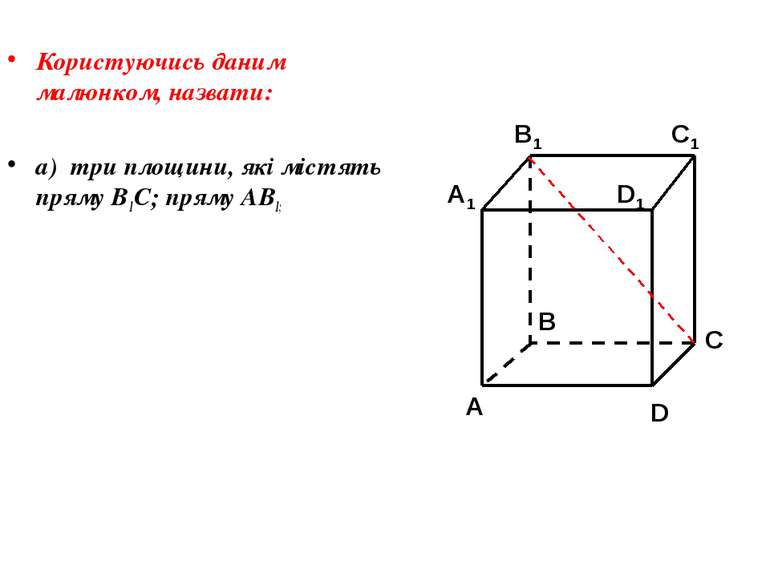
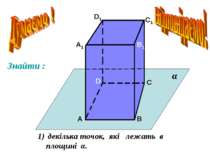
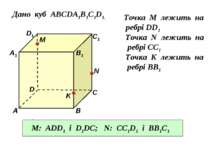
Дано куб АВСDA1B1C1D1. Точка М лежить на ребрі DD1 Точка N лежить на ребрі CC1 Точка K лежить на ребрі BB1 D1 В А1 А D С1 С В1 M N K Назвати площини в яких лежать точка М, точка N. M: ADD1 і D1DC; N: CC1D1 і BB1C1

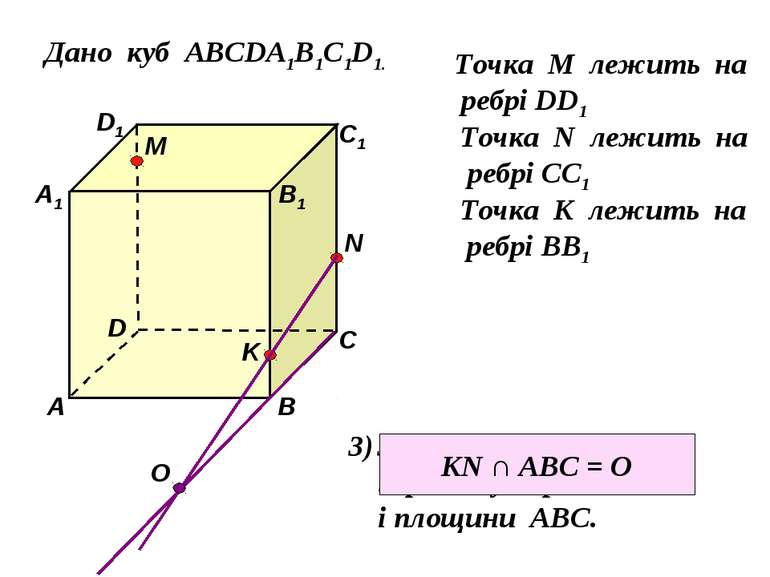
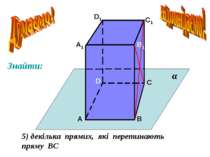
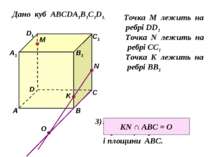
Дано куб АВСDA1B1C1D1. D1 D С1 С В1 В А1 А M Точка М лежить на ребрі DD1 N Точка N лежить на ребрі CC1 K Точка K лежить на ребрі BB1 Знайти точку перетину прямої KN і площини АВС. О KN ∩ ABC = O

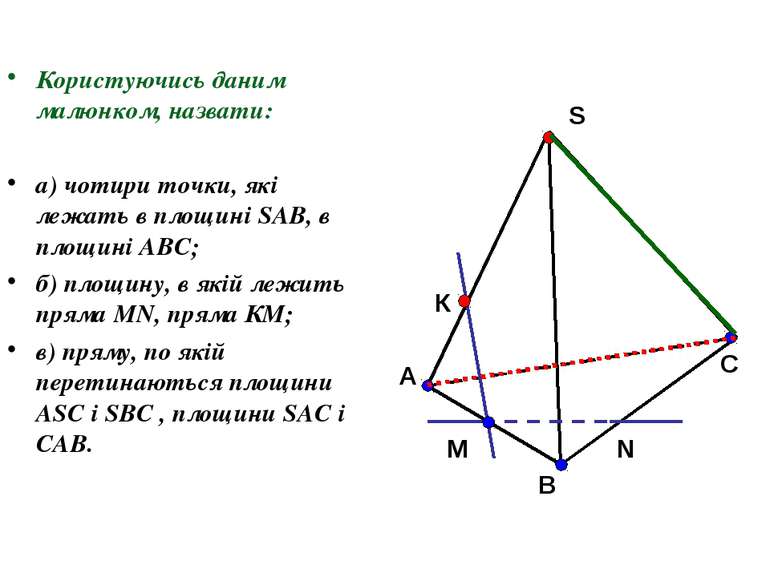
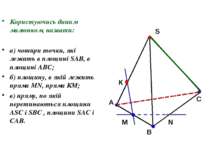
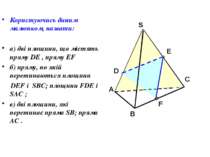
Користуючись даним малюнком, назвати: а) чотири точки, які лежать в площині SAB, в площині АВС; б) площину, в якій лежить пряма MN, пряма КМ; в) пряму, по якій перетинаються площини ASC і SBC , площини SAC і CAB.

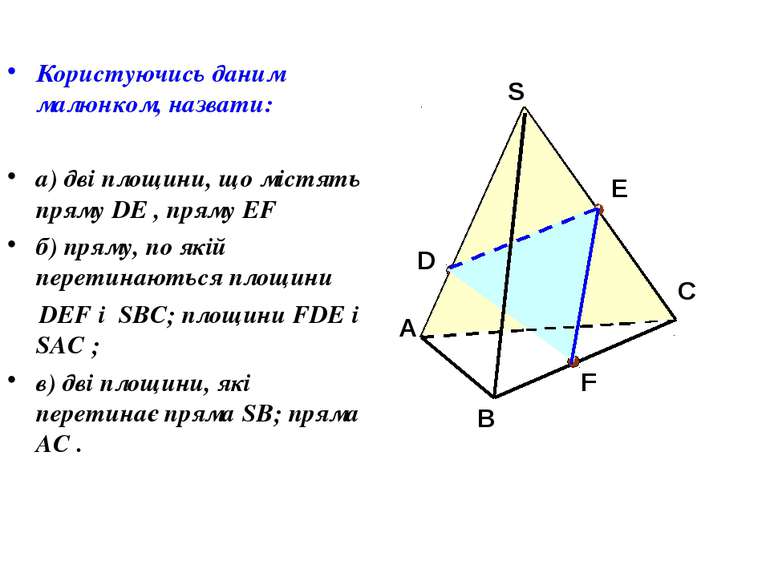
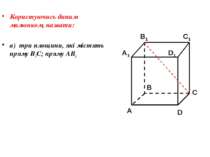
Користуючись даним малюнком, назвати: а) дві площини, що містять пряму DE , пряму EF б) пряму, по якій перетинаються площини DEF і SBC; площини FDE і SAC ; в) дві площини, які перетинає пряма SB; пряма AC .

Користуючись даним малюнком, назвати: а) три площини, які містять пряму В1С; пряму АВ1;

Закріплення вивченого матеріалу

Домашнє завдання: Вивчити аксіоми і наслідки з них. 2) П. 1-3 стр. 4 – 7. 3) №№ 4; 6; 10. Успіхів!