Презентація на тему:
ПОЧАТКОВІ ВІДОМОСТІ З СТЕРЕОМЕТРІЇ.

ПОЧАТКОВІ ВІДОМОСТІ З СТЕРЕОМЕТРІЇ.

ЛЮБІ ДЕВ’ЯТИКЛАСНИКИ ! Сьогодні ми з вами розпочинаємо роботу над проектом “ Початкові відомості стереометрії. Многогранники. Тіла обертання.” Під час роботи над даним проектом ми з вами розширимо свої знання про геометричні фігури, познайомимося із просторовими фігурами – тілами. “Тіло є те, що має довжину, ширину, глибину.” Евклід.

СТЕРЕОМЕТРІЯ- це розділ геометрії, у якому вивчаються фігури в просторі. Основні фігури стереометрії: точка, пряма, площина.

МЕТА ПРОЕКТУ: Вивчити означення та властивості призми. Вивчити означення та властивості піраміди. Вивчити означення та властивості тіл обертання. Розвивати просторову уяву, логічне мислення, пам’ять. Вчити учнів аналізувати, робити висновки. Показати можливість використання знань з даної теми при розв’язуванні задач практичного змісту. Виховувати в учнів інтерес до вивчення математики.

ЗАВДАННЯ ПРОЕКТУ: Ознайомитися з геометричними фігурами в просторі. Вивчити означення та властивості цих фігур. Навчитися розв’язувати задачі на знаходження площі повної, бічної поверхні та об’єму призми, піраміди, циліндра, конуса, кулі. Підібрати цікаву інформацію про застосування властивостей даних геометричних фігур у житті.

МНОГОГРАННИКИ. ПРИЗМА. Многогранником називають геометричне тіло обмежене скінченою кількістю плоских многокутників. Призмою називається многогранник, який складається з двох плоских многокутників, які лежать в різних площинах і суміщаються паралельним перенесенням, і всіх відрізків, які з’єднують відповідні точки цих мнонгокутників. Призма називається прямою, якщо її бічні ребра перпендикулярні основам.

Просторові геометричні фігури – многогранники. Піраміда Призма Октаедр Додекаедр Ікосаедр

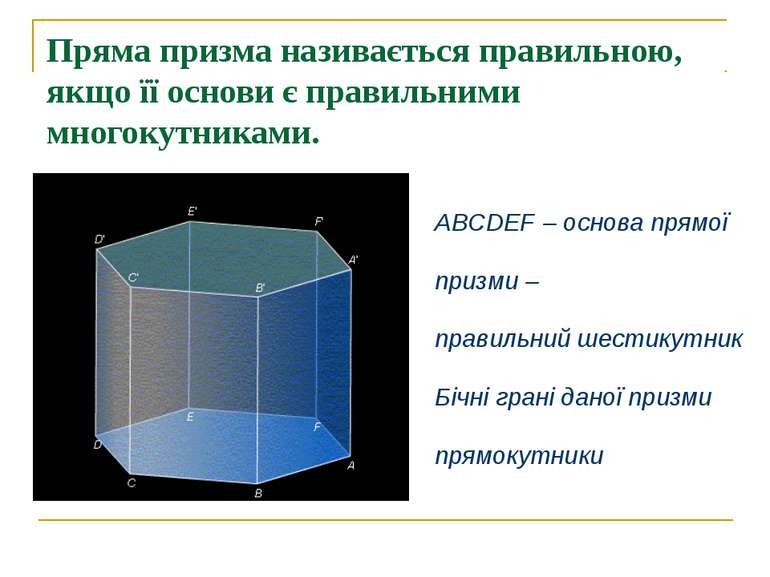
Пряма призма називається правильною, якщо її основи є правильними многокутниками. ABCDEF – основа прямої призми – правильний шестикутник Бічні грані даної призми прямокутники

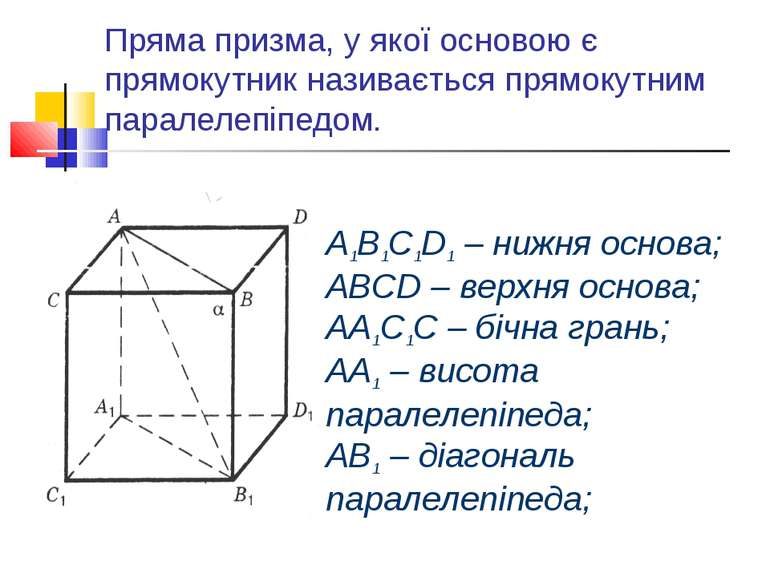
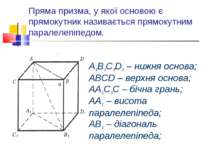
Пряма призма, у якої основою є прямокутник називається прямокутним паралелепіпедом. А1В1С1D1 – нижня основа; АВСD – верхня основа; АА1С1С – бічна грань; АА1 – висота паралелепіпеда; АВ1 – діагональ паралелепіпеда;

Кубом називається прямокутний паралелепіпед, у якого всі ребра рівні. Куб складається із шести граней, кожна з яких є квадратом. Sосн. = а2 Sповн.пов. = 6а2 V = а3

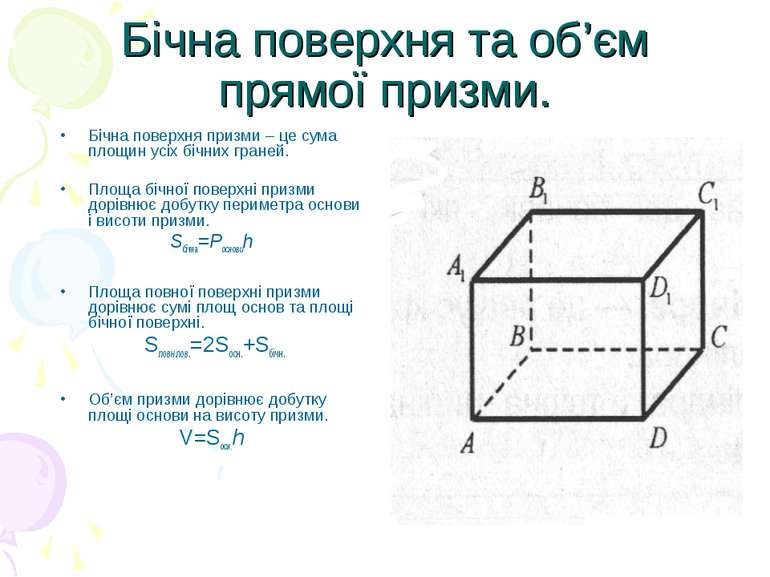
Бічна поверхня та об’єм прямої призми. Бічна поверхня призми – це сума площин усіх бічних граней. Площа бічної поверхні призми дорівнює добутку периметра основи і висоти призми. Sбічна=Pосновиh Площа повної поверхні призми дорівнює сумі площ основ та площі бічної поверхні. Sповн.пов.=2Sосн.+Sбічн. Об’єм призми дорівнює добутку площі основи на висоту призми. V=Sосн.h

Розв’яжіть задачі. 1.Основою прямої трикутної призми є прямокутний трикутник з катетами 0,7см і 2,4см, бічне ребро призми рівне 10см. Знайдіть площу бічної поверхні призми. 2. Основою прямої призми є прямокутник, сторони якого дорівнюють 8см і 6см. Бічне ребро дорівнює 10см. Обчисліть об’єм призми.

ПІРАМІДА. Пірамідою називається многогранник, який складається з плоского многокутника, точки, яка не лежить в площині основи, та всіх відрізків, які з’єднують вершину піраміди з точками основи.

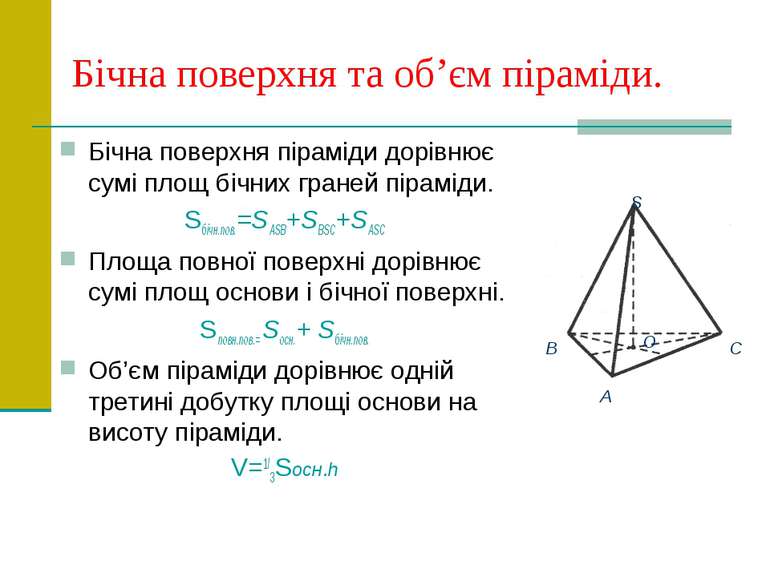
Бічна поверхня та об’єм піраміди. Бічна поверхня піраміди дорівнює сумі площ бічних граней піраміди. Sбічн.пов.=SASB+SBSC+SASC Площа повної поверхні дорівнює сумі площ основи і бічної поверхні. Sповн.пов.= Sосн.+ Sбічн.пов. Об’єм піраміди дорівнює одній третині добутку площі основи на висоту піраміди. V=1/3Sосн.h S A B C O

Розв’яжіть задачі. 3.В основі піраміди лежить прямокутний трикутник з катетами 3см і 4см. Обчисліть об’єм піраміди, якщо висота дорівнює 5см. 4. В основі піраміди лежить квадрат АВСД зі стороною 10см. Висота бічної грані піраміди рівна 12см. Знайдіть площу поверхні піраміди.

ТІЛА ОБЕРТАННЯ. Циліндр Конус Куля

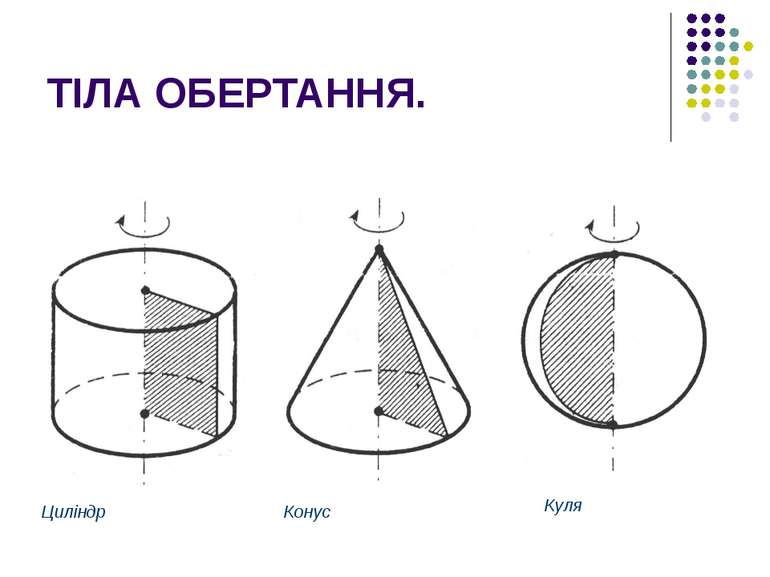
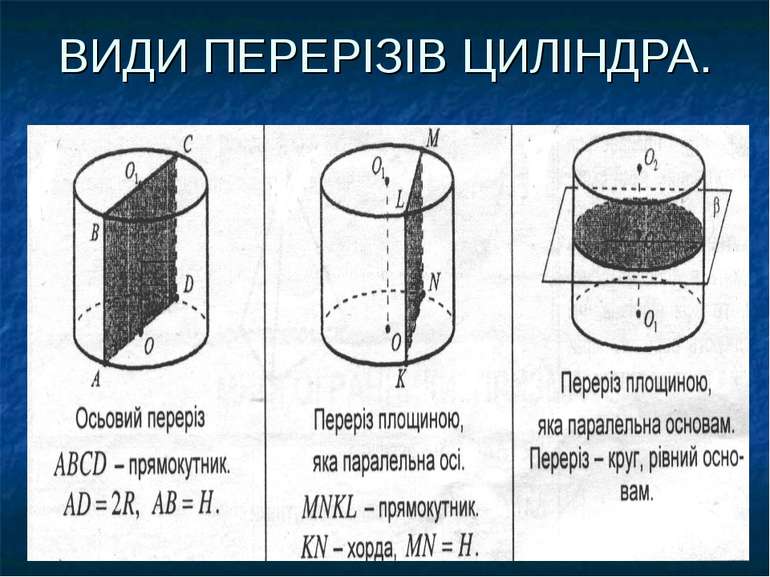
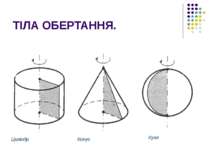
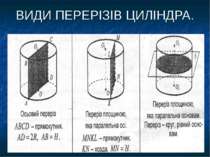
ТІЛА ОБЕРТАННЯ. ЦИЛІНДР. Циліндром називається тіло, яке складається із двох кругів, що не лежать в одній площині і суміщаються паралельним перенесенням, і всіх відрізків, що з’єднують відповідні точки цих кругів. Основи – рівні круги. Твірні є висотами циліндра. Циліндр утворюється в результаті обертання прямокутника навколо однієї із сторін цього прямокутника.

ВИДИ ПЕРЕРІЗІВ ЦИЛІНДРА.

ЦИЛІНДР. Sбічн.=2ПRh Sосн. = ПR2 Sповн.пов=2ПRh+2ПR2 V= ПR2H R – радіус основи h – висота циліндра П = 3,14...

Розв’яжіть задачі. 5. Знайдіть площу бічної поверхні циліндра з радіусом основи 2см і висотою 5см. 6. Знайдіть площу повної поверхні циліндра з радіусом основи 3см і висотою 4см. ( Відповідь округліть до десятих )

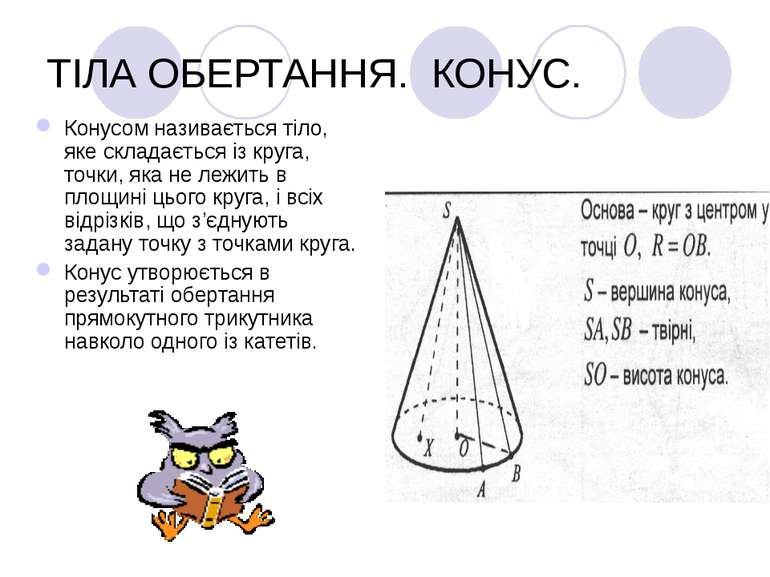
ТІЛА ОБЕРТАННЯ. КОНУС. Конусом називається тіло, яке складається із круга, точки, яка не лежить в площині цього круга, і всіх відрізків, що з’єднують задану точку з точками круга. Конус утворюється в результаті обертання прямокутного трикутника навколо одного із катетів.

ВИДИ ПЕРЕРІЗІВ КОНУСА.

КОНУС. Sосн.= ПR2 Sбічн.= ПRL Sповн.пов. = Sосн.+ Sбічн Sповн.пов = ПR2 + ПRL V = 1/3 ПR2H R – радіус основи L – твірна конуса H – висота конуса

Розв’яжіть задачі. 7. Знайдіть об’єм конуса з радіусом 3см і висотою 8см. 8. Знайдіть площу повної поверхні конуса з діаметром основи 6см і твірною 5см.

КУЛЯ. Кулею називається тіло, яке складається з усіх точок простору, що знаходяться на відстані, не більшій даної, від даної точки. Задана відстань – це радіус кулі. Задана точка – це центр кулі. Куля утворюється при обертанні півкруга навколо свого діаметра.

КУЛЯ. Площа поверхні кулі Sповерхні =4ПR2. Об’єм кулі V=4/3ПR3. П = 3,14.. R - радіус кулі

Розв’яжіть задачі. 9. Знайдіть площу поверхні кулі радіусом 8см. 10. Знайдіть об’єм кулі, якщо радіус кулі дорівнює 3см.

Домашнє завдання