Презентація на тему:
Початкові відомості зі стереометрії

Початкові відомості стереометрії 9клас

Світ просторових фігур є відтворенням навколишнього світу, в якому ми живемо.

ІСТОРИЧНА ДОВІДКА Стереометрія як розділ геометрії зароджувалася і розвивалася одночасно з планіметрією. Майже всі твердження про паралельність і перпендикулярність прямих і площин у просторі були відомі в Давній Греції, чимало з них викладені у «Началах» Евкліда.

Властивості многогранників і тіл обертання першими систематично виклали давньогрецькі математики. Окрім Евкліда, слід особливо виділити Архімеда, який у двох своїх працях дослідив властивості тіл обертання.

Одним із засновників теорії конічних поверхонь вважається давньогрецький геометр Аполлоній Пергський (бл. 262 - бл. 190 p.p. до н. е.)

Важливі дослідження в галузі геометрії многогранників належать всесвітньо відомому українському математикові Георгію Феодосійовичу Вороному (1868-1908). Зокрема, він дослідив проблему заповнення простору рівними опуклими многогранниками.

Об'єми деяких многогранників уміли обчислювати ще в Стародавньому Єгипті. Значною мірою сприяли вдосконаленню методів обчислень об'ємів роботи італійського математика Бонавентури Кавальєрі (1598-1647), який установив ознаку тіл, що мають рівні об'єми, нині відому як принцип Кавальєрі. Але строга сучасна теорія об'ємів, заснована на методах математичного аналізу, з'явилася значно пізніше.

Стереометрія — від грецького «стерео» — тіло і «метрео» — вимірюю — вимірювання тіл

Cтереометрія є математичною наукою і вивчає фігури абстрактно. Проте основою такого абстрагування є реальний світ.

Слово сфера походить від грецького «м'яч»; куб - від «гральна кістка»; циліндр - від «коток»; призма - від «розпиляна»; конус – від «соснова шишки», «кегля», «верхівка шолома»; пірамідою стародавні єгиптяни називали свої споруди – гробниці фараонів

Прямі і площини в просторі

Основними фігурами в просторі є точка, пряма і площина α α A

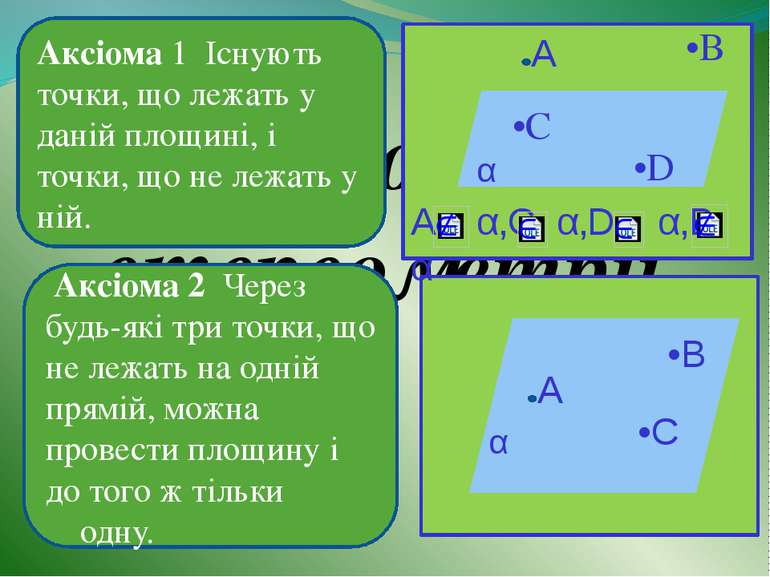
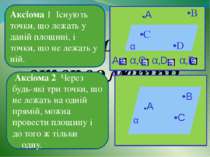
Аксіоми стереометрії Аксіома 1 Існують точки, що лежать у даній площині, і точки, що не лежать у ній. Аксіома 2 Через будь-які три точки, що не лежать на одній прямій, можна провести площину і до того ж тільки одну. •В •С •D α А A α‚C α‚D α‚B α α •В •C

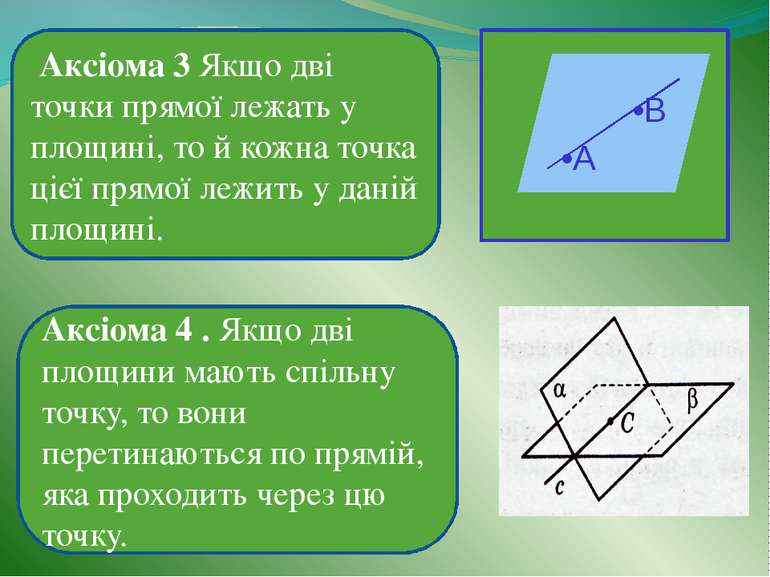
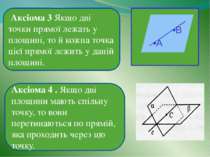
Аксіома 3 Якщо дві точки прямої лежать у площині, то й кожна точка цієї прямої лежить у даній площині. Аксіома 4 . Якщо дві площини мають спільну точку, то вони перетинаються по прямій, яка проходить через цю точку. •A •B

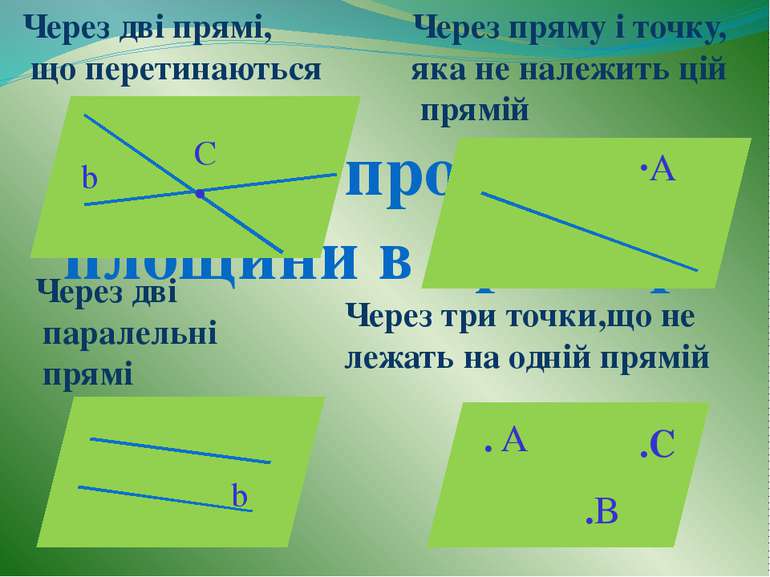
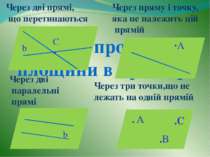
Способи проведення площини в просторі β β β α ·А b β α C • α b . A .B .C Через дві прямі, що перетинаються Через пряму і точку, яка не належить цій прямій Через дві паралельні прямі Через три точки,що не лежать на одній прямій

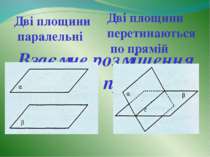
Взаємне розміщення прямої і площини в просторі Пряма лежить у площині Пряма перетинає площину Пряма паралельна площині α β β α α β

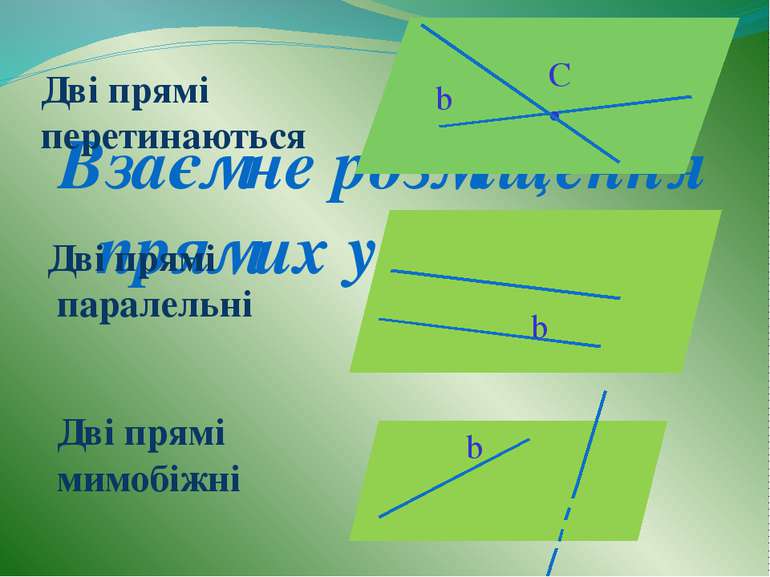
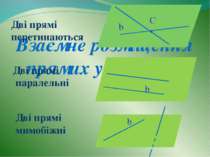
Взаємне розміщення прямих у просторі Дві прямі перетинаються Дві прямі паралельні Дві прямі мимобіжні b C • β β α b β α b α

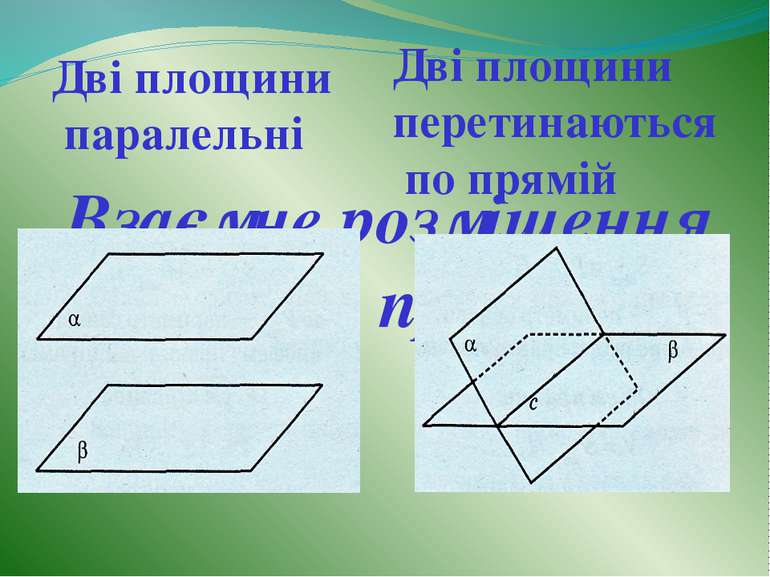
Взаємне розміщення площин у просторі Дві площини паралельні Дві площини перетинаються по прямій

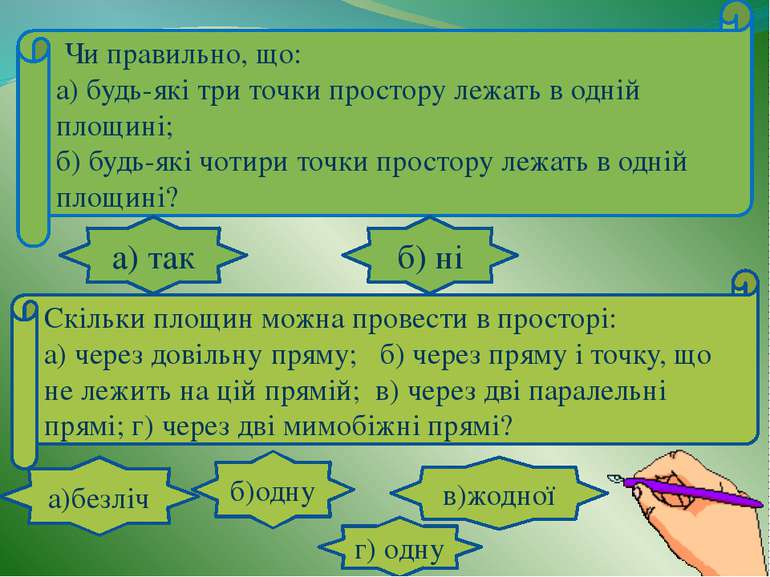
Чи правильно, що: а) будь-які три точки простору лежать в одній площині; б) будь-які чотири точки простору лежать в одній площині? а) так б) ні Скільки площин можна провести в просторі: а) через довільну пряму; б) через пряму і точку, що не лежить на цій прямій; в) через дві паралельні прямі; г) через дві мимобіжні прямі? а)безліч б)одну г) одну в)жодної

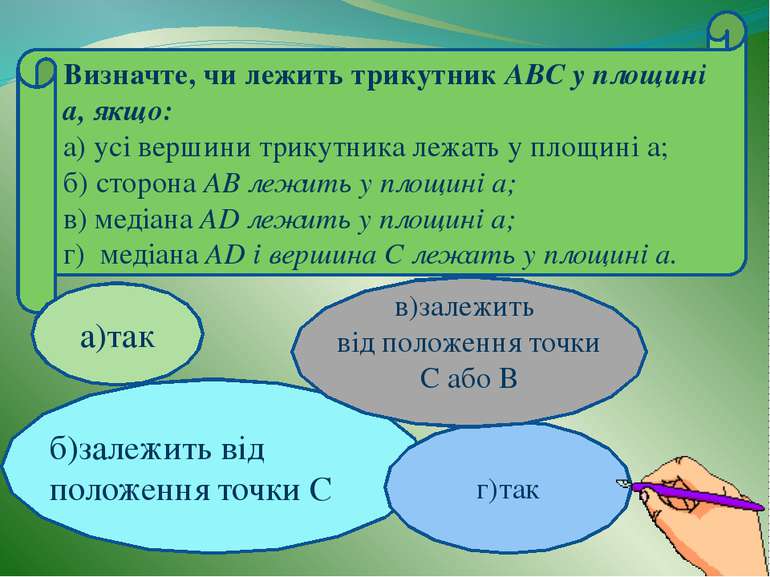
Визначте, чи лежить трикутник ABC у площині а, якщо: а) усі вершини трикутника лежать у площині а; б) сторона АВ лежить у площині а; в) медіана AD лежить у площині а; г) медіана АD і вершина С лежать у площині а. а)так б)залежить від положення точки С г)так в)залежить від положення точки С або В

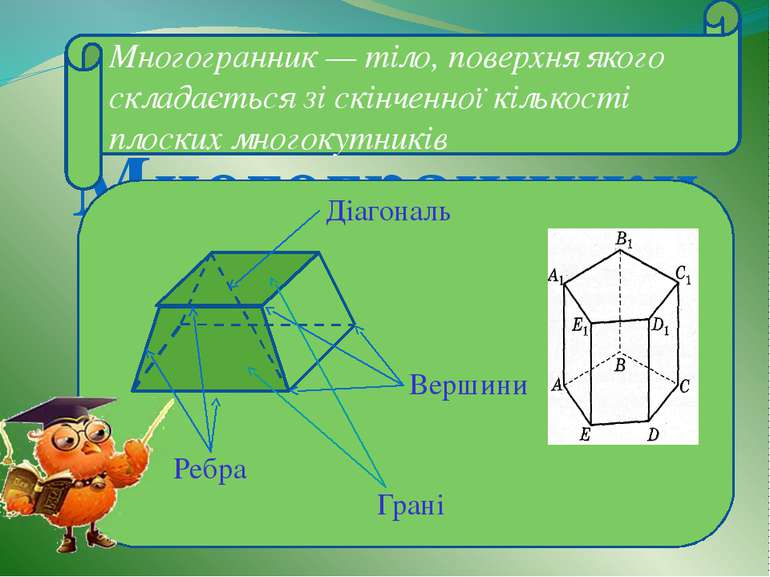
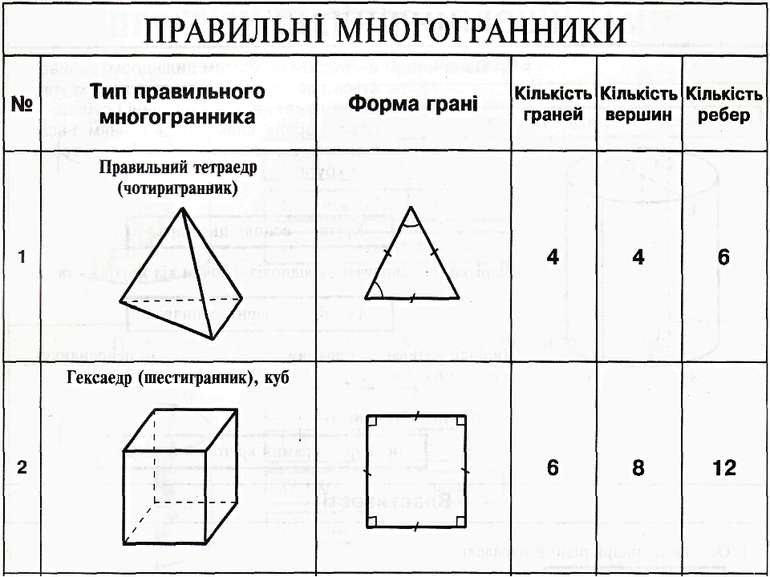
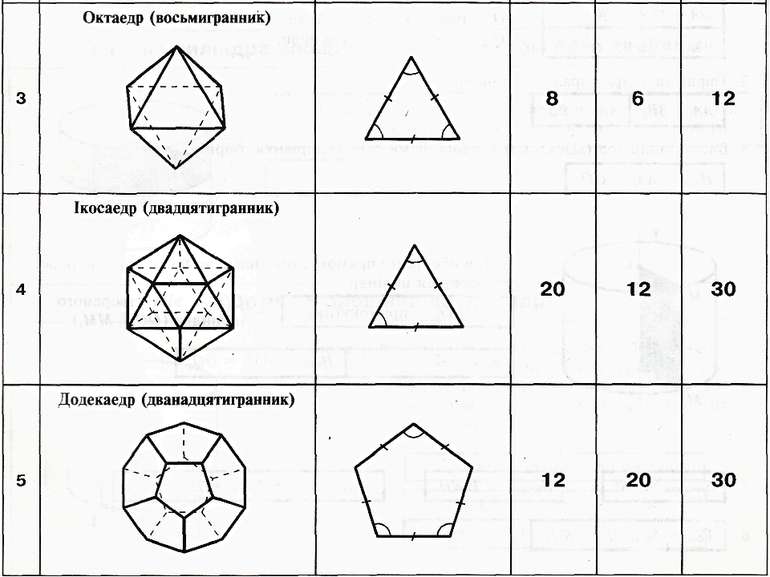
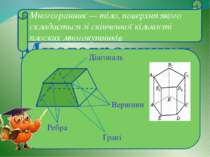
Многогранники Многогранник — тіло, поверхня якого складається зі скінченної кількості плоских многокутників Діагональ Вершини Ребра Грані

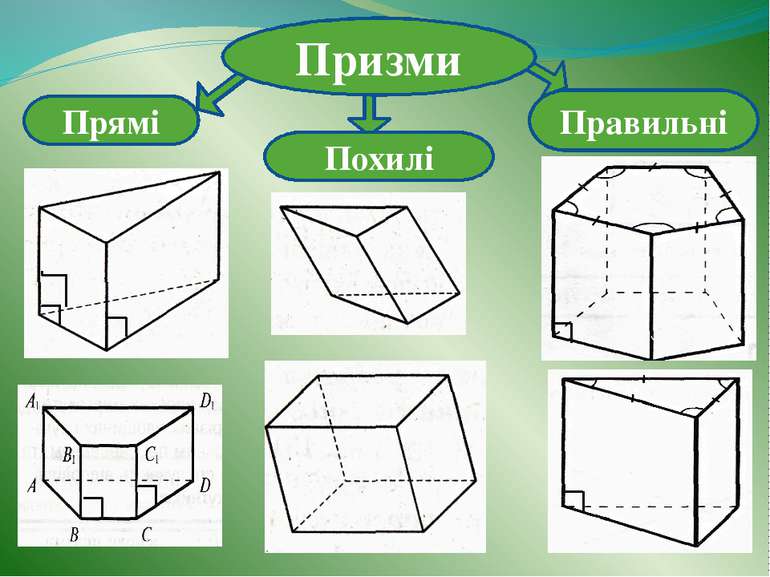
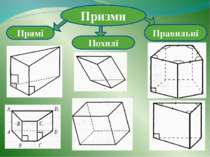
паралельним перенесенням, і всіх відрізків, що сполучають відповідні точки цих многокутників називають призмою. Многогранник, поверхня якого складається з двох плоских многокутників, що лежать у різних площинах і суміщаються

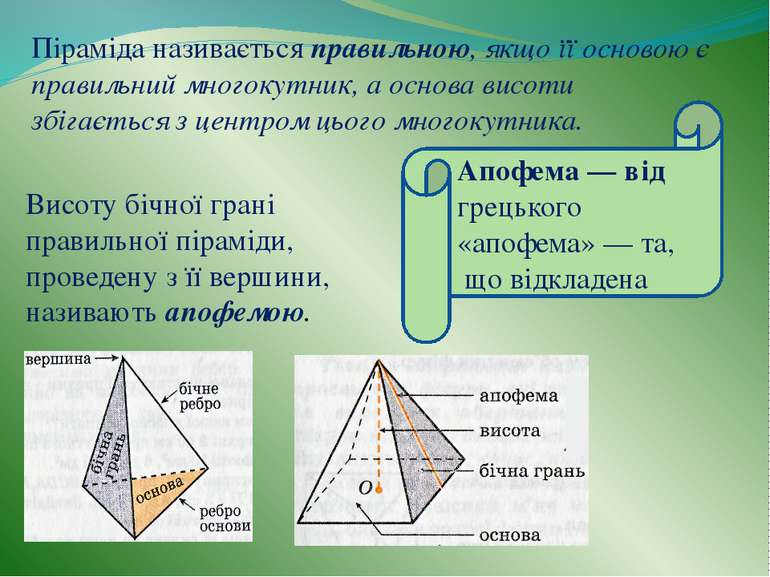
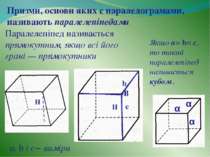
Плоскі многокутники називають основами, інші грані — бічними гранями, а ребра призми, що сполучають відповідні вершини основ,— бічними ребрами призми.

Призми Прямі Похилі Правильні

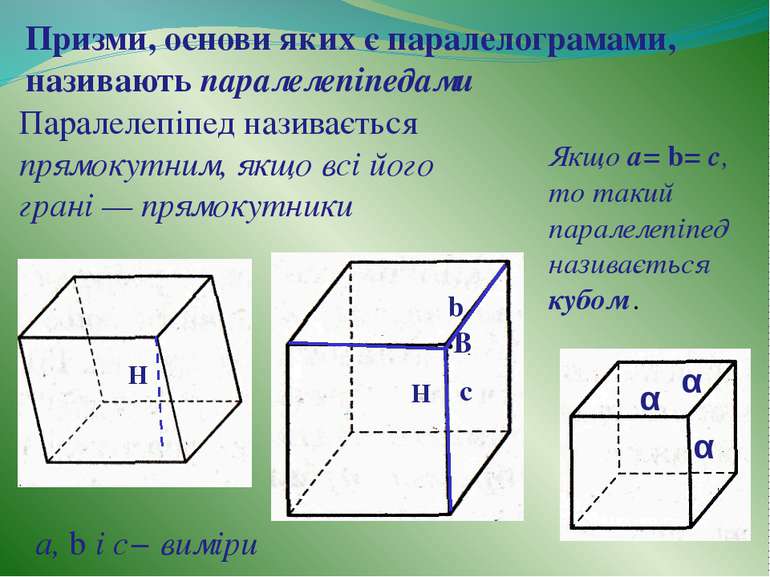
Якщо а= b= с, то такий паралелепіпед називається кубом . Призми, основи яких є паралелограмами, називають паралелепіпедами Паралелепіпед називається прямокутним, якщо всі його грані — прямокутники α b c •В а, b і с− виміри Н Н α α α

Основні формули для призм Площа бічної поверхні прямої призми Sбічн =Росн ·Н де Росн — периметр основи, Н — бічне ребро прямої призми Об'єм призми V= Sосн ·Н де Sосн— площа основи, Н —висота призми Площа повної поверхні прямої призми Sпов = Sбічн +2Sосн Sпов = Росн ·Н +2Sосн

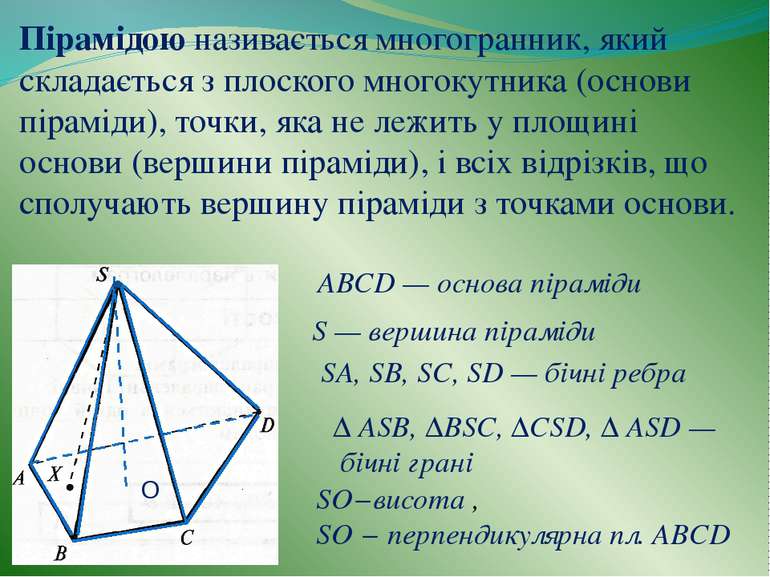
Пірамідою називається многогранник, який складається з плоского многокутника (основи піраміди), точки, яка не лежить у площині основи (вершини піраміди), і всіх відрізків, що сполучають вершину піраміди з точками основи. ABCD — основа піраміди S — вершина піраміди SA, SB, SC, SD — бічні ребра ∆ ASB, ∆BSC, ∆CSD, ∆ ASD — бічні грані SО−висота , SO − перпендикулярна пл. ABCD О

Слово «піраміда» має грецьке походження, а спорудженням величних пірамід уславилися давні єгиптяни

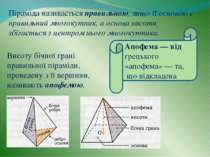
Висоту бічної грані правильної піраміди, проведену з її вершини, називають апофемою. Піраміда називається правильною, якщо її основою є правильний многокутник, а основа висоти збігається з центром цього многокутника. Апофема — від грецького «апофема» — та, що відкладена

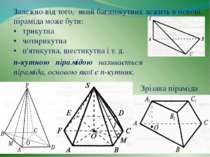
Залежно від того, який багатокутник лежить в основі, піраміда може бути: • трикутна • чотирикутна • п'ятикутна, шестикутна і т. д. п-кутною пірамідою називається піраміда, основою якої є п-кутник. Зрізана піраміда

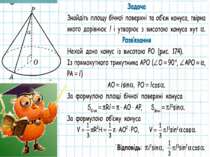
Основні формули для пірамід Площа бічної поверхні правильної піраміди Sбічн =½Росн ·l де Росн − периметр основи, l−апофема правильної піраміди Об'єм піраміди V= ¹⁄₃Sосн ·Н де Sосн−площа основи, Н − висота піраміди Площа повної поверхні правильної піраміди Sпов = Sбічн +Sосн Sпов = =½Росн ·l +Sосн

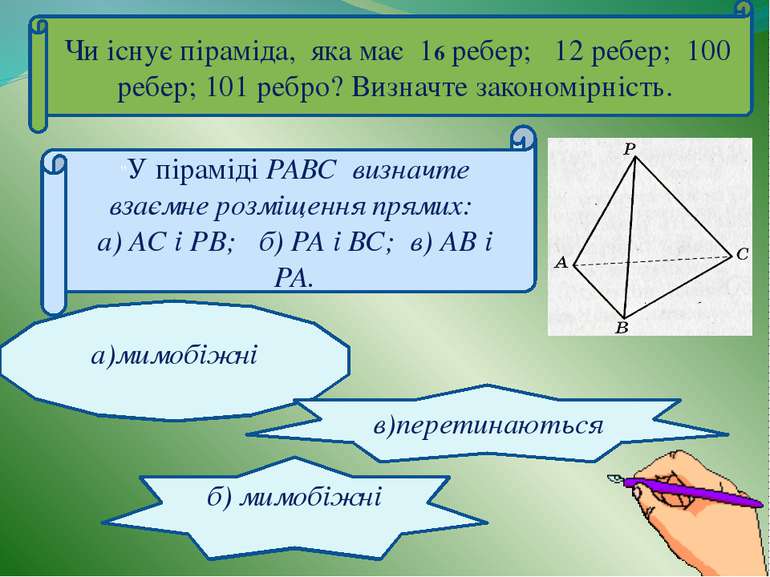
Чи існує піраміда, яка має 16 ребер; 12 ребер; 100 ребер; 101 ребро? Визначте закономірність. а)мимобіжні "У піраміді РАВС визначте взаємне розміщення прямих: а) АС і РВ; б) РА і ВС; в) АВ і РА. б) мимобіжні в)перетинаються

Тіла обертання

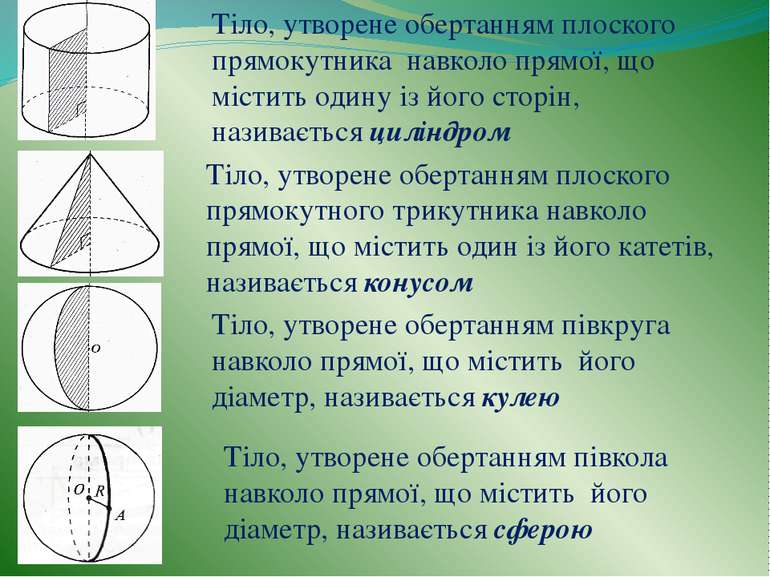
Тіло, утворене обертанням плоского прямокутника навколо прямої, що містить одину із його сторін, називається циліндром Тіло, утворене обертанням плоского прямокутного трикутника навколо прямої, що містить один із його катетів, називається конусом Тіло, утворене обертанням півкруга навколо прямої, що містить його діаметр, називається кулею Тіло, утворене обертанням півкола навколо прямої, що містить його діаметр, називається сферою

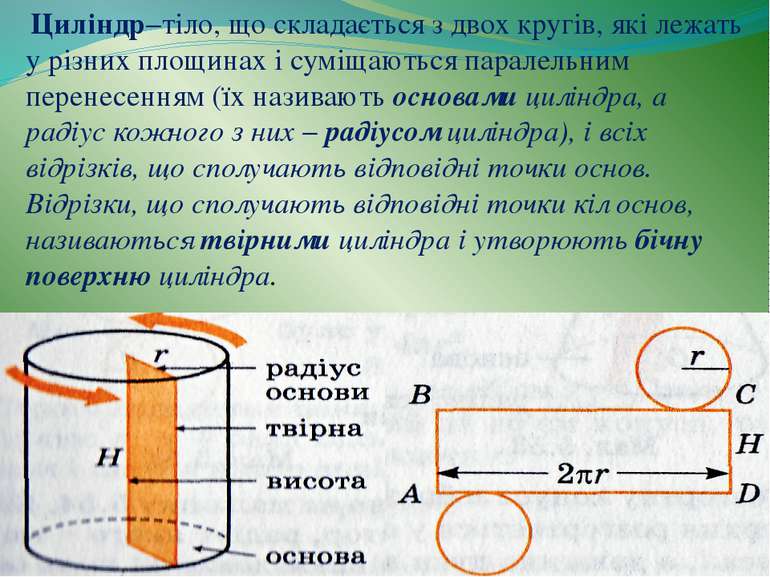
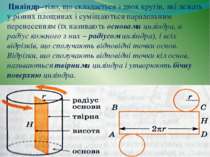
Циліндр−тіло, що складається з двох кругів, які лежать у різних площинах і суміщаються паралельним перенесенням (їх називають основами циліндра, а радіус кожного з них − радіусом циліндра), і всіх відрізків, що сполучають відповідні точки основ. Відрізки, що сполучають відповідні точки кіл основ, називаються твірними циліндра і утворюють бічну поверхню циліндра.

Основні формули для циліндрів Площа бічної поверхні циліндра Sбічн =2πRН де R−радіус основи, Н −висота Об'єм призми V= π R²Н де R−радіус основи, Н −висота Площа повної поверхні циліндра Sпов = Sбічн +2Sосн Sпов = 2πRН+2πR²= 2πR(R+Н)

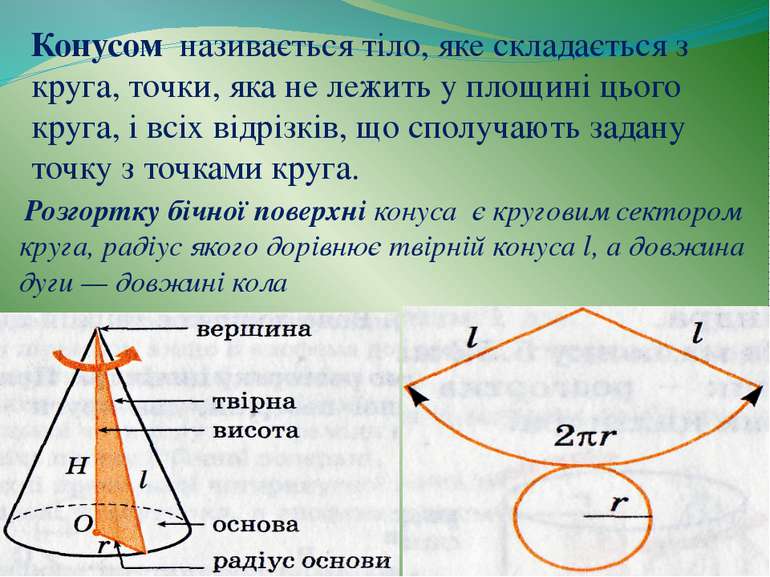
Конусом називається тіло, яке складається з круга, точки, яка не лежить у площині цього круга, і всіх відрізків, що сполучають задану точку з точками круга. Розгортку бічної поверхні конуса є круговим сектором круга, радіус якого дорівнює твірній конуса l, а довжина дуги — довжині кола

Основні формули для конусів Площа бічної поверхні конуса Sбічн =π Rl де R−радіус основи конуса, l −твірна конуса Об'єм конуса V=¹⁄₃Sосн·Н=¹⁄₃ πR²Н де Sосн−площа основи, Н − висота конуса, R−радіус основи конуса Площа повної поверхні конуса Sпов = Sбічн +Sосн Sпов =πRl+πR²=πR(l+R)

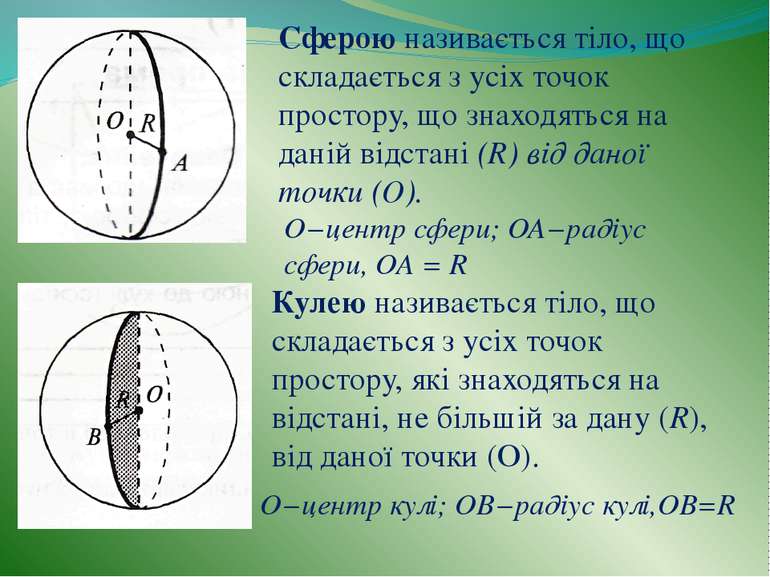
Сферою називається тіло, що складається з усіх точок простору, що знаходяться на даній відстані (R) від даної точки (О). Кулею називається тіло, що складається з усіх точок простору, які знаходяться на відстані, не більшій за дану (R), від даної точки (О). О−центр сфери; ОА−радіус сфери, ОА = R О−центр кулі; ОВ−радіус кулі,OB=R

Основні формули для кулі Площа сфери Sбічн =4πR² де R−радіус сфери Об'єм кулі V= πR³ де R−радіус кулі

Для допитливих Автомобільна покришка має тороїдальну форму. Пончики також мають тороїдальну форму.М'яч для гри в регбі за формою близький до еліпсоїда

Зауваження. Радіус земної кулі дорівнює приблизно 6400 км. Уявімо, що земну кулю вздовж екватора щільно обв'язали шнуром. Потім довжину цього шнура збільшили на 1 м так, що він по всій своїй довжині рівновіддалений від поверхні Землі. Чи може в утворений простір під шнуром пролізти миша? А тепер, збільшивши довжину шнура, як і в попередній задачі, в якомусь місці екватора «відтягнемо» шнур намаксимально можливу відстань від поверхні Землі.Чи зможе тепер під шнуром пройти слон?

Найбільше математика корисна тим, що безпосередньо сприяє розвиткові чіткого мислення і духу відкриття. Й. Ф. Гербарт

Бажаю успіхів!