Презентація на тему:
Аксіоми стереометрії. Деякі наслідки з них

Аксіоми стереометрії. Деякі наслідки

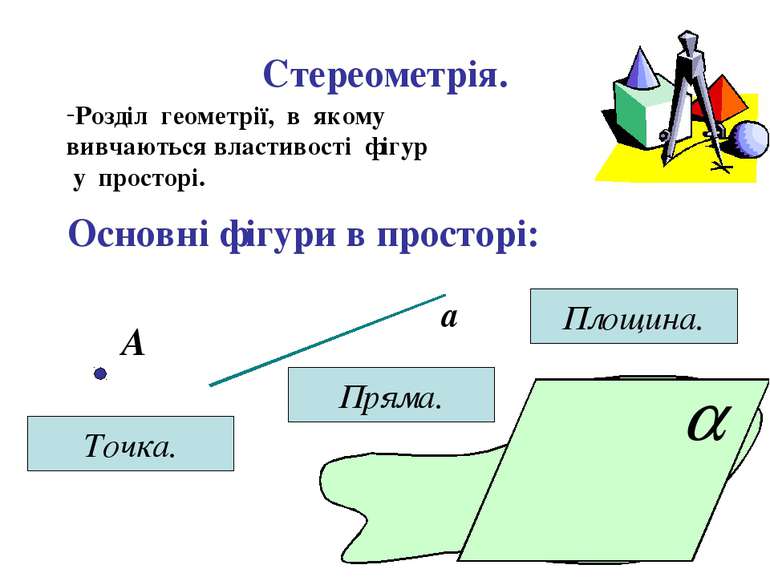
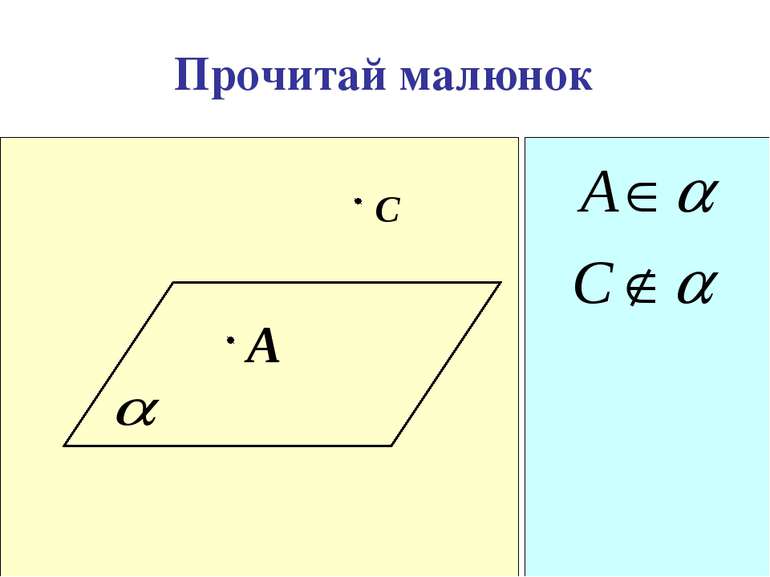
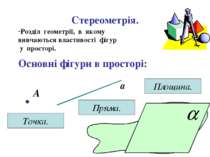
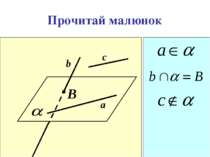
Стереометрія. Розділ геометрії, в якому вивчаються властивості фігур у просторі. Основні фігури в просторі: А Точка. а Пряма. Площина.

A, B, C, … a, b, c, … или AВ, BС, CD, …

Геометричні тіла: Куб. Паралелепіпед. Тетраєдр.

Геометричні поняття. Площина – грань Пряма – ребро Точка – вершина вершина грань ребро

Аксіома Початкове положення наукової теорії, що приймається без доведення

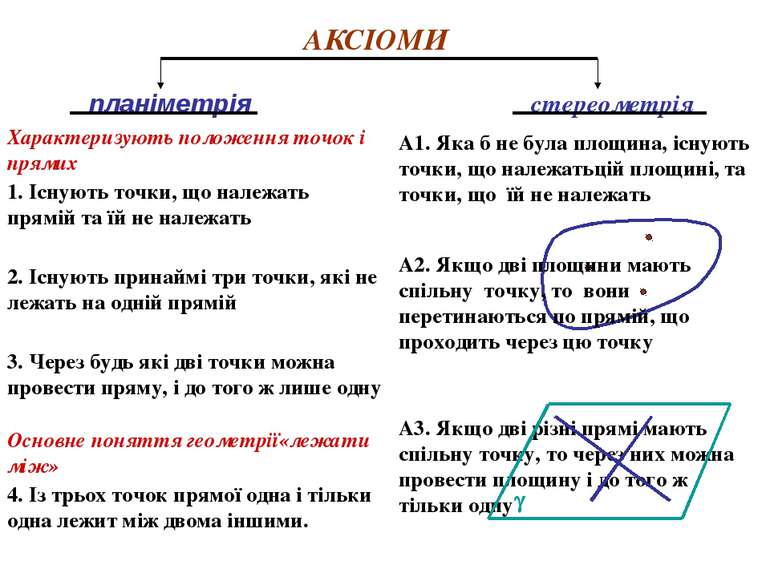
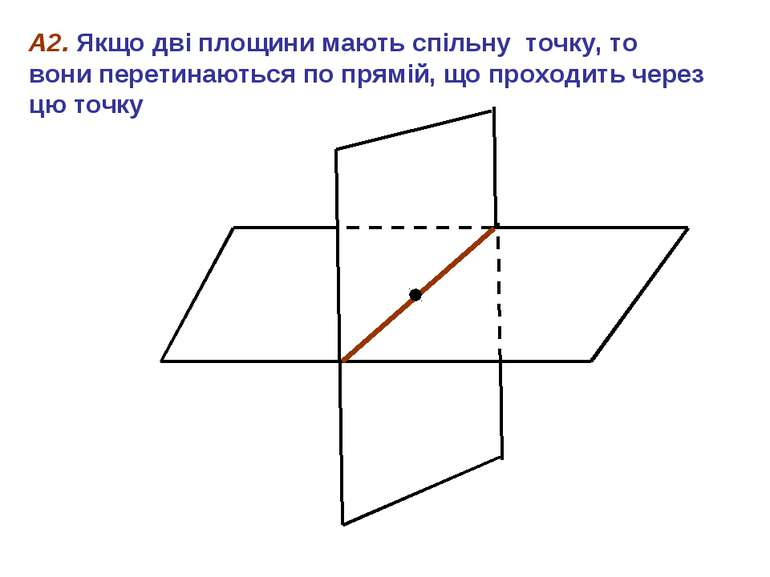
АКСІОМИ планіметрія стереометрія 1. Існують точки, що належать прямій та їй не належать 2. Існують принаймі три точки, які не лежать на одній прямій 3. Через будь які дві точки можна провести пряму, і до того ж лише одну Характеризують положення точок і прямих Основне поняття геометрії«лежати між» 4. Із трьох точок прямої одна і тільки одна лежит між двома іншими. А1. Яка б не була площина, існують точки, що належатьцій площині, та точки, що їй не належать А3. Якщо дві різні прямі мають спільну точку, то через них можна провести площину і до того ж тільки одну А2. Якщо дві площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку

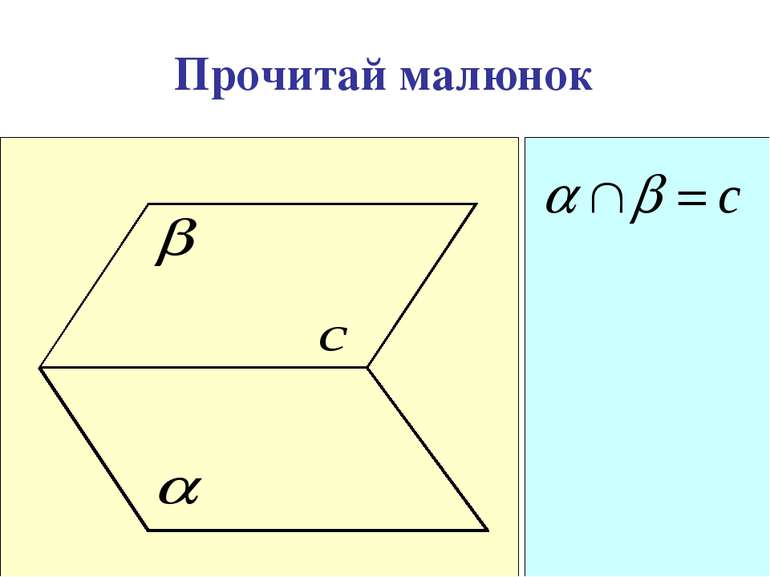
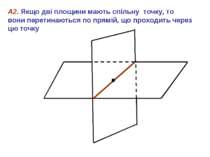
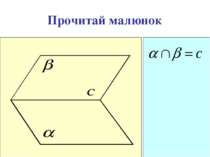
А2. Якщо дві площини мають спільну точку, то вони перетинаються по прямій, що проходить через цю точку

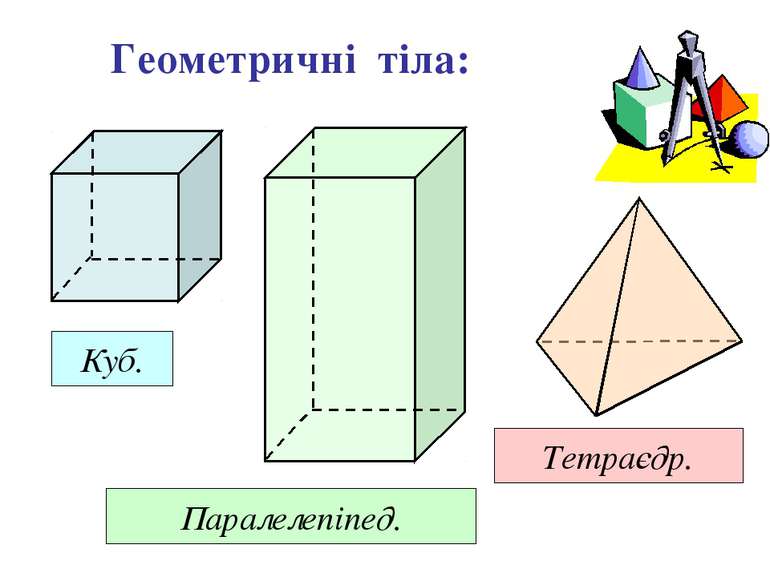
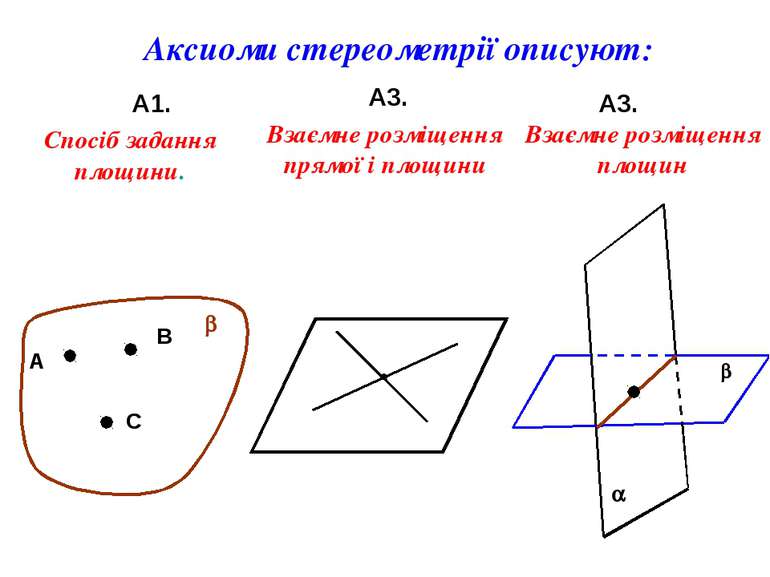
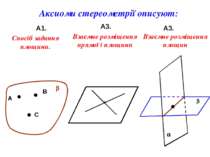
Аксиоми стереометрії описуют: А1. А3. А3. А В С b Спосіб задання площини. Взаємне розміщення прямої і площини a b Взаємне розміщення площин

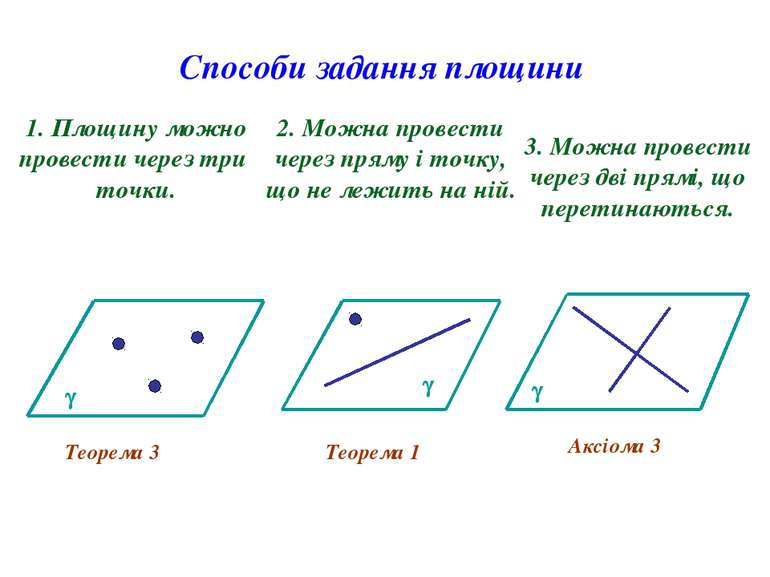
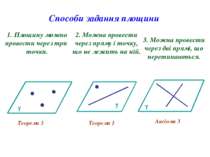
Способи задання площини 1. Площину можно провести через три точки. 2. Можна провести через пряму і точку, що не лежить на ній. Теорема 3 Теорема 1 Аксіома 3 3. Можна провести через дві прямі, що перетинаються.

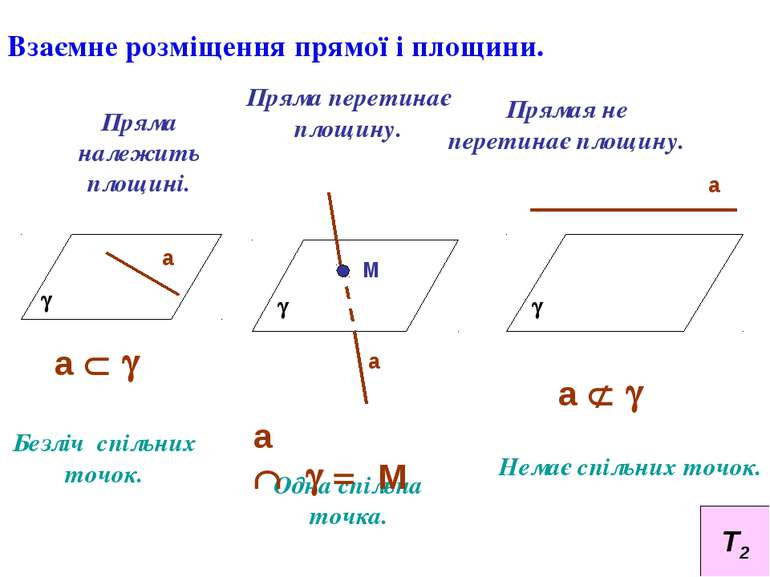
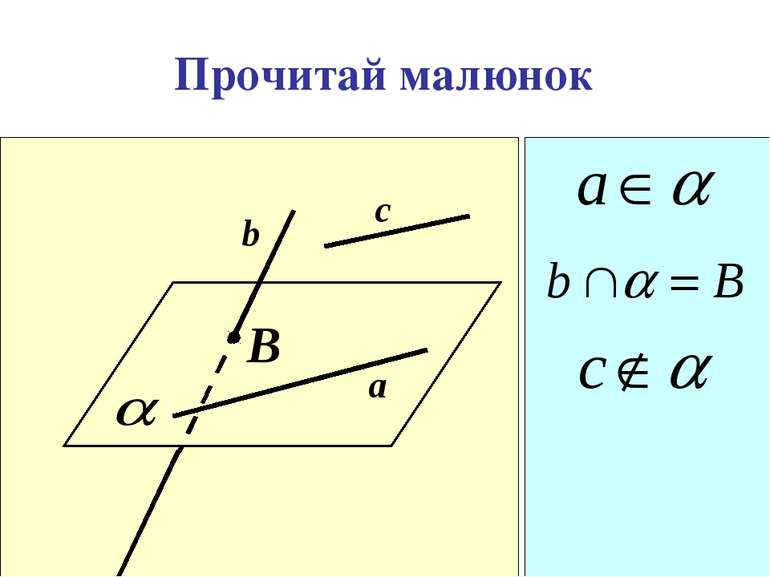
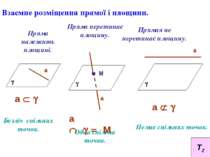
Взаємне розміщення прямої і площини. Пряма належить площині. Пряма перетинає площину. Прямая не перетинає площину. Безліч спільних точок. Одна спільна точка. Немає спільних точок. g а g а М g а а Ì g а Ç g = М а Ë g Т2

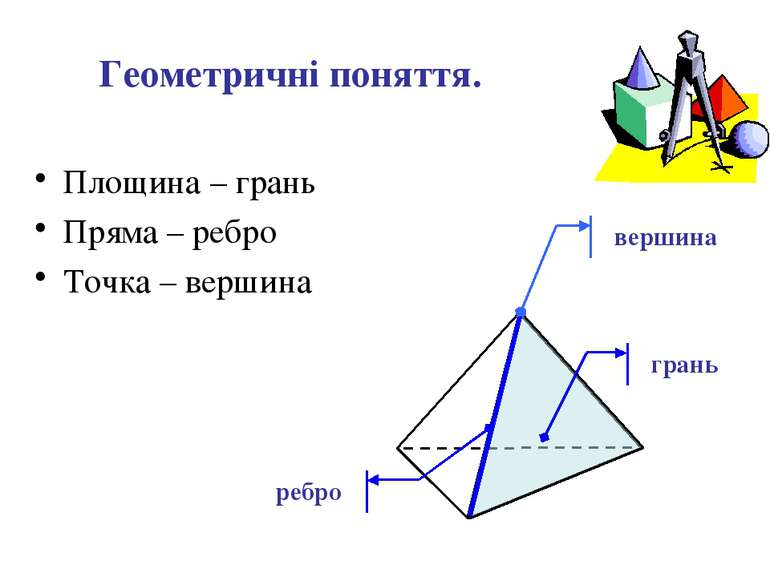
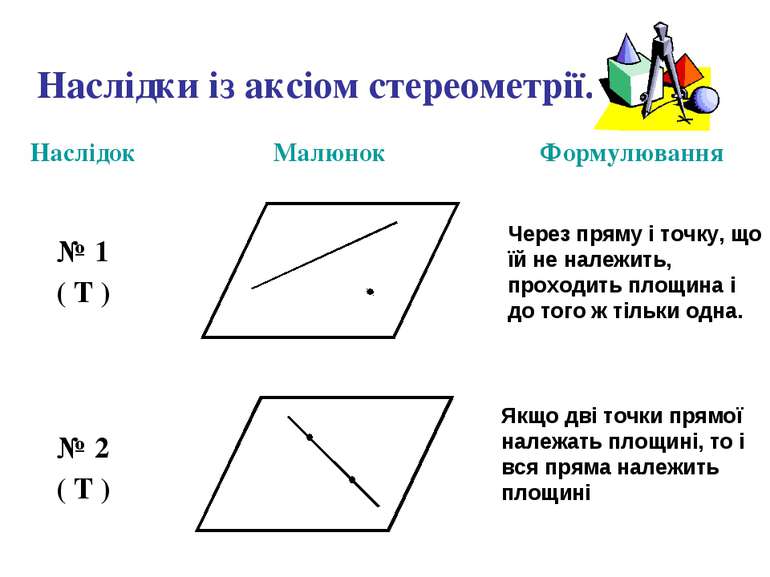
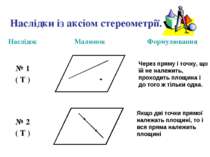
Наслідки із аксіом стереометрії. Через пряму і точку, що їй не належить, проходить площина і до того ж тільки одна. Якщо дві точки прямої належать площині, то і вся пряма належить площині

Наслідки із аксіом стереометрії. Через три точки, що не лежать на одній прямій, можна провести площину і до того ж тільки одну.

Прочитай малюнок A С

Прочитай малюнок B c b a

Прочитай малюнок

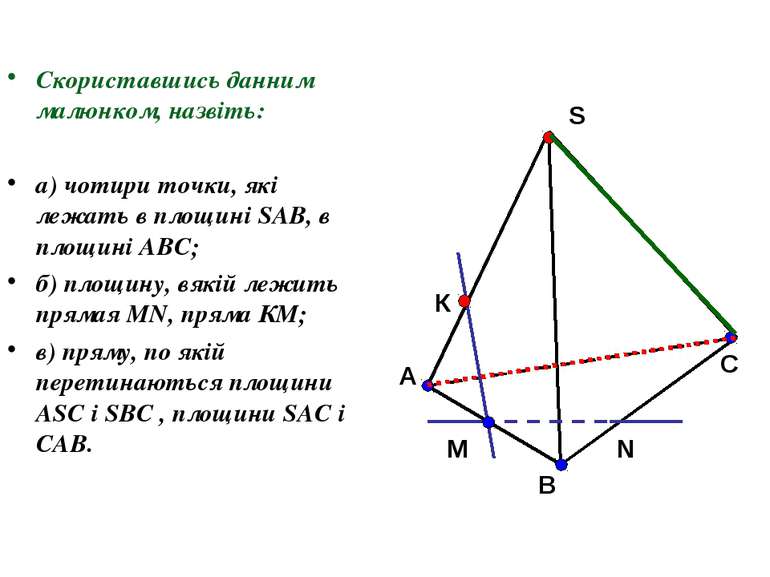
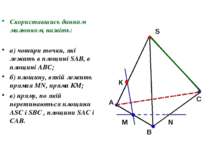
Скориставшись данним малюнком, назвіть: а) чотири точки, які лежать в площині SAB, в площині АВС; б) площину, вякій лежить прямая MN, пряма КМ; в) пряму, по якій перетинаються площини ASC і SBC , площини SAC і CAB.

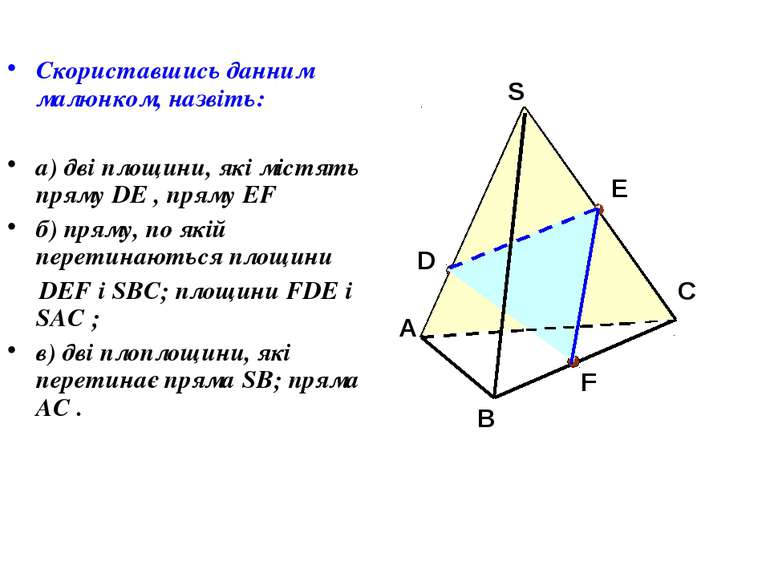
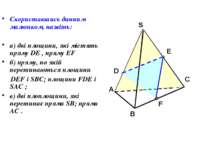
Скориставшись данним малюнком, назвіть: а) дві площини, які містять пряму DE , пряму EF б) пряму, по якій перетинаються площини DEF і SBC; площини FDE і SAC ; в) дві плоплощини, які перетинає пряма SB; пряма AC .

Скориставшись данним малюнком, назвіть: а) три площини, які містять пряму В1С; пряму АВ1;

А А1 В В1 С D1 D C1 а) В1С ?

А А1 В В1 С D1 D C1 а) В1С ?

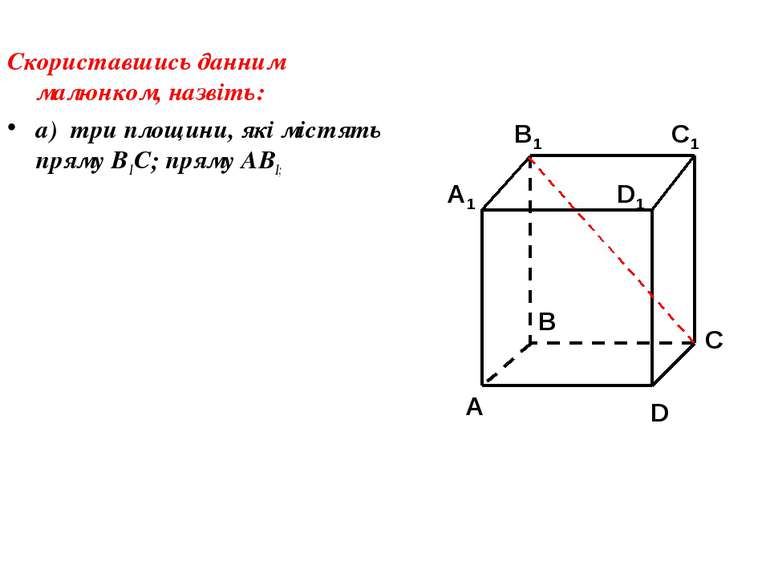
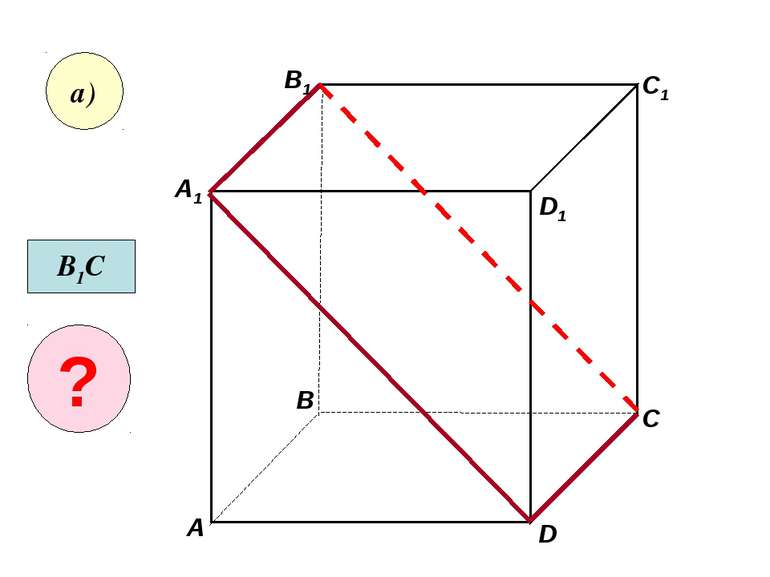
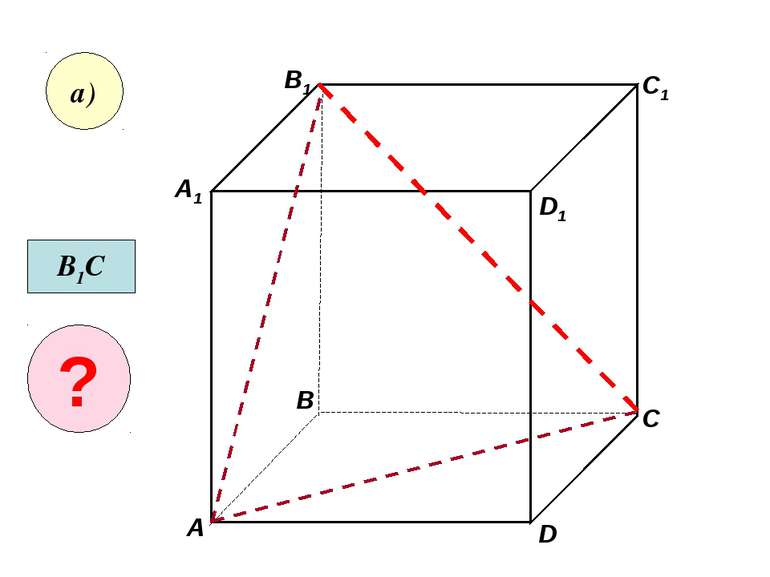
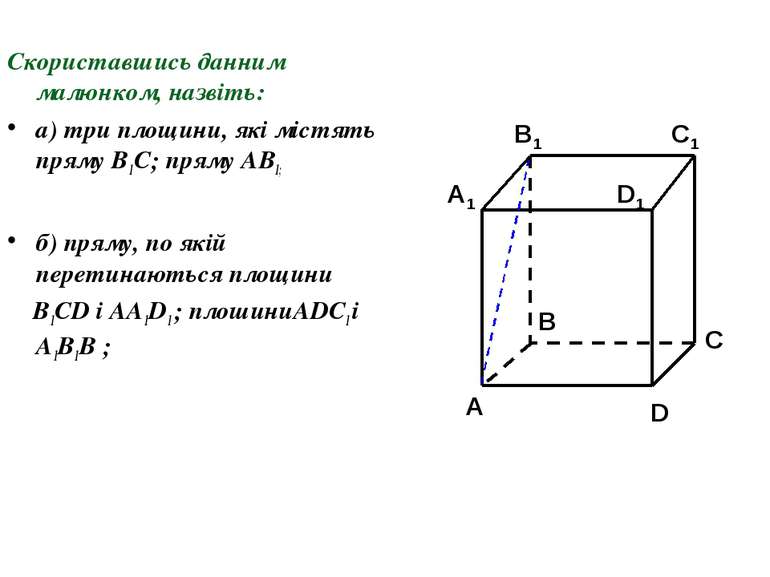
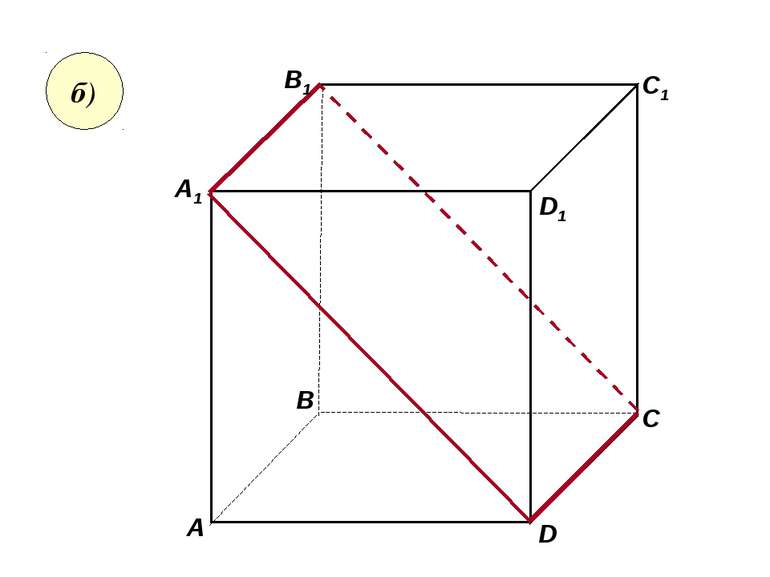
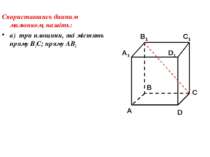
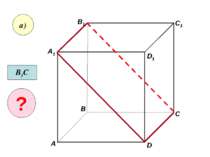
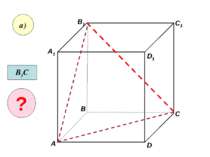
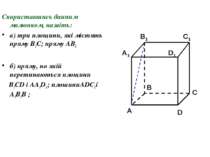
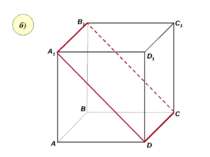
Скориставшись данним малюнком, назвіть: а) три площини, які містять пряму В1С; пряму АВ1; б) пряму, по якій перетинаються площини B1CD і AA1D1 ; плошиниADC1 і A1B1B ; C1 C

А А1 В В1 С D1 D C1 б)

Успіхів