Презентація на тему:
Розв’язування задач з планіметрії

Геометрія 10 клас За підручником М.І. Бурда, Н.А. Тарасенкова

Тема: МЕТОДИ РОЗВ’ЯЗУВАННЯ ПЛАНІМЕТРИЧНИХ ЗАДАЧ

Розв’язування геометричної задачі Слід дотримуватися такого плану: 1) відшукайте на малюнку трикутник (або утворіть його, провівши потрібні відрізки), який можна розв’язати; 2) задача буде розв’язаною, якщо знайдений елемент трикутника задовольняє умову задачі; 3) якщо ні, то, враховуючи знайдений елемент, відшукайте на малюнку другий трикутник. Якщо задачу задовольняє знайдений елемент другого трикутника, – вона розв’язана. В іншому випадку розгляньте третій трикутник і т. д. доти, поки не дістанете такий трикутник, сторона чи кут якого дає розв’язок задачі.

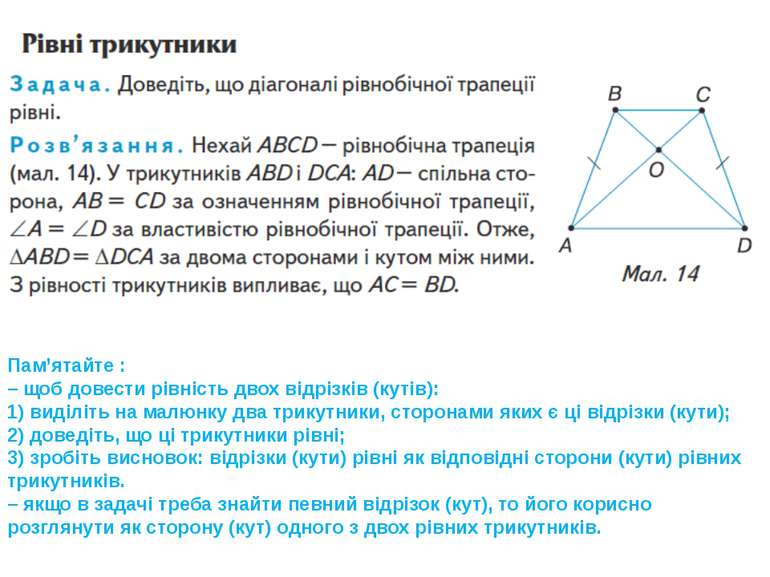
Пам’ятайте : – щоб довести рівність двох відрізків (кутів): 1) виділіть на малюнку два трикутники, сторонами яких є ці відрізки (кути); 2) доведіть, що ці трикутники рівні; 3) зробіть висновок: відрізки (кути) рівні як відповідні сторони (кути) рівних трикутників. – якщо в задачі треба знайти певний відрізок (кут), то його корисно розглянути як сторону (кут) одного з двох рівних трикутників.

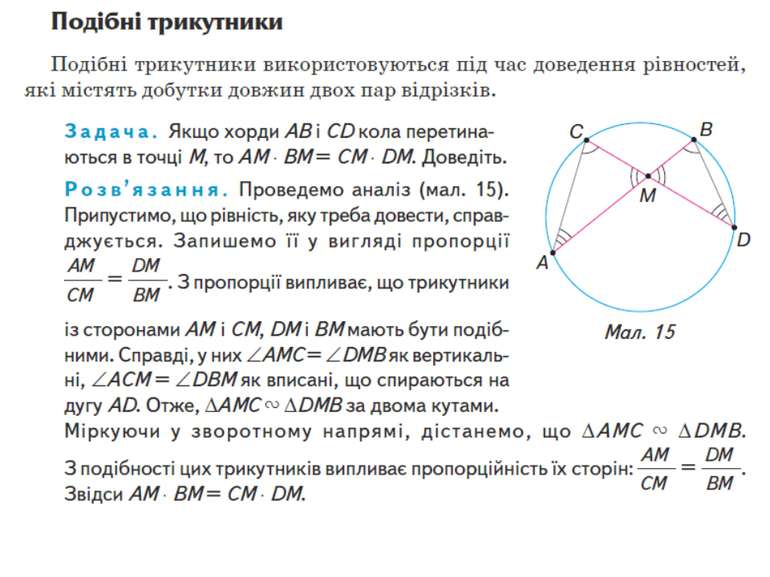
Алгоритм доведення – щоб довести рівність добутків двох пар відрізків: 1) припустіть правильність рівності, яку доводите; 2) запишіть її у вигляді пропорції; 3) відшукайте на малюнку (або побудуйте) трикутники, довжини сторін яких є членами утвореної пропорції; 4) обґрунтуйте подібність цих трикутників. – якщо в задачі треба знайти певний відрізок, то його корисно розглянути як сторону одного з двох подібних трикутників і скласти відповідну пропорцію.

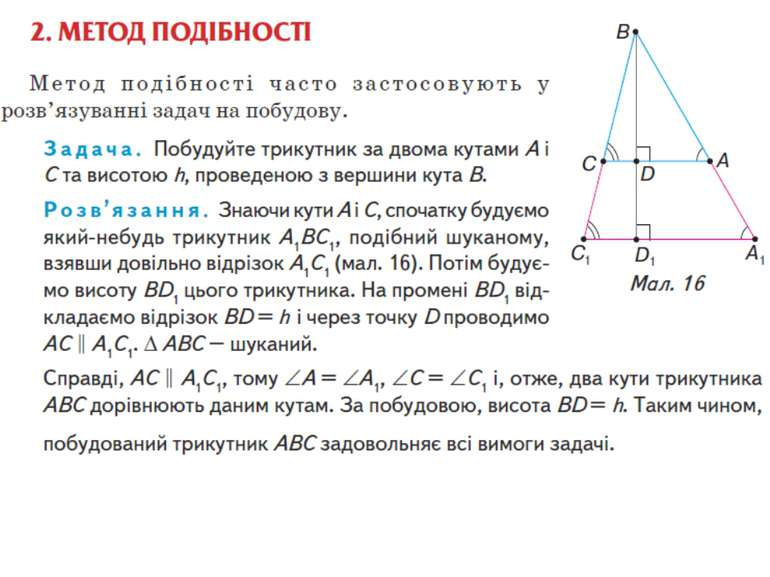
Метод подібності розв’язуючи задачі на побудову методом подібності: 1) виділіть з умови задачі ті дані, які визначають форму шуканого трикутника (відношення відрізків і кути); 2) побудуйте за цими даними допоміжний трикутник, подібний шуканому; 3) побудуйте шуканий трикутник, використавши ті дані умови, які визначають його розміри (довжини відрізків).

Метод геометричних місць Розв’язуючи задачі методом геометричних місць: 1) проаналізуйте умову задачі та виділіть шукану точку; 2) з’ясуйте, які дві вимоги вона задовольняє; 3) знайдіть геометричне місце точок, що задовольняють: першу вимогу; другу вимогу; 4) зробіть висновок: шукана точка – точка перетину знайдених геометричних місць.

Координатний метод Розв’язуючи задачу координатним методом, виконайте три кроки: 1) запишіть геометричну задачу мовою координат; 2) перетворіть алгебраїчний вираз; 3) перекладіть знайдений результат мовою геометрії.

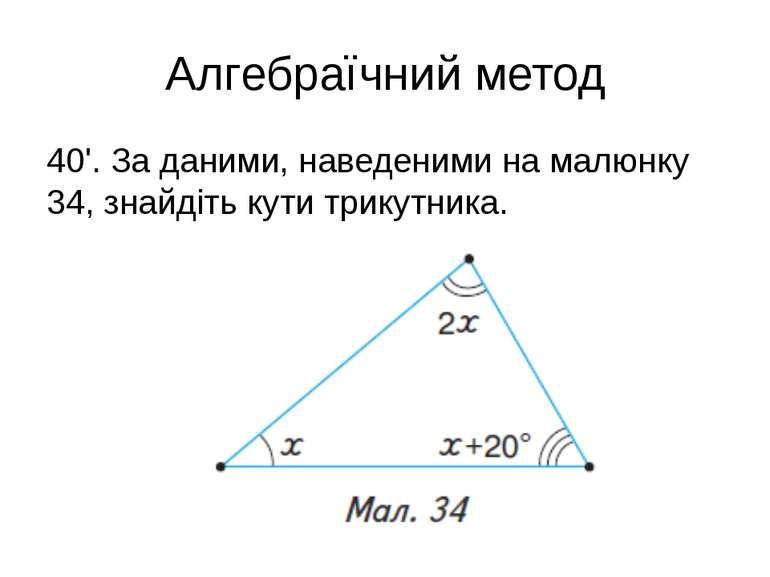
Алгебраїчний метод Розв’язуючи задачі алгебраїчним методом, дотримуйтесь таких етапів: 1) введіть позначення (буквами x, y, z … найчастіше позначаємо шукані величини); 2) складіть рівняння або систему рівнянь, використовуючи відомі геометричні співвідношення між шуканими і даними величинами; 3) розв’яжіть складене рівняння або систему рівнянь. якщо є потреба, то дослідіть знайдені розв’язки.

Метод векторів Щоб застосувати вектори до розв’язування задачі, виконайте три кроки: 1) сформулюйте задачу мовою векторів. Для цього спочатку розгляньте деякі дані у задачі відрізки як вектори. Потім складіть векторну рівність; 2) перетворіть векторну рівність, користуючись законами дій над векторами і відомими векторними рівностями; 3) перекладіть знайдений результат мовою геометрії.

Первинне закріплення повтореного матеріалу 1. Назвіть основні фігури та основні відношення в планіметрії. 2. Сформулюйте аксіоми планіметрії. 3. Які кути називаються суміжними; вертикальними? які їх властивості? 4. Сформулюйте властивості й ознаки паралельних прямих. 5. Назвіть основні співвідношення між сторонами і кутами довільного трикутника; прямокутного трикутника. 6. За якими формулами можна обчислити площу трикутника? 7. Які є ознаки рівності трикутників? а подібності? 8. Дайте означення паралелограма, прямокутника, ромба, квадрата, трапеції. Які їх властивості? 9. Який многокутник називається вписаним у коло? Описаним навколо кола? 10. Які властивості трикутника, вписаного у коло, і трикутника, описаного навколо кола? а чотирикутника? 11. Що таке правильний многокутник та які його властивості? 12. Як використовують під час розв’язування задач допоміжні трикутники (один або кілька нерівних трикутників, рівні трикутники, подібні трикутники)? 13. У чому полягає суть методу подібності? методу геометричних місць? 14. Назвіть кроки розв’язування задач методом координат. 15. Поясніть суть етапів алгебраїчного методу розв’язування задач.

Тренувальні вправи

Тренувальні вправи

Знайдіть на малюнках 27 – 29 рівні трикутники. Поясніть, чому вони рівні.

Тренувальні вправи, складання алгоритму їх розв'язання

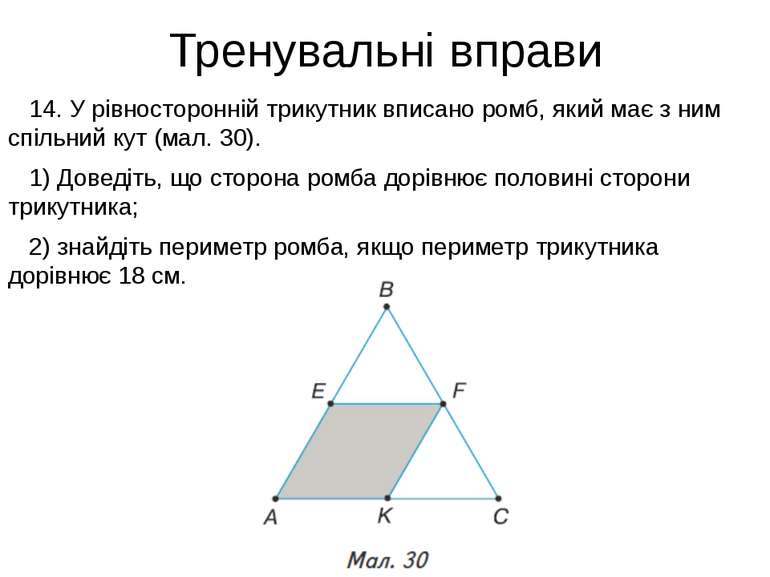
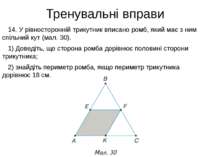
Тренувальні вправи 14. У рівносторонній трикутник вписано ромб, який має з ним спільний кут (мал. 30). 1) Доведіть, що сторона ромба дорівнює половині сторони трикутника; 2) знайдіть периметр ромба, якщо периметр трикутника дорівнює 18 см.

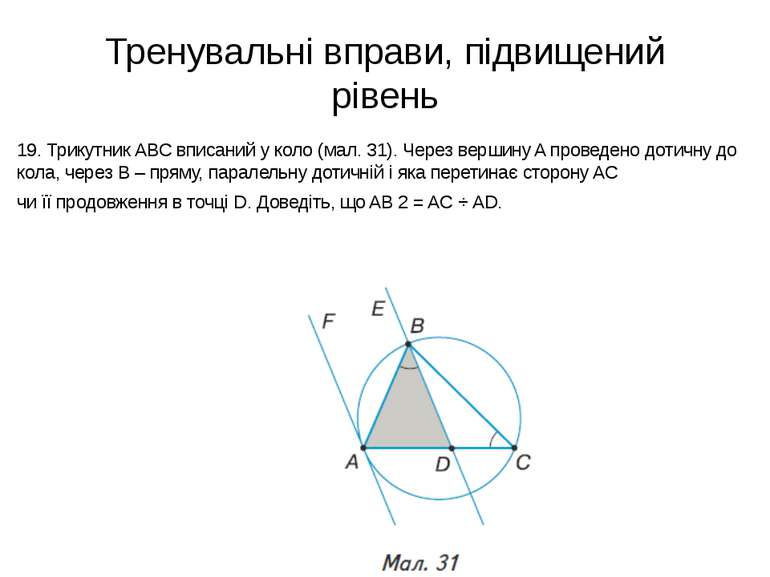
Тренувальні вправи, підвищений рівень 19. Трикутник ABC вписаний у коло (мал. 31). Через вершину A проведено дотичну до кола, через B – пряму, паралельну дотичній і яка перетинає сторону AC чи її продовження в точці D. Доведіть, що AB 2 = AC ⋅ AD.

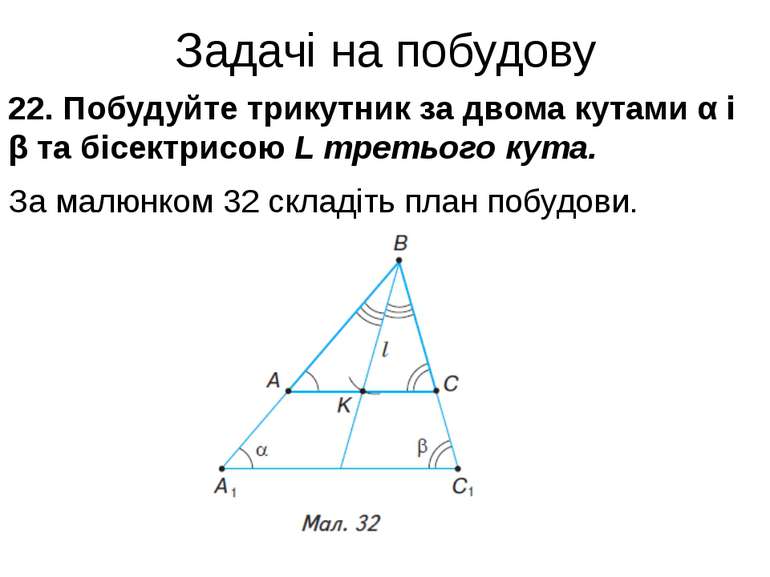
Задачі на побудову 22. Побудуйте трикутник за двома кутами α і β та бісектрисою L третього кута. За малюнком 32 складіть план побудови.

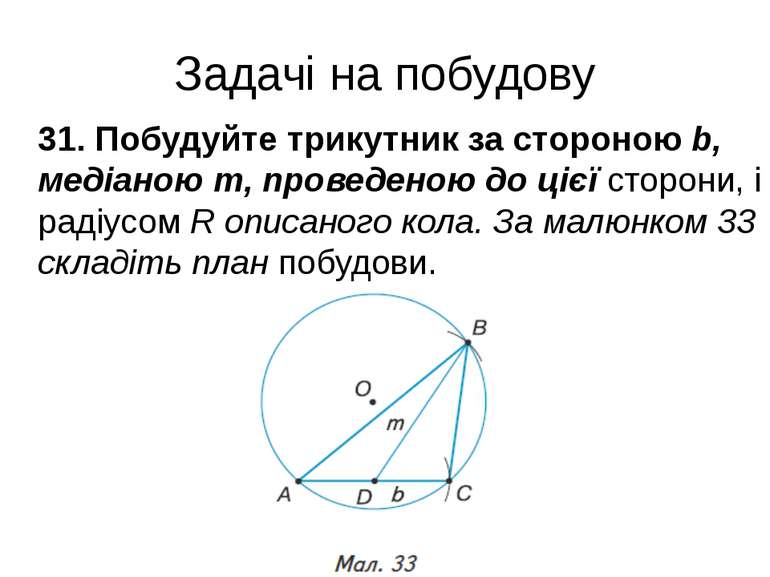
Задачі на побудову 31. Побудуйте трикутник за стороною b, медіаною m, проведеною до цієї сторони, і радіусом R описаного кола. За малюнком 33 складіть план побудови.

Алгебраїчний метод 40'. За даними, наведеними на малюнку 34, знайдіть кути трикутника.

Тестова перевірка знань (15 хв.)