Презентація на тему:
Перпендикуляр і похила до площини, відстані та кути у просторі

Перпендикуляр і похила

Епіграф Геометрія, учителька точності, готує наш розум до глибинних досліджень природи. Т.Ф. Осиповський Головне значення перпендикуляра – це його роль у техніці і у всьому нашому вжитку. О.Д. Александров

Мета уроку сформувати поняття перпендикуляра до площини; похилої; проекції похилої на площину; відстань від точки до площини; установити взаємозв’язок між довжинами похилих, проведених з однієї точки до площини, і довжинами їхніх проекцій на площину. розвивати вміння застосовувати здобуті знання для розв’язування задач.

1. Сформулюйте означення перпендикулярних прямих. 2. Дайте означення прямої, перпендикулярної до площини. 3. Сформулюйте ознаку перпендикулярності прямої та площини. 5. Скільки прямих, перпендикулярних до даної площини, можна провести через дану точку? Бліц-опитування

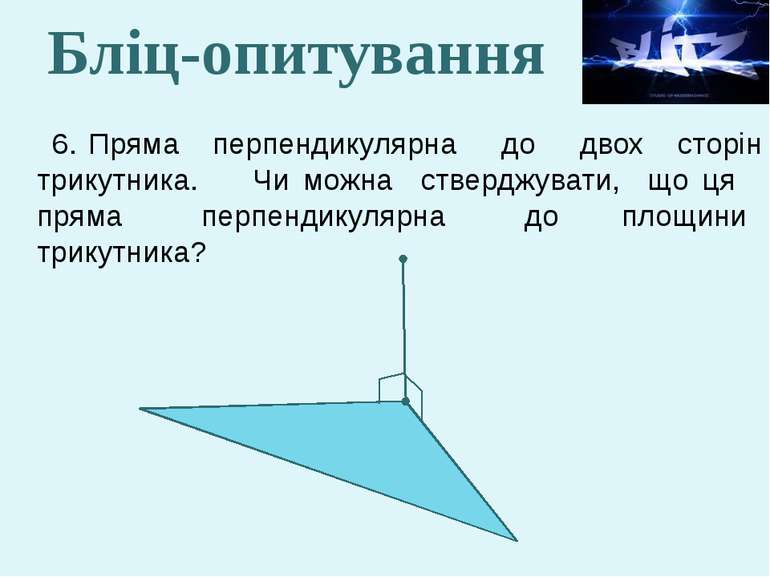
6. Пряма перпендикулярна до двох сторін трикутника. Чи можна стверджувати, що ця пряма перпендикулярна до площини трикутника? Бліц-опитування

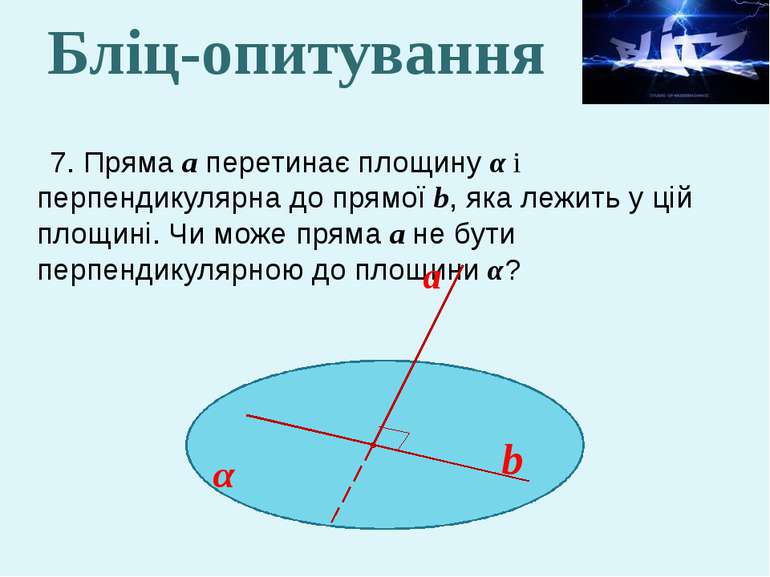
7. Пряма а перетинає площину α і перпендикулярна до прямої b, яка лежить у цій площині. Чи може пряма а не бути перпендикулярною до площини α? а α b Бліц-опитування

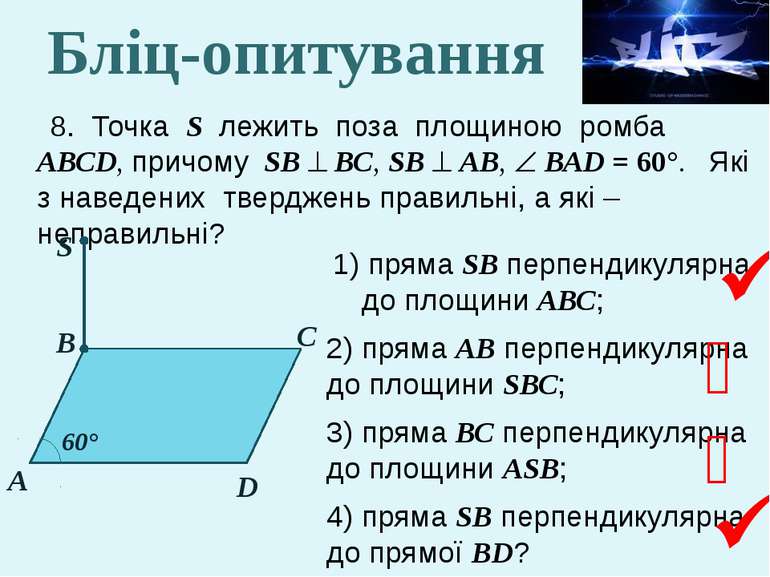
8. Точка S лежить поза площиною ромба АВСD, причому SВ ВС, SВ АВ, ВАD = 60°. Які з наведених тверджень правильні, а які – неправильні? 1) пряма SВ перпендикулярна до площини АВС; 2) пряма АВ перпендикулярна до площини SВС; 3) пряма ВС перпендикулярна до площини АSВ; 4) пряма SВ перпендикулярна до прямої ВD? S 60° В А D С Бліц-опитування

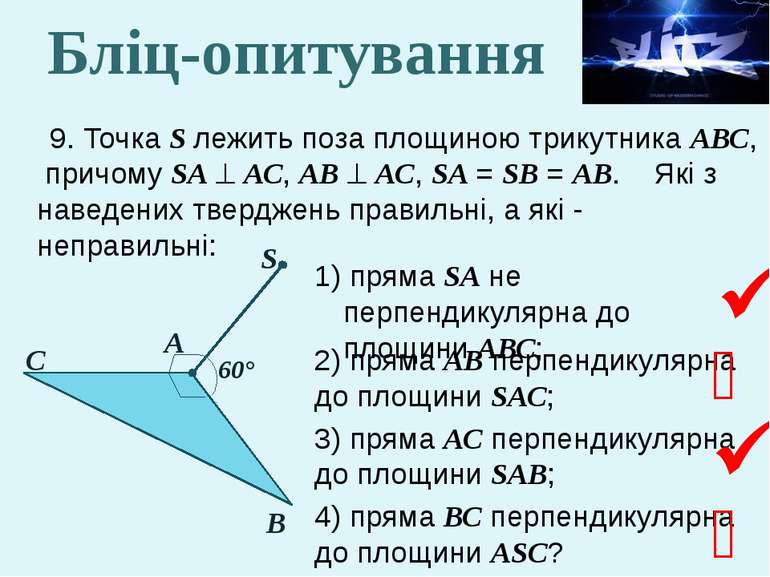
9. Точка S лежить поза площиною трикутника АВС, причому SА АС, АВ АС, SА = SВ = АВ. Які з наведених тверджень правильні, а які - неправильні: 1) пряма SА не перпендикулярна до площини АВС; 2) пряма АВ перпендикулярна до площини SАС; 3) пряма АС перпендикулярна до площини SАВ; 4) пряма ВС перпендикулярна до площини АSС? S В А С 60° Бліц-опитування

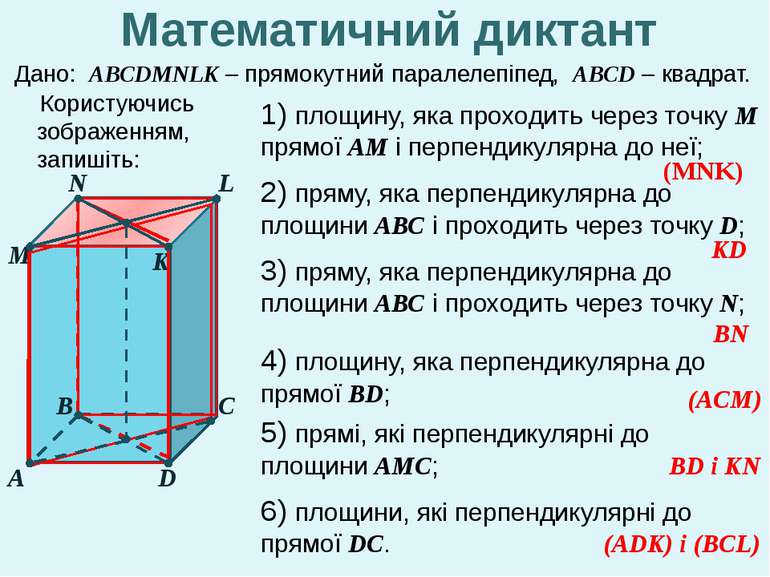
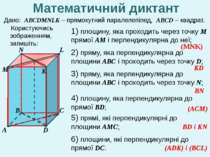
Математичний диктант 1) площину, яка проходить через точку М прямої АМ і перпендикулярна до неї; Користуючись зображенням, запишіть: 2) пряму, яка перпендикулярна до площини АВС і проходить через точку D; 3) пряму, яка перпендикулярна до площини АВС і проходить через точку N; 4) площину, яка перпендикулярна до прямої ВD; 5) прямі, які перпендикулярні до площини АМС; 6) площини, які перпендикулярні до прямої DС. А В М D С L N K (MNK) KD BN (ACM) BD і KN (ADK) і (BCL) Дано: АВСDMNLK – прямокутний паралелепіпед, АВСD – квадрат.

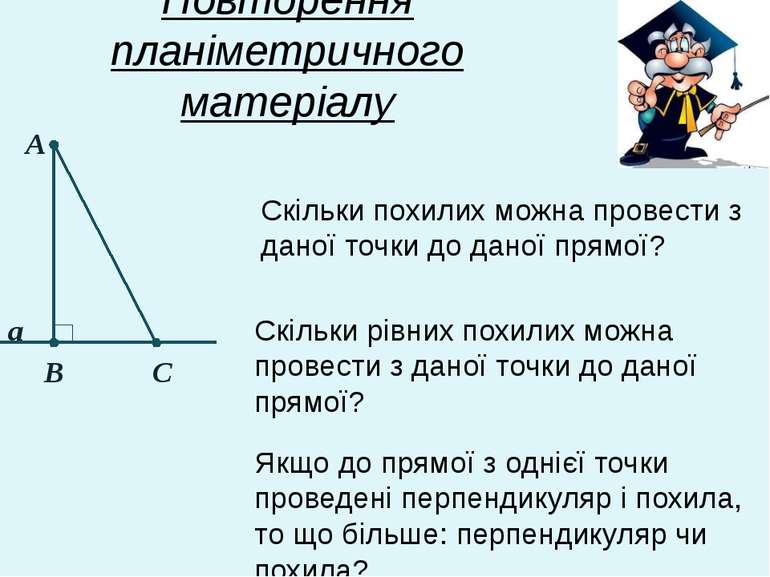
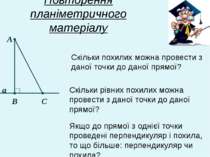
Повторення планіметричного матеріалу Як називають відрізок АВ? А В С а Як називають відрізок АC? Як називають точку В, точку С? Як називають відрізок ВC? Скільки перпендикулярів можна провести з даної точки до даної прямої?

Повторення планіметричного матеріалу Скільки рівних похилих можна провести з даної точки до даної прямої? А В С а Якщо до прямої з однієї точки проведені перпендикуляр і похила, то що більше: перпендикуляр чи похила? Скільки похилих можна провести з даної точки до даної прямої?

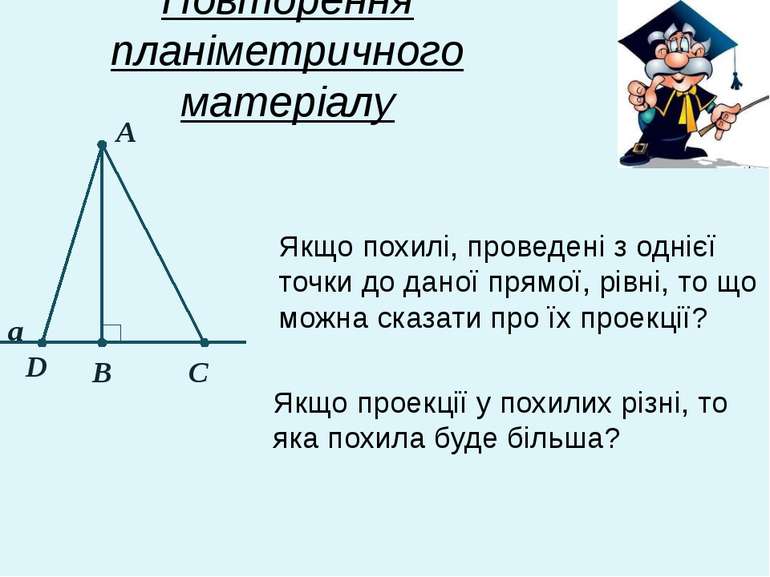
Повторення планіметричного матеріалу Якщо проекції у похилих різні, то яка похила буде більша? А В С а Якщо похилі, проведені з однієї точки до даної прямої, рівні, то що можна сказати про їх проекції? D

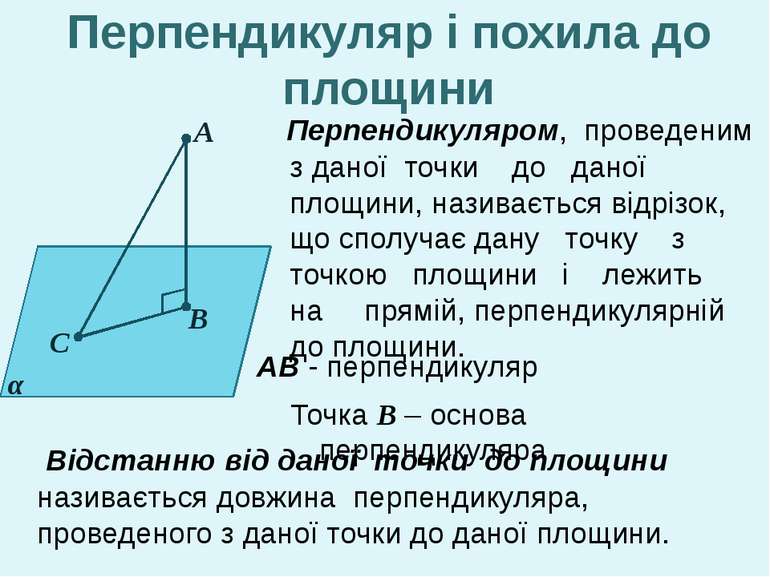
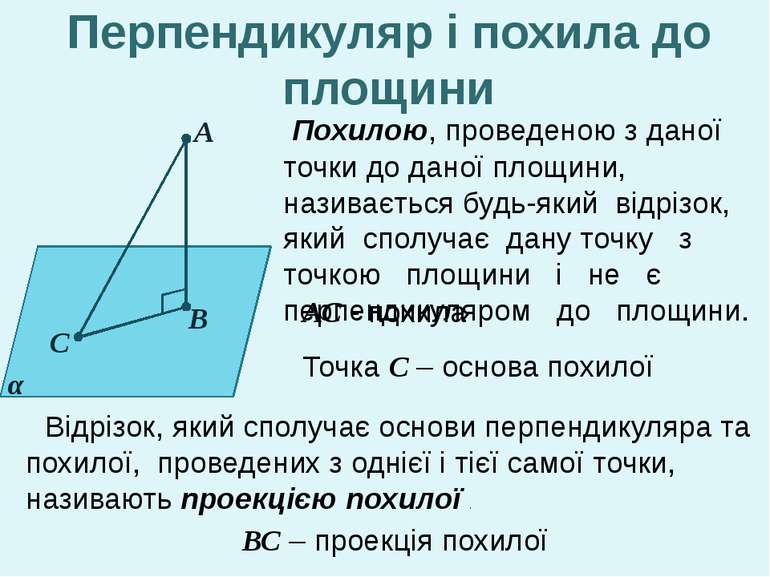
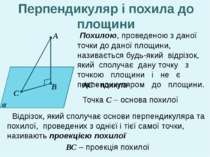
А В С α Перпендикуляром, проведеним з даної точки до даної площини, називається відрізок, що сполучає дану точку з точкою площини і лежить на прямій, перпендикулярній до площини. Точка В – основа перпендикуляра Відстанню від даної точки до площини називається довжина перпендикуляра, проведеного з даної точки до даної площини. Перпендикуляр і похила до площини АВ - перпендикуляр

А В С α Похилою, проведеною з даної точки до даної площини, називається будь-який відрізок, який сполучає дану точку з точкою площини і не є перпендикуляром до площини. АС - похила Точка С – основа похилої ВС – проекція похилої Перпендикуляр і похила до площини Відрізок, який сполучає основи перпендикуляра та похилої, проведених з однієї і тієї самої точки, називають проекцією похилої .

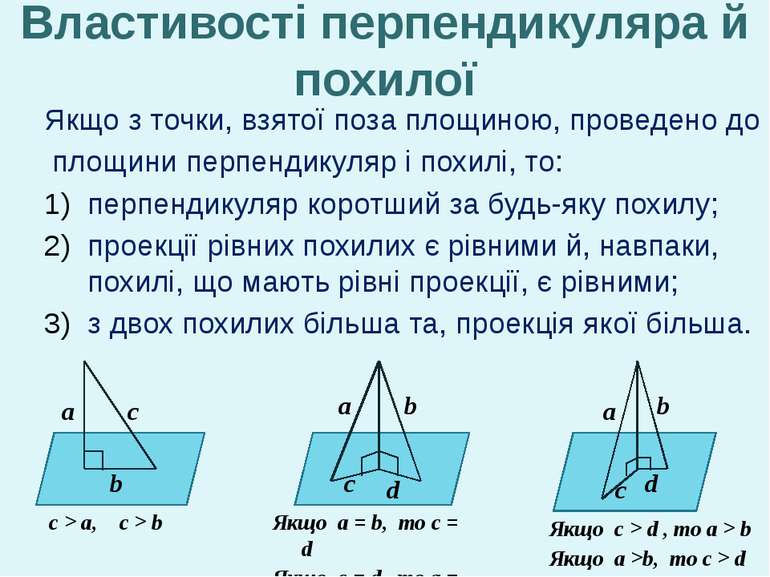
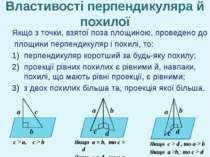
Властивості перпендикуляра й похилої Якщо з точки, взятої поза площиною, проведено до площини перпендикуляр і похилі, то: перпендикуляр коротший за будь-яку похилу; проекції рівних похилих є рівними й, навпаки, похилі, що мають рівні проекції, є рівними; з двох похилих більша та, проекція якої більша. а а а b b b c c c d d c > a, c > b Якщо a = b, то c = d Якщо c = d , то a = b Якщо c > d , то a > b Якщо a >b, то c > d

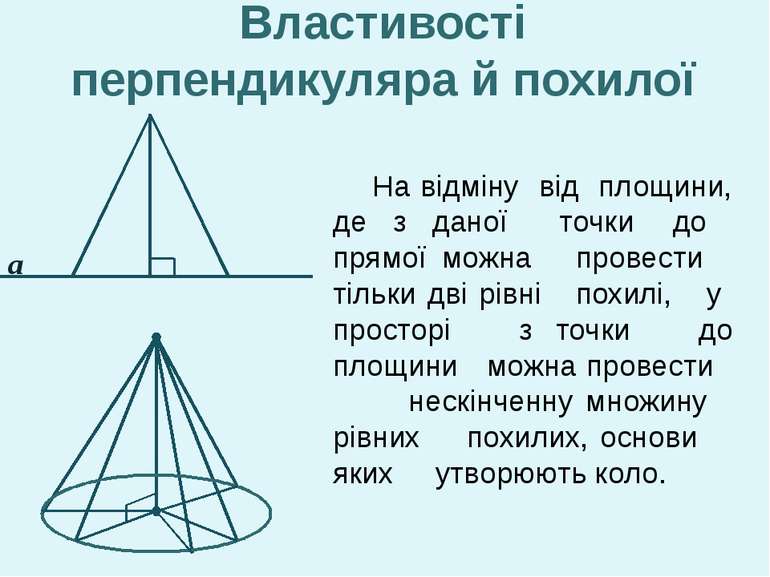
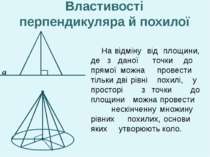
На відміну від площини, де з даної точки до прямої можна провести тільки дві рівні похилі, у просторі з точки до площини можна провести нескінченну множину рівних похилих, основи яких утворюють коло. Властивості перпендикуляра й похилої а

Властивості перпендикуляра і похилої застосовуються на практиці. Наприклад, якщо встановлюють щоглу на радіостанції, то стяжки беруть рівної довжини. Нижні кінці їх закріпляють на однакових відстанях від основи щогли (рівномірно по колу). Це сприяє стійкості щогли. Властивості перпендикуляра й похилої

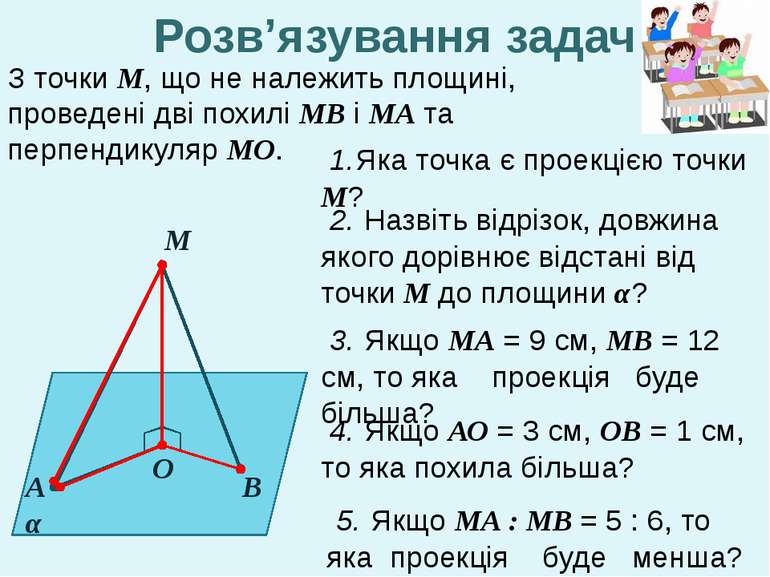
М А α О В 1.Яка точка є проекцією точки М? 2. Назвіть відрізок, довжина якого дорівнює відстані від точки М до площини α? 3. Якщо МА = 9 см, МВ = 12 см, то яка проекція буде більша? 5. Якщо МА : МВ = 5 : 6, то яка проекція буде менша? 4. Якщо АО = 3 см, ОВ = 1 см, то яка похила більша? З точки М, що не належить площині, проведені дві похилі МВ і МА та перпендикуляр МО. Розв’язування задач

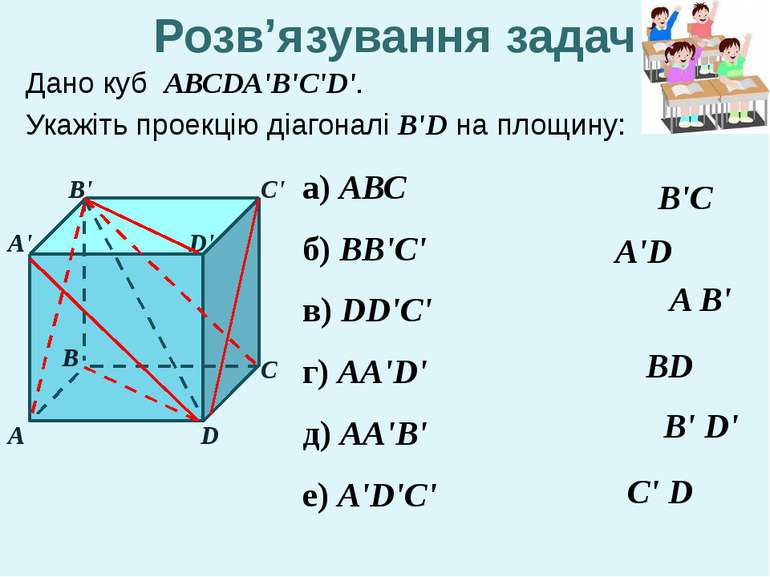
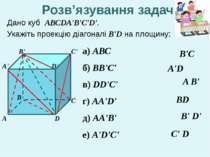
Дано куб АВСDA'B'C'D'. Укажіть проекцію діагоналі B'D на площину: А В С С' D D' В' А' а) АВС б) ВВ'С' в) DD'C' г) AA'D' д) AA'B' е) A'D'C' ВD В'C C' D A'D A В' В' D' Розв’язування задач

Розв’язування задач Розв’язання простіших задач на похилу та її проекцію на площину зводиться до розв’язання прямокутного трикутника, сторонами якого є похила, її проекція на площину і перпендикуляр до площини. Якщо такого трикутника немає на малюнку, то, щоб його утворити, проводимо допоміжні відрізки.

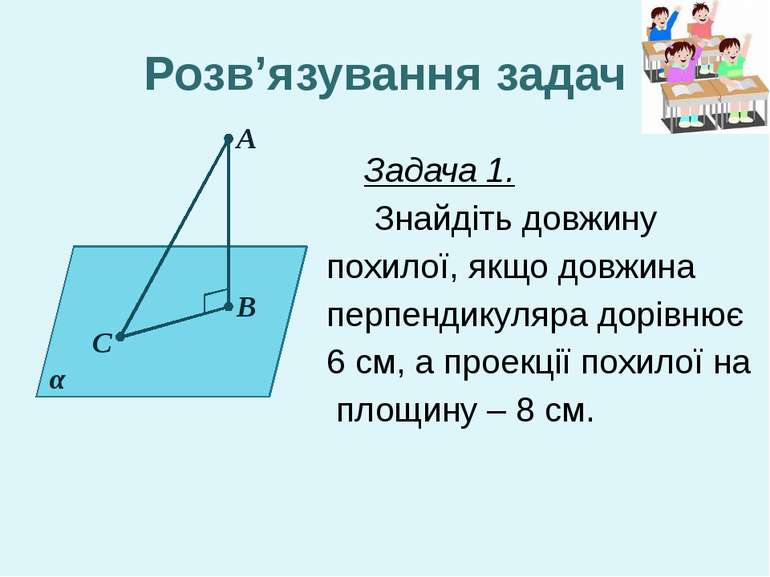
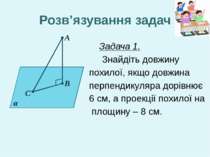
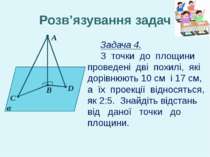
Задача 1. Знайдіть довжину похилої, якщо довжина перпендикуляра дорівнює 6 см, а проекції похилої на площину – 8 см. А В С α Розв’язування задач

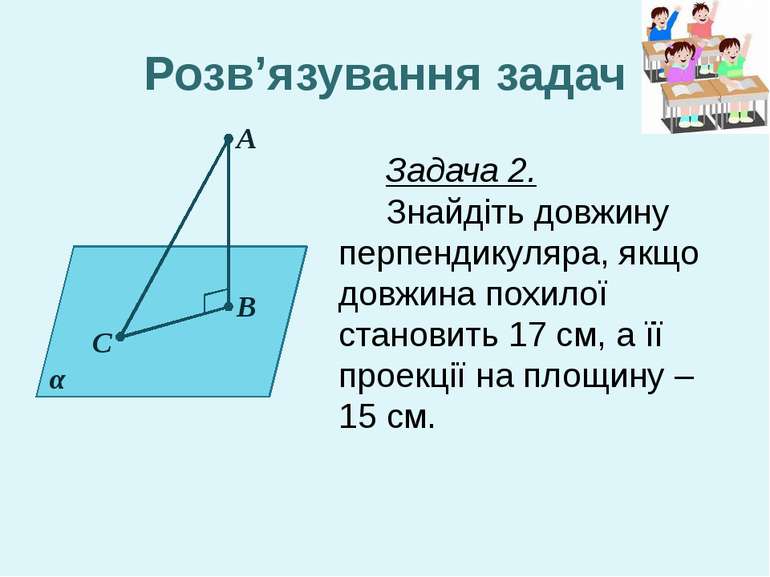
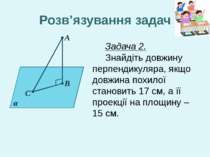
А В С α Розв’язування задач Задача 2. Знайдіть довжину перпендикуляра, якщо довжина похилої становить 17 см, а її проекції на площину – 15 см.

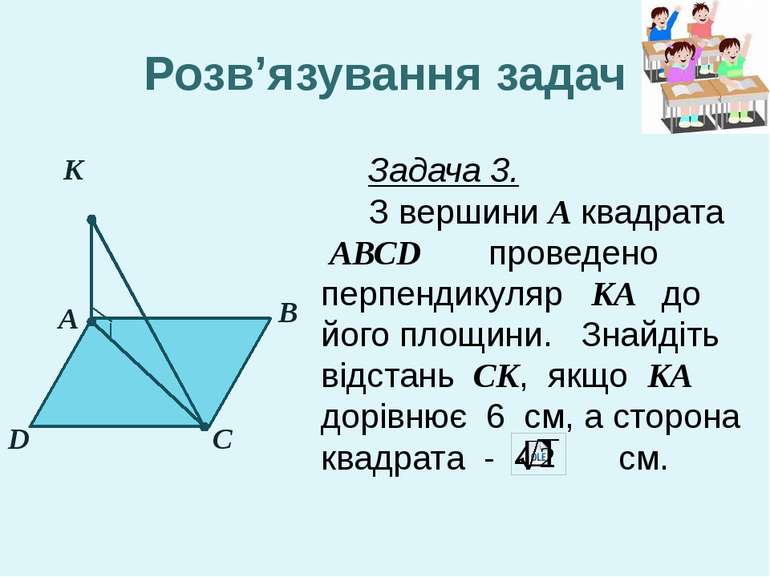
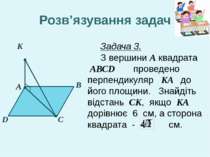
A D B C K Розв’язування задач Задача 3. З вершини A квадрата АВСD проведено перпендикуляр KA до його площини. Знайдіть відстань CK, якщо KA дорівнює 6 см, а сторона квадрата - 4 см.

Розв’язування задач Якщо в задачі йдеться про дві похилі, проведені з однієї точки до площини, то розглядаємо два прямокутних трикутники, спільним катетом яких є перпендикуляр, опущений з даної точки на площину. А В С О З ∆АОВ та ∆АОС: АО2 = АВ2 – ОВ2 = АС2 – ОС2

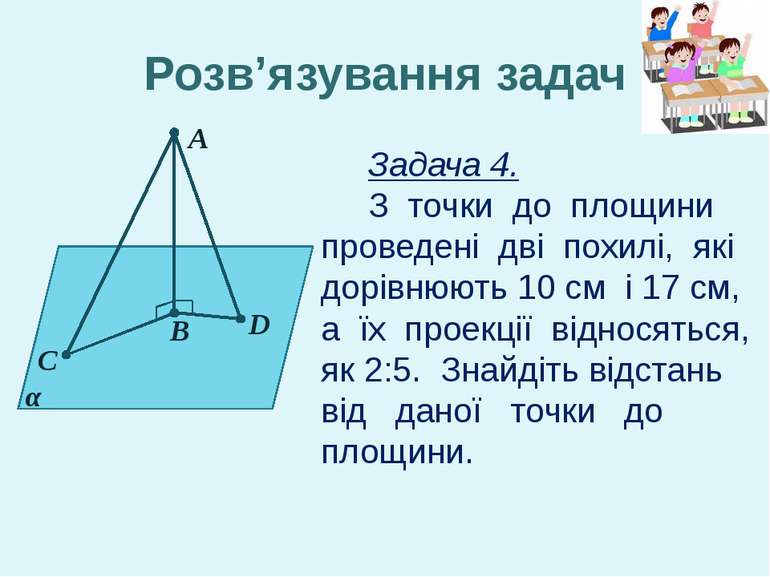
А C α B D Розв’язування задач Задача 4. З точки до площини проведені дві похилі, які дорівнюють 10 см і 17 см, а їх проекції відносяться, як 2:5. Знайдіть відстань від даної точки до площини.

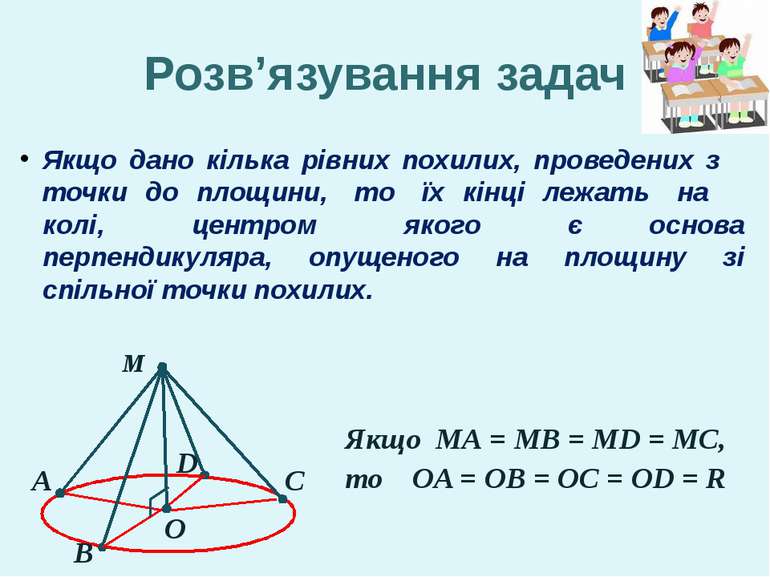
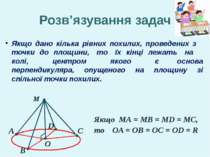
Розв’язування задач Якщо дано кілька рівних похилих, проведених з точки до площини, то їх кінці лежать на колі, центром якого є основа перпендикуляра, опущеного на площину зі спільної точки похилих. М А В С D О Якщо МА = МВ = MD = MC, то OA = OB = OC = OD = R

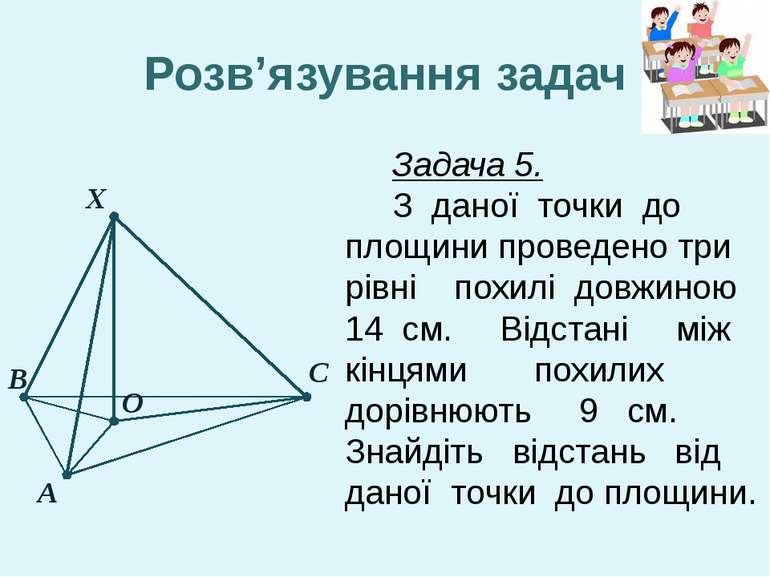
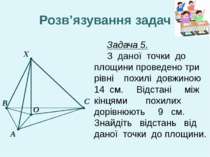
X А В С О Розв’язування задач Задача 5. З даної точки до площини проведено три рівні похилі довжиною 14 см. Відстані між кінцями похилих дорівнюють 9 см. Знайдіть відстань від даної точки до площини.

1. Найкоротша відстань від точки до площини. К р о с в о р д 2. Похилі, які мають рівні проекції, ………. . 3. Трикутник це геометрична ………. . 4. Кінець перпендикуляра, що лежить у площині. 5. Одна із сторін прямокутного трикутника. 7. Відрізок, що сполучає основи перпендикуляра і похилої, проведених з однієї точки. 6. Відрізок, який сполучає дану точку, з точкою площини, але не перпендикуляр. Ключове слово: П І Ф А Г О Р

Вивчити § 38, розв'язати задачі №223, №241, ст. 209. Домашнє завдання

Дякуємо за урок!