Презентація на тему:
Підмножина. Операції над множинами

Алгебра і початки аналізу. 10 клас (за підручником Мерзляк А. Г.)

Тема уроку: Підмножина. Операції над множинами

Підмножина. Операції над множинами Розглянемо множину цифр десяткової системи числення A = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. Виокремимо з множини A ті її елементи, які є парними цифрами. Отримаємо множину B = {0, 2, 4, 6, 8}, усі елементи якої є елементами множини A. Означення. Множину B називають підмножиною множини A, якщо кожний елемент множини B є елементом множини A. Це записують так: B ⊂ A або A ⊃ B (читають: «множина B є підмножиною множини A» або «множина A містить множину B»). Наприклад, N ⊂ Z, Z ⊂ Q, Q ⊃ N, Q ⊂ R, {a} ⊂ {a, b}, (1; 2] ⊂ [1; 2], [2; 5] ⊂ (1; +∞). Множина учнів нашого класу є підмножиною множини учнів нашої школи. Множина ссавців є підмножиною множини хребетних.

Підмножина. Операції над множинами Множина точок променя CB є підмножиною множини точок прямої AB (рис. 1). Для ілюстрації співвідношень між множинами використовують схеми, які називають діаграмами Ейлера. На рисунку 2 зображено множину A (більший круг) і множину B (менший круг, який міститься в більшому). Ця схема означає, що B ⊂ A (або A ⊃ B). На рисунку 3 за допомогою діаграм Ейлера показано співвідношення між множинами N, Z, Q і R. З означень підмножини і рівності множин випливає, що коли A ⊂ B і B ⊂ A, то A = B. Будь-яка множина A є підмножиною самої себе, тобто A ⊂ A.

Якщо в множині B немає такого елемента, який не належить множині A, то множина B є підмножиною множини A. У силу цих міркувань порожню множину вважають підмножиною будь- якої множини. Справді, порожня множина не містить жодного елемента, отже, у ній немає елемента, який не належить даній множині A. Тому для будь-якої множини A справедливе твердження: ∅ ⊂ A. ∅ ⊂ A

Приклад Випишіть усі підмножини множини A = {a, b, c}. Розв’язання. Маємо: {a}, {b}, {c}, {a, b}, {b, c}, {a, c}, {a, b, c}, ∅. Нехай A — множина розв’язків рівняння x + y = 5, а B — множина розв’язків рівняння x – y = 3. Тоді множина C розв’язків системи рівнянь , складається з усіх елементів, які належать і множині A, і множині B. У такому випадку кажуть, що множина C є перетином множин A і B.

Перетин множин Означення. Перетином множин A і B називають множину, яка складається з усіх елементів, що належать і множині A, і множині B. Перетин множин A і B позначають так: A B. Наприклад, [–1; 3) (2; +∞) = (2; 3) (рис. 4).

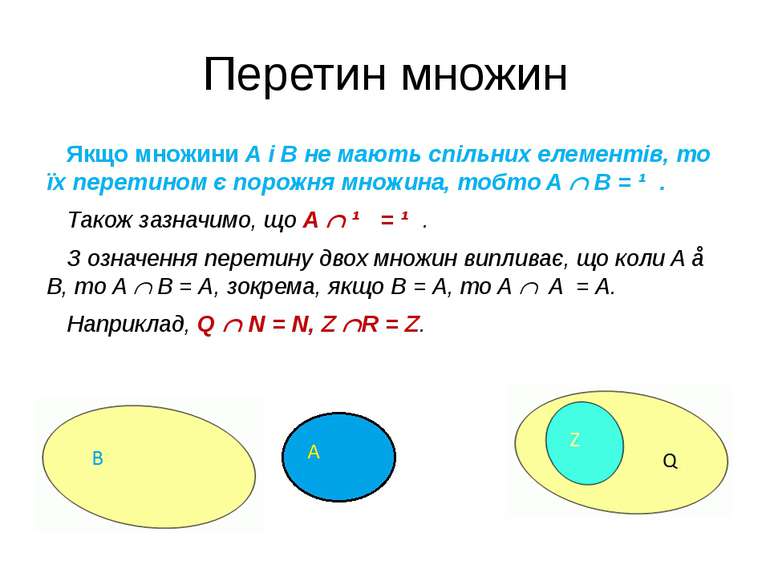
Перетин множин Якщо множини A і B не мають спільних елементів, то їх перетином є порожня множина, тобто A B = ∅. Також зазначимо, що A ∅ = ∅. З означення перетину двох множин випливає, що коли A ⊂ B, то A B = A, зокрема, якщо B = A, то A A = A. Наприклад, Q N = N, Z R = Z.

Перетин множин Перетин множин зручно ілюструвати за допомогою діаграм Ейлера. На рисунку 5 заштрихована фігура зображує множину A B. а) б). Для того щоб розв’язати рівняння , треба розв’язати кожне з рівнянь x2 – x = 0 і x2 – 1 = 0. Маємо: A = {0, 1} — множина коренів першого рівняння, B = {–1, 1} — множина коренів другого рівняння. Зрозуміло, що множина C = {–1, 0, 1}, кожний елемент якої належить або множині A, або множині B, є множиною коренів заданого рівняння. Множину C називають об’єднанням множин A і B.

Об’єднання множин Означення. Об’єднанням множин A і B називають множину, яка складається з усіх елементів, що належать хоча б одній з цих множин: або множині A, або множині B. Об’єднання множин A і B позначають так: A B. Наприклад, (–3; 1) (0; 2] = (–3; 2], (–∞; 1) [–1; +∞) = (–∞; +∞). Об’єднання множин ірраціональних і раціональних чисел дорівнює множині дійсних чисел. Зауважимо, що A ∅ = A. З означення об’єднання двох множин випливає, що коли A ⊂ B, то A B = В, зокрема, якщо B = A, то A A = A. Наприклад, Q Z = Q, N R = R. Об’єднання множин зручно ілюструвати за допомогою діаграм Ейлера. На рисунку 6 заштрихована фігура зображує множину A B.

До уваги! Якщо треба знайти об’єднання множин розв’язків рівнянь (нерівностей), то кажуть, що треба розв’язати сукупність рівнянь (нерівностей). Сукупність записують за допомогою квадратної дужки. Так, щоб розв’язати рівняння (x2 – x) (x2 – 1) = 0, треба розв’язати сукупність рівнянь

Первинне закріплення вивченого матеріалу Яку множину називають підмножиною даної множини? Як наочно ілюструють співвідношення між множинами? Яка множина є підмножиною будь-якої множини? Що називають перетином двох множин? Що називають об’єднанням двох множин? Як за допомогою діаграм Ейлера ілюструють перетин (об’єднання) двох множин?

Усне виконання вправ 15.° Назвіть кілька підмножин учнів вашого класу. 16.° Назвіть які-небудь геометричні фігури, які є підмножинами множини точок прямої. 17.° Назвіть які-небудь геометричні фігури, які є підмножинами множини точок круга. 18.° Нехай A — множина букв у слові «координата». Множина букв якого слова є підмножиною множини A: кора; 4) крокодил; 7) тин; 10) дорога; дірка; 5) нитки; 8) криниця; 11) дар; картина; 6) нирки; 9) сокирка; 12) кардинал?

Тренувальні вправи (коментоване розв'язання) 20.° Нехай A ≠ ∅. Які дві різні підмножини завжди має множина A? 21.° Які з наступних тверджень є правильними: 1) {a} ∈ {a, b}; 2) {a} ⊂ {a, b}; 3) a ⊂ {a, b}; 4) {a, b} ∈ {a, b}? 22. Доведіть, що коли A ⊂ B і B ⊂ C, то A ⊂ C. 23. Розмістіть дані множини у такій послідовності, щоб кожна наступна множина була підмножиною попередньої: A — множина прямокутників; B — множина чотирикутників; C — множина квадратів; D — множина паралелограмів; A — множина ссавців; B — множина собачих; C — множина хребетних; D — множина вовків; E — множина хижих ссавців. 25. Запишіть усі підмножини множини {1, 2}. 27. Які з наступних тверджень є правильними: 1) {a, b} {a} = a; 2) {a, b} {a} = {a, b}; 3) {a, b} {a} = {a}; 4) {a, b} {a} = {b}? 28. Знайдіть перетин множин цифр, які використовуються в запису чисел: 1) 555288 і 82223; 2) 470713 і 400007. 30. Знайдіть множину спільних дільників чисел 30 і 45.

Тренувальні вправи (коментоване розв'язання) 31. Знайдіть перетин множин A і B, якщо: A — множина рівнобедрених трикутників, B — множина рівносторонніх трикутників; A — множина прямокутних трикутників, B — множина рівносторонніх трикутників; A — множина двоцифрових чисел, B — множина натураль- них чисел, кратних 19; A — множина одноцифрових чисел, B — множина простих чисел. 32. Накресліть два трикутники так, щоб їх перетином була така геометрична фігура: 1) відрізок; 2) точка; 3) трикутник; 4) п’ятикутник; 5) шестикутник. 34. Знайдіть: [–4; 6) (–2; 7); 2) (–∞; 3) (1; 4); 3) (–∞; 2) (3; 8]; 4) N (–3; 4]; (–2; 2) Z; 6) (–1; 1] [1; +∞); 7) (–1; 1] (1; +∞); 8) R (–2; 3). 36. Які з наступних тверджень є правильними: 1) {a, b} {b} = {a, b}; 2) {a, b} {b} = {b}; 3) {a, b} {a} = {a}; 4) {a, b} {b} = {{b}}? 37. Знайдіть об’єднання множин цифр, які використовуються в запису чисел: 1) 27288 і 56383; 2) 55555 і 777777. 38. Знайдіть об’єднання множин A і B, якщо: A — множина рівнобедрених трикутників, B — множина рівносторонніх трикутників; A — множина простих чисел, B — множина складених чисел; A — множина простих чисел, B — множина непарних чисел. 39. Накресліть два трикутники так, щоб їх об’єднанням був: чотирикутник; 2) трикутник; 3) шестикутник. Чи може об’єднання трикутників бути відрізком? 41. Знайдіть: 1) (–2; 5] (2; 7]; 2) (–∞; 3) (–3; 3]; 3) (–∞; 8) [–2; +∞); 4) R (–7; 2]; 5) Q N; 6)R N.

Вправи для повторення (алгоритми розв'язання)

Підсумки Вивчивши матеріал параграфа «Множини. Операції над множинами», ви дізналися, що: об’єкти, які складають множину, називають елементами цієї множини; дві множини A і B називають рівними, якщо вони складаються з одних і тих самих елементів, тобто кожний елемент множини A належить множині B і, навпаки, кожний елемент множини B належить множині A. Якщо множини A і B рівні, то пишуть A = B. Множина однозначно визначається своїми елементами. Якщо множину записують за допомогою фігурних дужок, то порядок, у якому виписано її елементи, не має значення; найчастіше множину задають одним із двох таких способів. Перший спосіб полягає в тому, що множину задають указанням (переліком) усіх її елементів. Другий спосіб полягає в тому, що задається характеристична властивість елементів множини, тобто властивість, яка притаманна всім елементам даної множини і тільки їм; множину, яка не містить жодного елемента, називають порожньою множиною і позначають символом ∅; множину B називають підмножиною множини A, якщо кожний елемент множини B є елементом множини A. Це записують так: B ⊂ A або A ⊃ B (читають: «множина B є підмножиною множини A» або «множина A містить множину B»); для ілюстрації співвідношень між множинами використовують схеми, які називають діаграмами Ейлера; коли A ⊂ B і B ⊂ A, то A = B; будь-яка множина A є підмножиною самої себе, тобто A ⊂ A; для будь-якої множини A справедливе твердження: ∅ ⊂ A; перетином множин A і B називають множину, яка складається з усіх елементів, що належать і множині A, і множині B. Перетин множин A і B позначають так: A B;

Підсумки якщо множини A і B не мають спільних елементів, то їх перетином є порожня множина, тобто A B = ∅. Також A ∅ = ∅; Коли A ⊂ B, то A B = A, зокрема, якщо B = A, то A A = A; об’єднанням множин A і B називають множину, яка складається з усіх елементів, що належать хоча б одній з цих множин: або множині A, або множині B. Об’єднання множин A і B позначають так: A B; A ∅ = A; коли A ⊂ B, то A B = В, зокрема, якщо B = A, то A A = A; якщо треба знайти об’єднання множин розв’язків рівнянь (нерівностей), то кажуть, що треба розв’язати сукупність рівнянь (нерівностей). Сукупність записують за допомогою квадратної дужки.

Завдання додому Прочитати п.1-2 Вивчити означення та властивості Виконати вправи: 19, 24, 26, 29, 33, 35, 40, 42 За складеними на уроці алгоритмами розв'язування вправ виконати завдання у зошиті: 43, 44, 45 (на вибір)