Презентація на тему:
Поняття множини. Операції над множинами

Тема №1 Поняття множини. Операції над множинами.

Якщо В може і дорівнювати А, то вживається символ А В Належність предмета даній множині позначається символом , а неналежність – символом Множини бувають скінченні і нескінченні Множина, в якій немає жодного елемента, називається порожньою і позначається символом Якщо множина В складається з деяких елементів даної множини А (і тільки з них), то множина В називається підмножиною множини А. Позначається В А Наприклад, число 8 А, де А- множина дільників числа 24, а число 11 А. А В

Поняття про нескінченну множину, ввійшовши до складу сучасної математики, радикально еволюціонувало її. П.С. Александров Поняття множини належить до первісних понять математики, якому не дається означення. Множину можна уявити як сукупність, зібрання деяких предметів, об’єднаних за певною характеристичною ознакою. Предмети, з яких складається множина, називаються її елементами і позначаються малими літерами латинського алфавіту. Для позначення множин використовують великі літери латинського алфавіту або фігурні дужки, всередині яких записуються елементи множини. При цьому порядок запису елементів не має значення. Наприклад, множину всіх дільників числа 24 можна позначити літерою А (чи будь-якою великою літерою латинського алфавіту) або записати так

Множину задають такими основними способами: переліком всіх її елементів, описом характеристичної властивості її елементів. Наприклад: - множина , задана переліком елементів. М- множина всіх дільників числа 16, задана вказівкою характеристичної властивості. Цю саму множину можна задати і переліком її елементів: . Дві множини називаються рівними, якщо вони складаються з тих самих елементів. Наприклад, множини коренів рівняння і

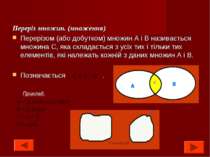
Переріз множин. (множення) Перерізом (або добутком) множин А і В називається множина С, яка складається з усіх тих і тільки тих елементів, які належать кожній з даних множин А і В. Позначається . Приклад.

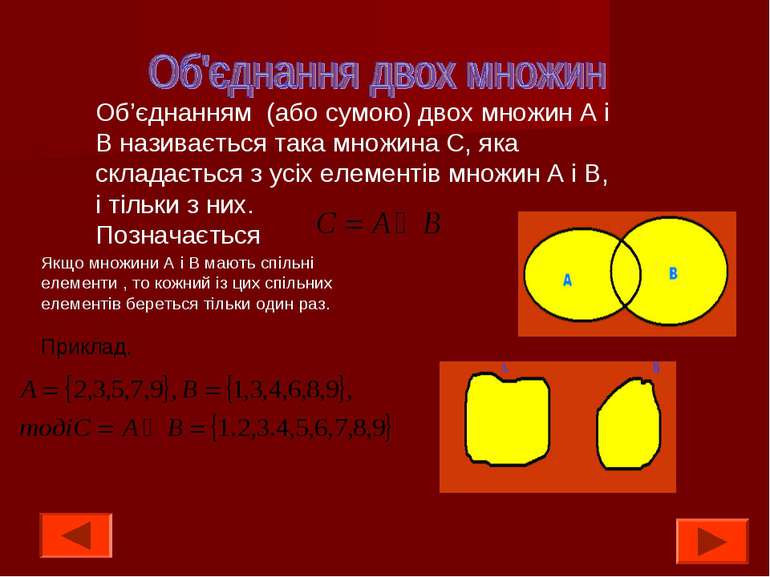
Об’єднанням (або сумою) двох множин А і В називається така множина С, яка складається з усіх елементів множин А і В, і тільки з них. Позначається Якщо множини А і В мають спільні елементи , то кожний із цих спільних елементів береться тільки один раз. Приклад.

Різниця множин. Різницею двох множин А і В називається така множина С , яка складається з усіх елементів множини А, які не належать множині В. Позначається А\В. Приклад.

У випадку, якщо В – частина множини А , то називається доповненням до В у множині А і позначають . В

Запитання для повторення 1. Навести приклади множин. 2. Які бувають множини за кількістю елементів? Як вони позначаються? 3. Як позначаються належність і неналежність елемента певній множині? 4. Якими способами задаються множини? Навести приклади. 5. Які множини називаються рівними? Навести приклади. 6. Яка множина називається підмножиною даної множини. Навести приклади. 7. Які операції над множинами ви знаєте?