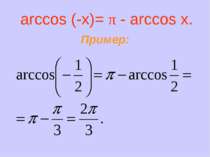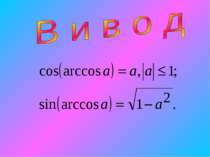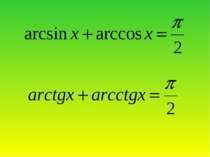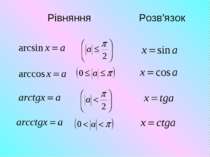Презентація на тему:
Обернені тригонометричні функції
Завантажити презентацію
Обернені тригонометричні функції
Завантажити презентаціюПрезентація по слайдам:
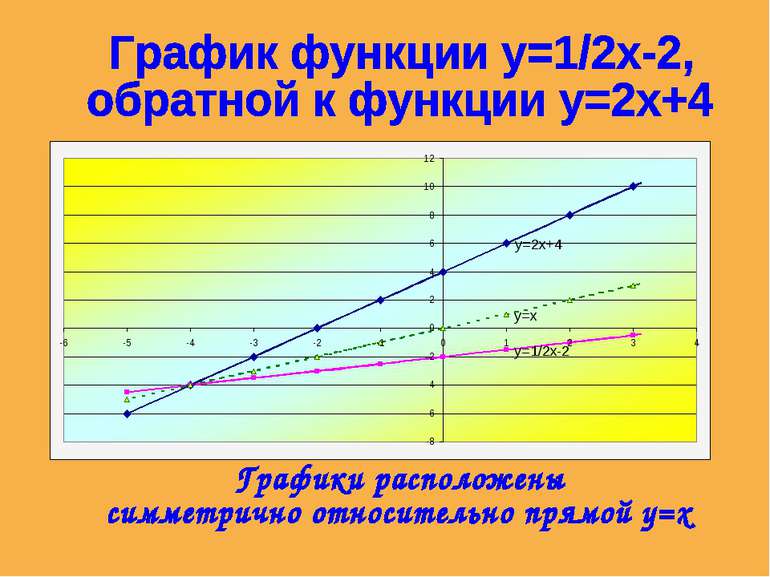
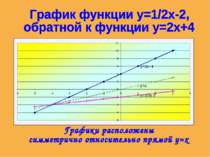
Обратной называется функция, которая принимает свое значение в единственной точке области опрелеления.
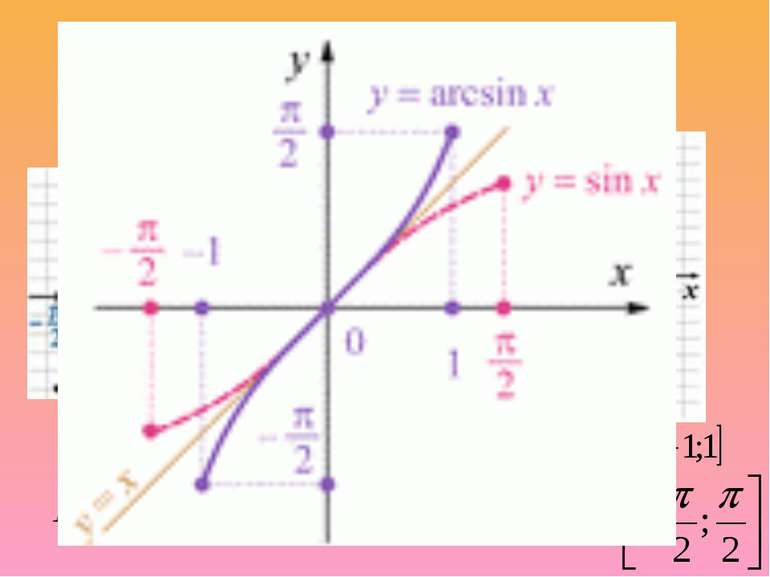
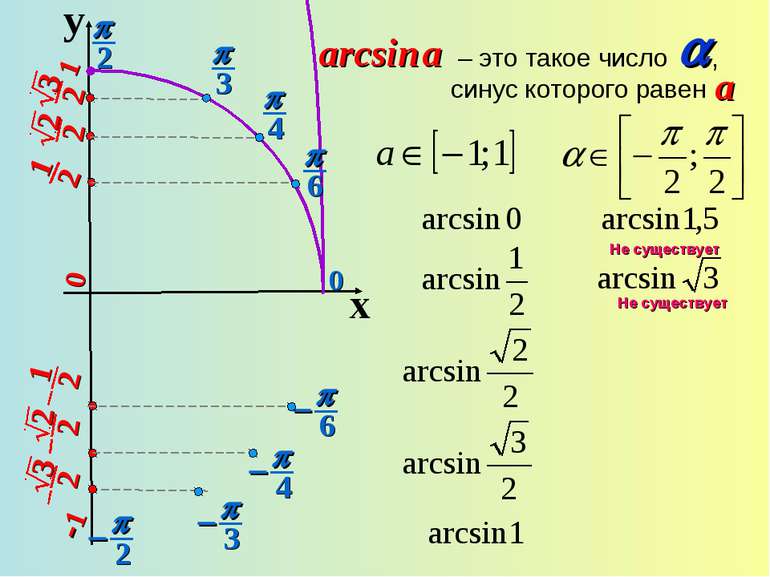
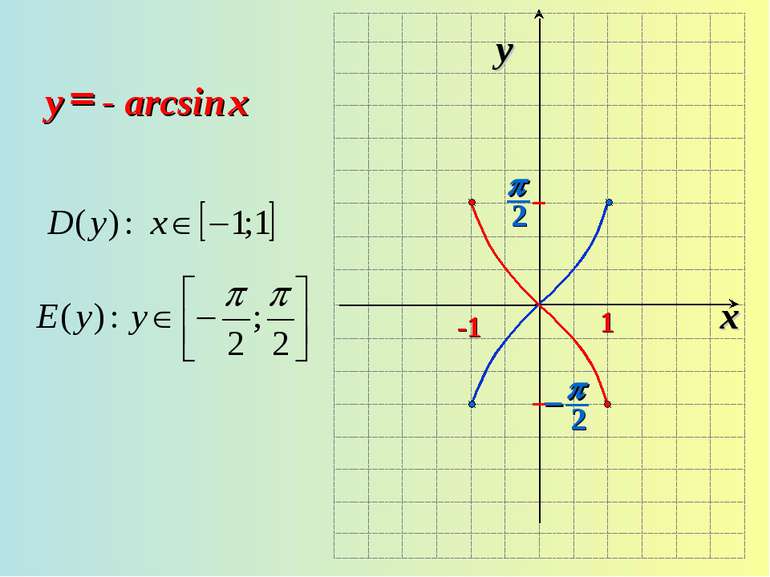
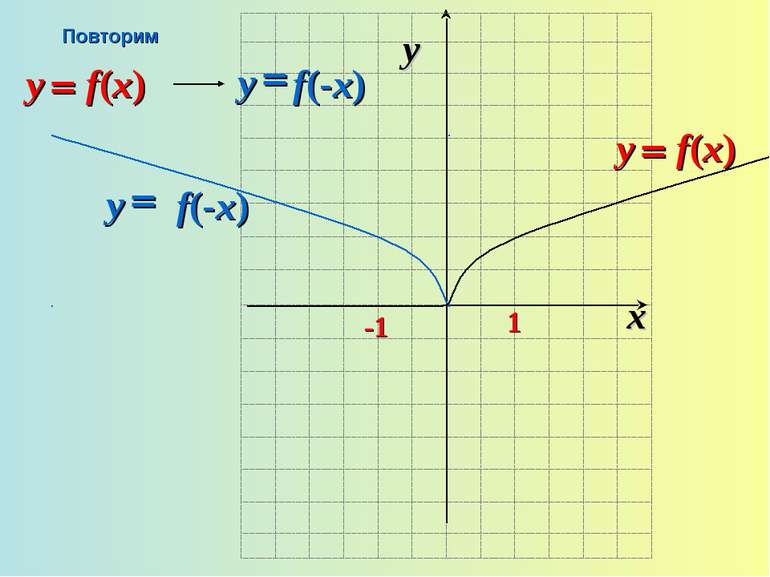
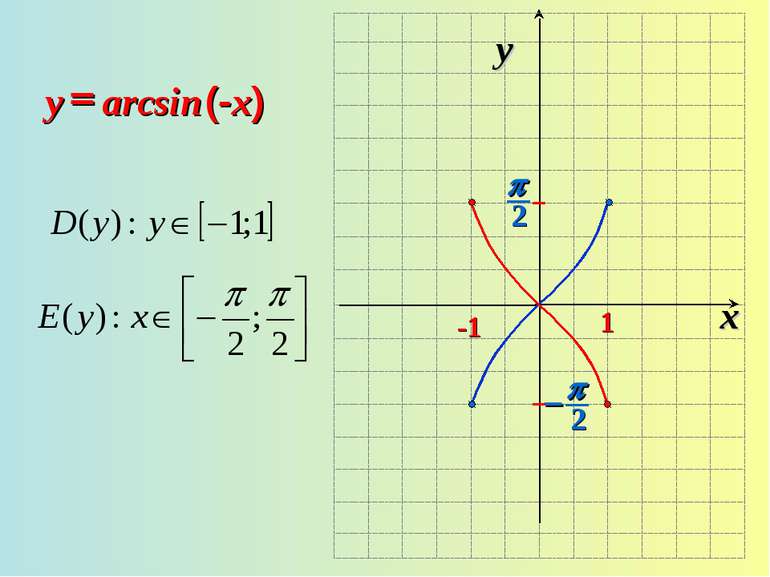
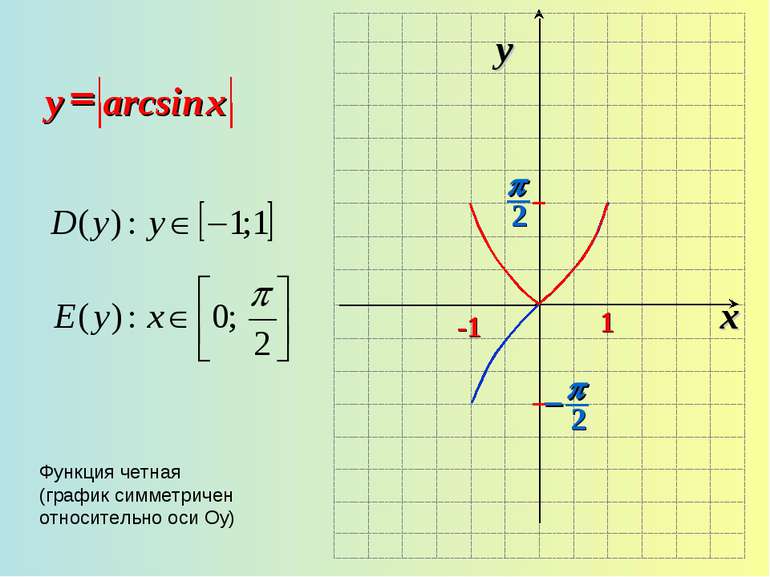
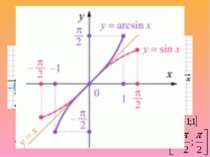
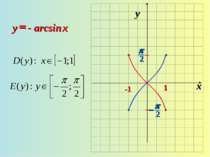
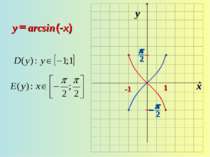
3. Графік симметричен относительно начала координат (функция нечетная) arcsin (-x)=-arcsin x. 4. Функция возрастающая. Если х1>x2, то arcsin x1 > arcsin x2. 5. у = 0, если х = 0.
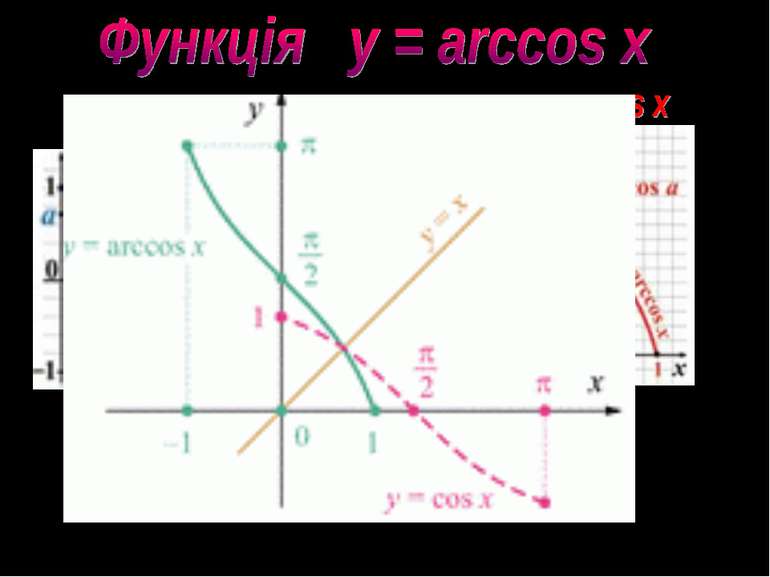
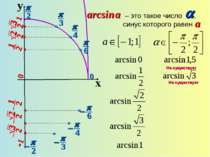
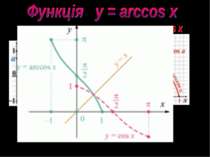
3. График не симметричен ни относительно начала координат, ни относительно оси OY. arccos (-x)=π-arccos x. 4. Функция убывающая. Если х1>x2, то arccos x1 < arccos x2. 5. у = 0, если х = 1.
Арккосинусом числа а называется такое число из промежутка [0; π], косинус которого равен а. Приклад:
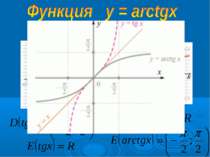
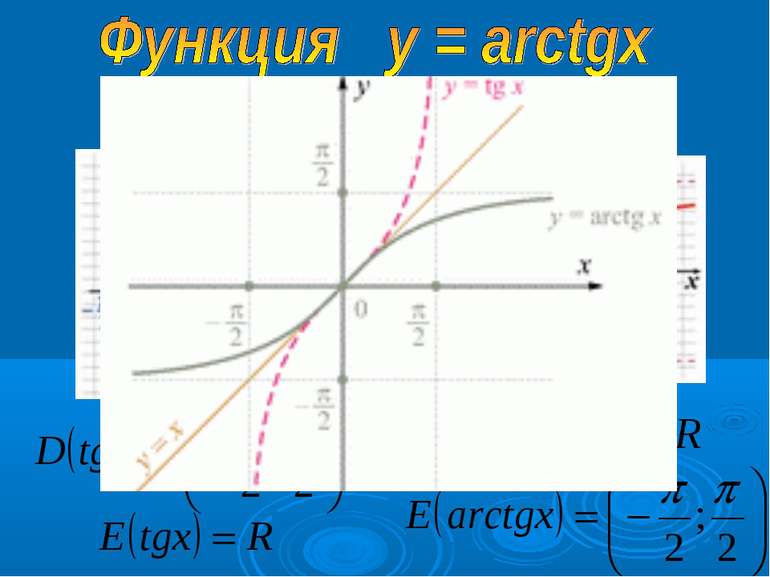
3. График симметричен относительно начала координат, функция нечетная: arctg (-x)= -arctg x. 4. Функция возростающая если х1>x2, то arctg x1 > arctg x2. 5. у = 0, якщо х = 0. 6. у > 0, якщо х > 0; у < 0, якщо х < 0 1. D (arctg) = R 2. E (arctg) = ( -π/2; π/2)
Арктангенсом числа а называется число из промежутка ( -π/2; π/2), тангенс которого равен а. Пример:
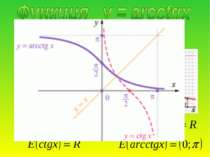
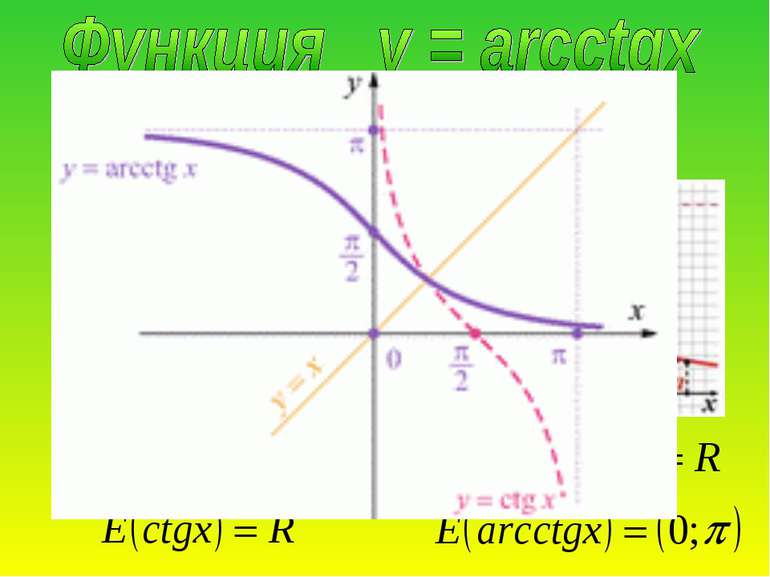
1. D (arcсtg) = R 2. E (arcсtg) = ( 0; π) 3. График не симметричный ни относительно начала координат, ни относительно оси ОУarcctg (-x)= π -arctg x. 4. Функція спадна. Якщо х1>x2, то arcctg x1 < arcctg x2. 5. x = 0, якщо y = π/2 . 6. у > 0 для всіх х
Арккотангенсом числа а називається таке число із інтервала ( 0; π), котангенс якого дорівнює а. Приклад:
1. Обчисліть: 2. Знайдіть область визначення функції: 3. Знайдіть область визначення функції:
Схожі презентації
Категорії







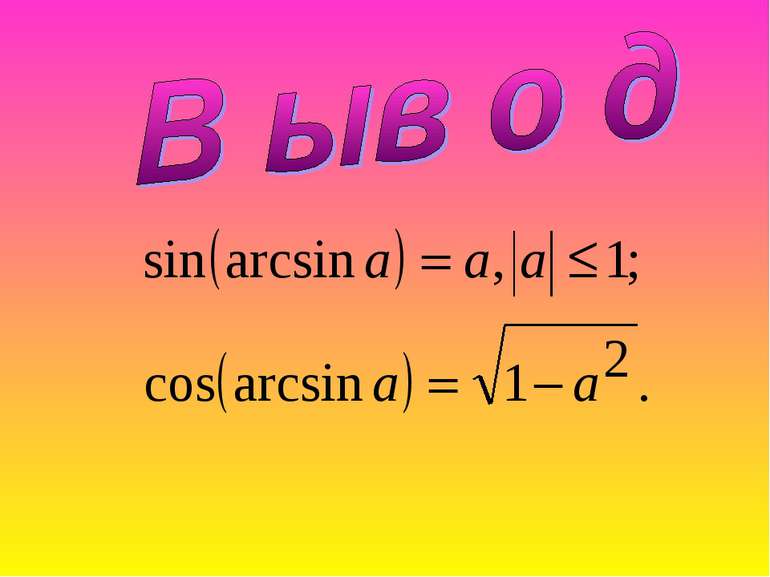




![Арккосинусом числа а называется такое число из промежутка [0; π], косинус кот... Арккосинусом числа а называется такое число из промежутка [0; π], косинус кот...](https://svitppt.com.ua/images/34/33106/770/img20.jpg)
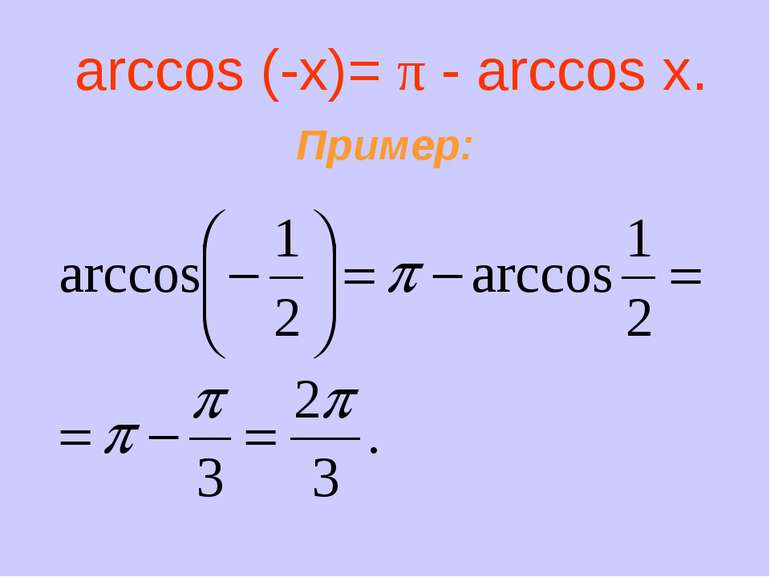


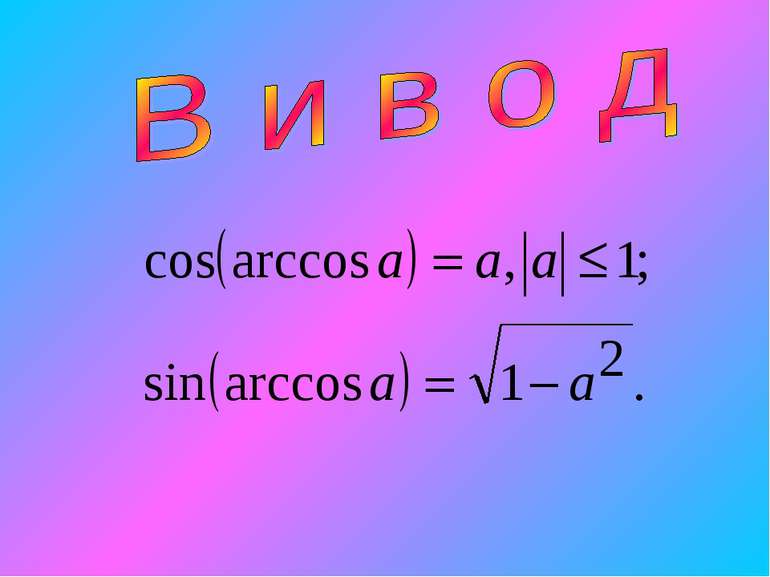






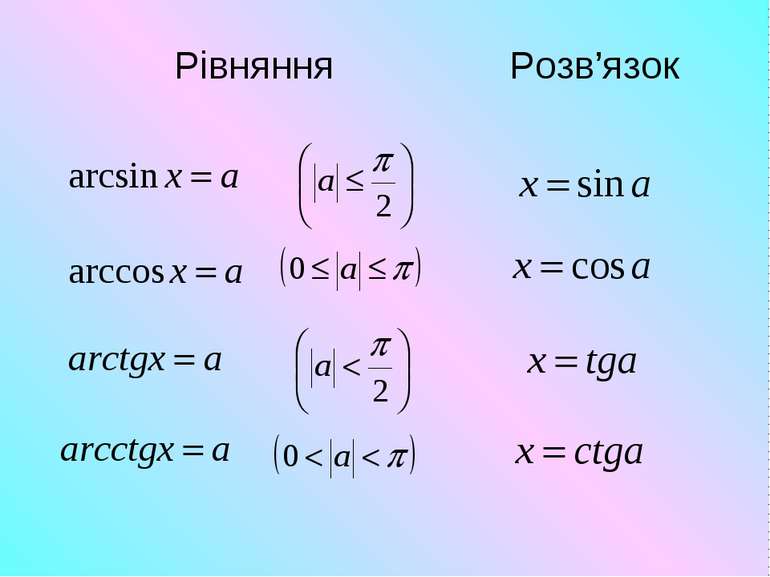







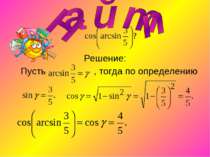
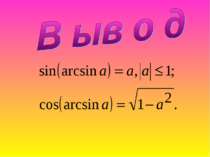




![Арккосинусом числа а называется такое число из промежутка [0; π], косинус кот... Арккосинусом числа а называется такое число из промежутка [0; π], косинус кот...](https://svitppt.com.ua/images/34/33106/210/img20.jpg)