Презентація на тему:
Навчальний посібник

Навчальний посібник Україна Чернігівська область село Манжосівка вулиця Шкільна, 5 телефон (04637) Дідівська загальноосвітня школа І – ІІІ ступенів

Алгебра, 7 клас Прилуцька загальноосвітня школа І – ІІІ ступенів № 10 Розв"язування систем лінійних рівнянь

Алгебра стоїть на чотирьох китах Число Рівняння Тотожність Функція

Означення Рівняння – це рівність, яка має одну або кілька змінних Лінійне рівняння з однією змінною Лінійне рівняння з двома змінними Властивості рівнянь Якщо в рівнянні перенести доданок з однієї частини в другу, змінивши його знак, то одержимо рівняння , рівносильне даному Якщо обидві частини рівняння помножити або поділити на одне і те ж, відмінне від нуля число, то одержимо рівняння, рівносильне даному Рівняння і його властивості

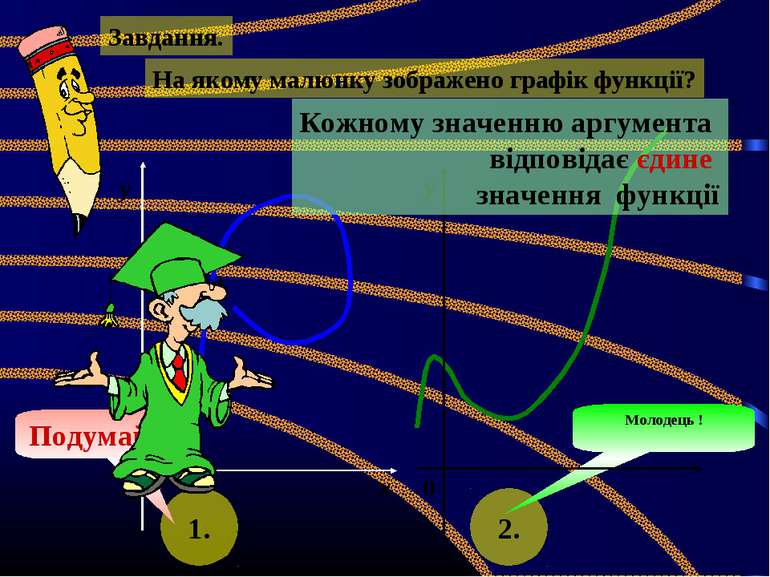
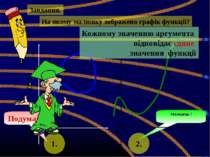
Завдання. На якому малюнку зображено графік функції? х у 0 у 1. 2. Подумай! Молодець ! Кожному значенню аргумента відповідає єдине значення функції

Система рівнянь і її розв”язування Означення Системою рівнянь називається деяка кількість рівнянь, об’єднаних фігурною дужкою. Фігурна дужка означає, що всі рівняння повинні виконуватися одночасно. Кожна пара змінних, яка одночасно є розв'язком всіх рівнянь системи, називається розв'язком системи Розв'язком системи двох рівнянь з двома змінними називається пара значень змінних, яка перетворює кожне рівняння системи в правильну рівність Розв'язати систему рівнянь – це значить знайти всі її розв'язки або встановити, що їх немає

Способи розв'язування систем рівнянь Способи розв’язування Система лінійних рівнянь а1х+b1y=c1 а2х+b2y=c2, де а1, а2, b1, b2, c1, c2 задані числа, а х і у невідомі Спосіб підстановки Спосіб порівняння Спосіб додавання Графічний спосіб Метод визначників

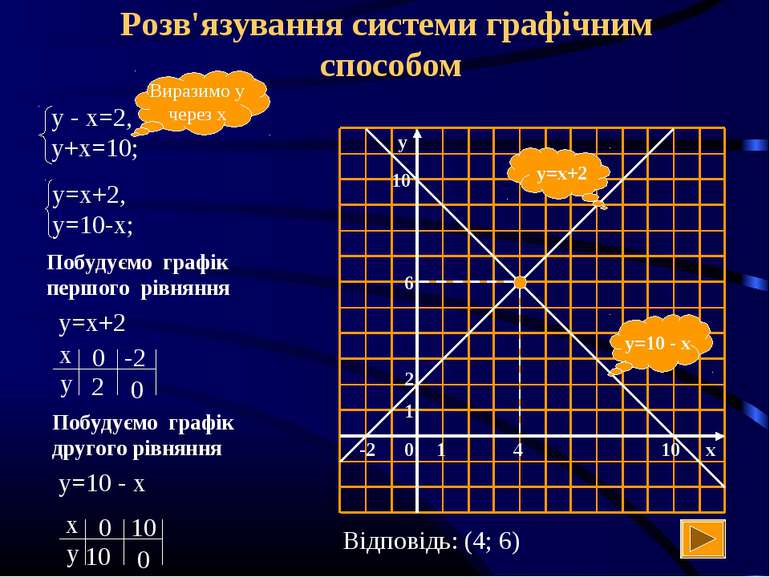
Розв'язування системи графічним способом y=10 - x y=x+2 Виразимо у через х Побудуємо графік першого рівняння у=х+2 Побудуємо графік другого рівняння у=10 - х Відповідь: (4; 6)

Графічний спосіб (алгоритм) Виразити у через х в кожному рівнянні Побудувати в одній системі координат графік кожного рівняння Визначити координати точки перетину Записати відповідь: х=…; у=… , або (х; у)

Розв"язування системи способом підстановки 7х - 2х - 4 = 1; 5х = 5; х=1; Відповідь : х=1; у=6.

Спосіб підстановки (алгоритм) З якого-небудь рівняння виразити одну змінну через іншу Підставити одержаний вираз для змінної в друге рівняння і розвязати його Зробити підстановку одного значення змінної і обчислити значення другої змінної Записати відповідь: х=…; у=… .

Розв”язування системи способом порівняння Прирівняєм вирази для у 7х - 1=2х+4, 7х - 2х=4+1, 5х=5, х=1. Розв'яжемо рівняння Відповідь: (1; 6)

Спосіб порівняння (алгоритм) Виразити у через х (або х через у) в кожному рівнянні Прирівняти вирази, одержані для однойменних змінних Розв'язати одержане рівняння і знайти значення однієї змінної Підставити значення знайденої змінної в один з виразів для іншої змінної і знайти її значення Записати відповідь: х=…; у=… .

Розв”язування системи способом додавання ||·(-3) + ____________ Відповідь: (3; - 10)

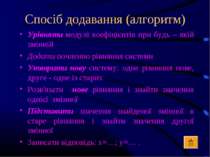
Спосіб додавання (алгоритм) Урівняти модулі коефіцієнтів при будь – якій змінній Додати почленно рівняння системи Утворити нову систему: одне рівняння нове, друге - одне із старих Розв'язати нове рівняння і знайти значення однієї змінної Підставити значення знайденої змінної в старе рівняння і знайти значення другої змінної Записати відповідь: х=…; у=… .

-80 Розв'язування системи методом визначників Складемо матрицю із коефіцієнтів при невідомих = 7·6 - 2·17 = 42 - 34 = 8 = 1·6 - 2·(-9) = 6 + 18 = 24 = 7·(-9) - 1·17 = - 63 -17= -80 Складемо визначник x, замінивши у визначнику перший стовпчик на стовпчик вільних членів Складемо визначник y, замінивши у визначнику другий стовпчик на стовпчик вільних членів x х= = 24 8 = 3; у= y = 8 = -10. Знайдемо х і у Відповідь: х=3; у= -10.

Метод визначників (алгоритм) Складемо табличку (матрицю) коефіцієнтів невідомих і обчислимо визначник . Знайдемо визначник x, одержаний із заміною першого стовпчика на стовпчик вільних членів. Знайдемо визначник y, одержаний із заміною другого стовпчика на стовпчик вільних членів. Знайти значення змінної х за формулою x / . Знайти значення змінної у за формулою y / . Записати відповідь: х=…; у=… .