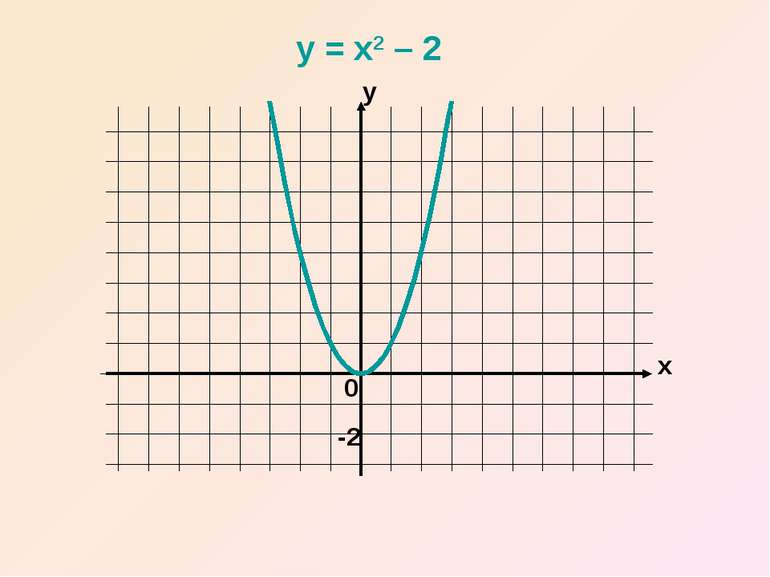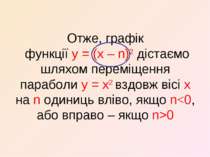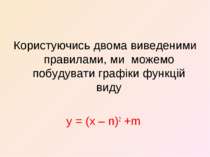Презентація на тему:
Графік квадратичної функції

Побудова графіка квадратичної функції y = x2 + bx + c

Квадратичною функцією називається функція, яку можна задати формулою виду y = ax² + bx + c, де х – незалежна змінна, a,b,c - деякі числа, причому a ≠ 0. Графіком квадратичної функції є парабола

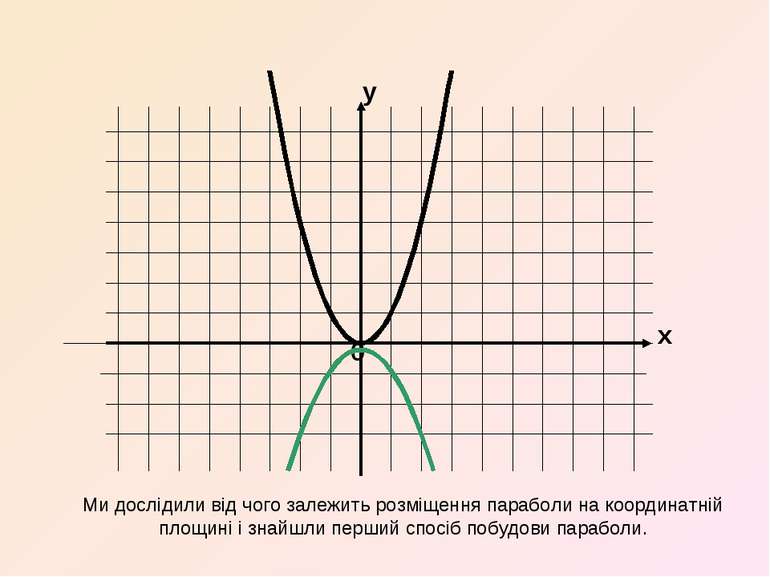
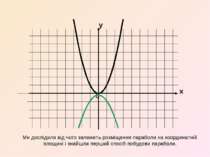
x y 0 Ми дослідили від чого залежить розміщення параболи на координатній площині і знайшли перший спосіб побудови параболи.

Алгоритм побудови параболи f(x) = ax² + bx + c Напрям віток. Вершина ( x = -b ∕ 2a; y = f(x ). ) Вісь симметрії. Таблиця значень. Побудова графіка.

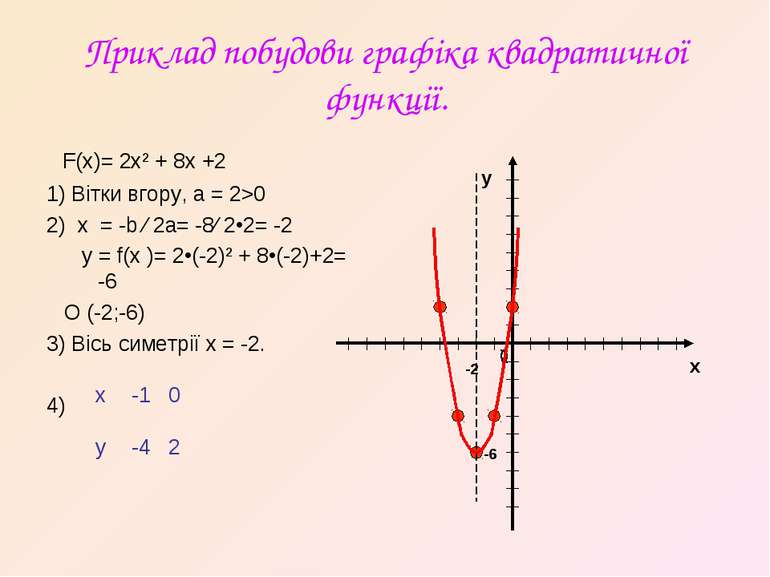
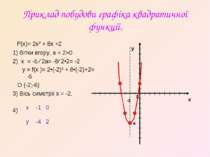
Приклад побудови графіка квадратичної функції. F(x)= 2x² + 8x +2 1) Вітки вгору, а = 2>0 2) х = -b ∕ 2a= -8∕ 2•2= -2 y = f(x )= 2•(-2)² + 8•(-2)+2= -6 O (-2;-6) 3) Вісь симетрії х = -2. 4) у х -2 -6

Щоб знайти цей спосіб, визначимо шляхи переміщення параболи y = x2 + bx + c Чи існує інший спосіб побудови графіка квадратичної функції? Відповідь – так!

x y 0 y = x2 + 3 3

x y 0 y = x2 – 2 -2

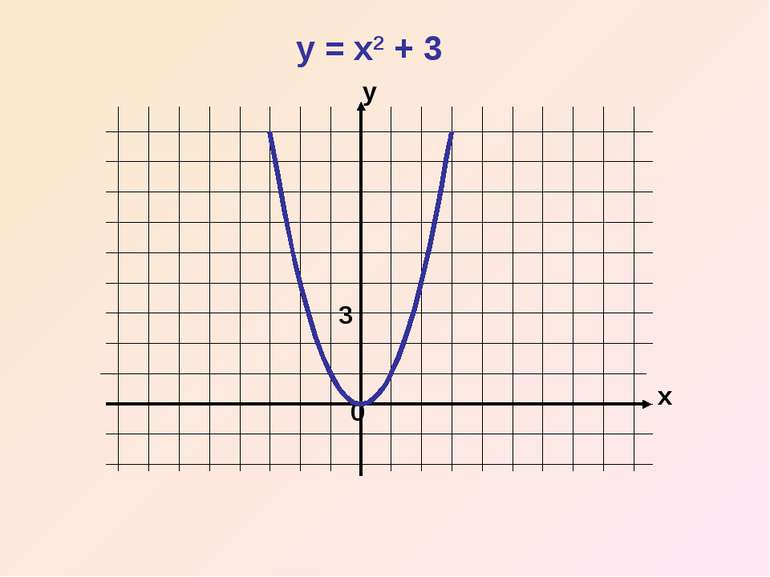
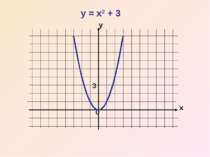
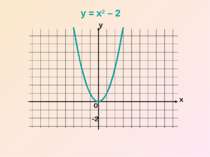
Таким чином, графік функції y = x2 + m можна дістати шляхом переміщення параболи y = x2 вздовж вісі y на m одиниць вгору , якщо m>0, або вниз – якщо m

x y -4 y = (x+4)2 0

x y 0 y = (x-5)2 5

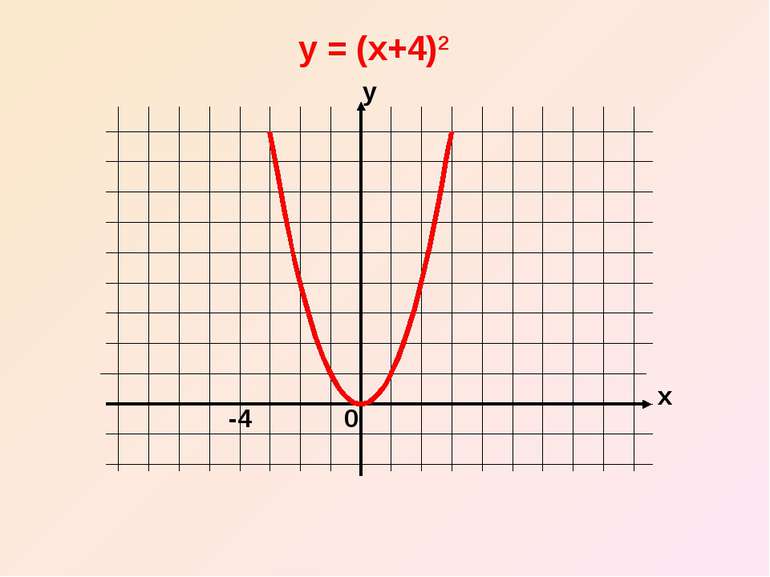
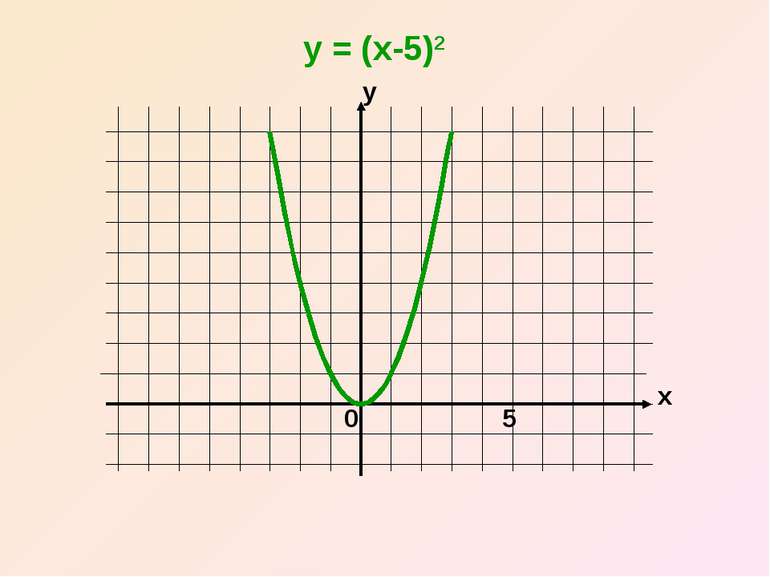
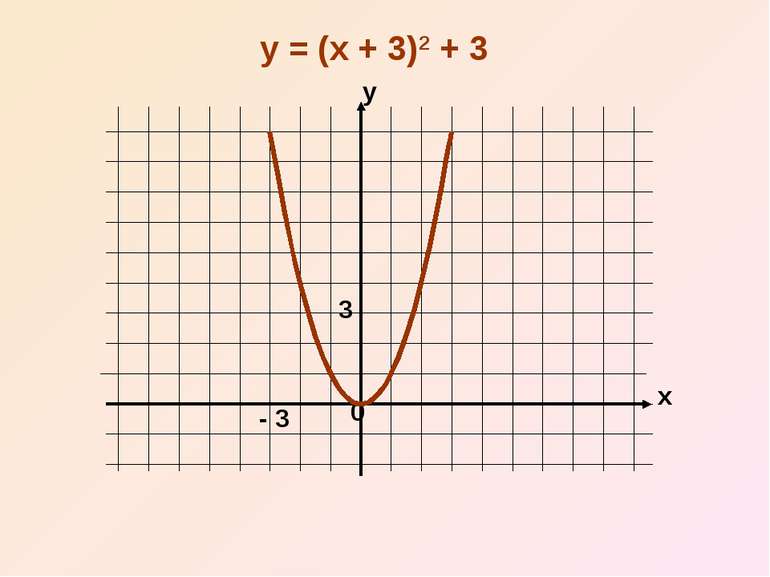
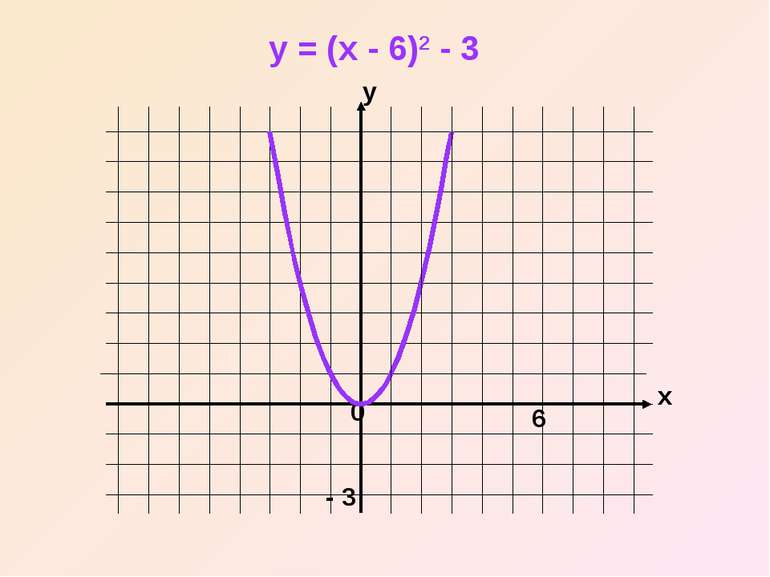
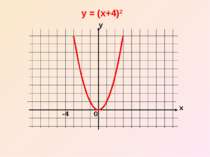
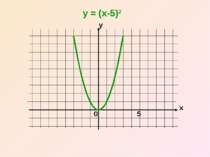
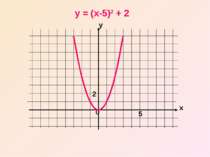
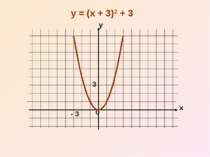
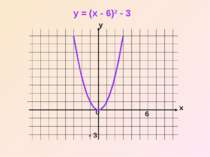
Отже, графік функції y = (x – n)2 дістаємо шляхом переміщення параболи y = x2 вздовж вісі x на n одиниць вліво, якщо n0

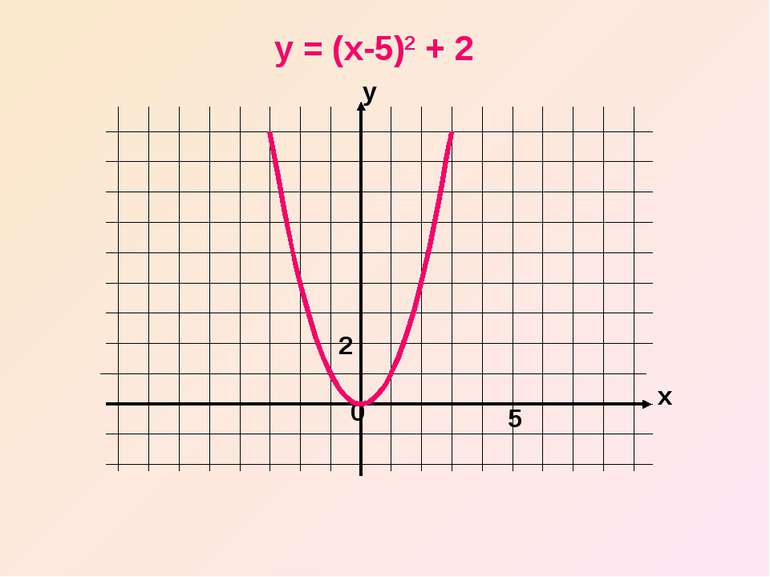
Користуючись двома виведеними правилами, ми можемо побудувати графіки функцій виду у = (x – n)2 +m

x y 0 y = (x-5)2 + 2 5 2

x y 0 y = (x + 3)2 + 3 - 3 3

x y 0 y = (x - 6)2 - 3 - 3 6

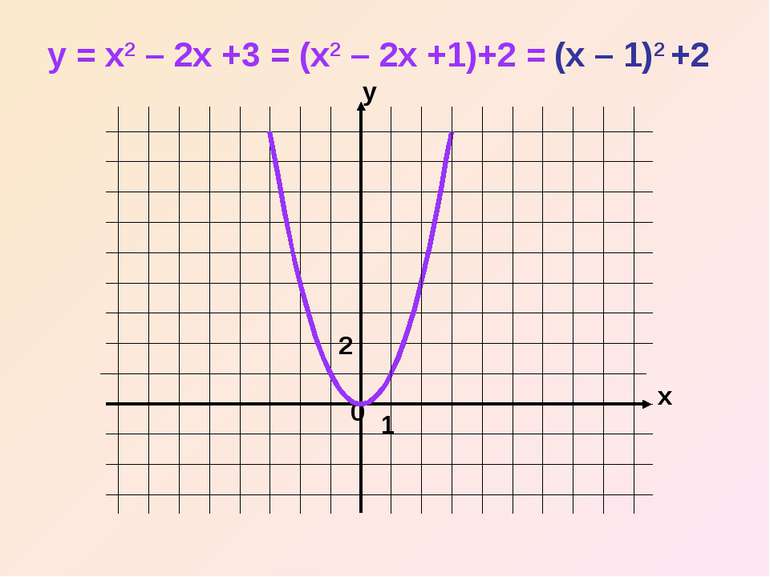
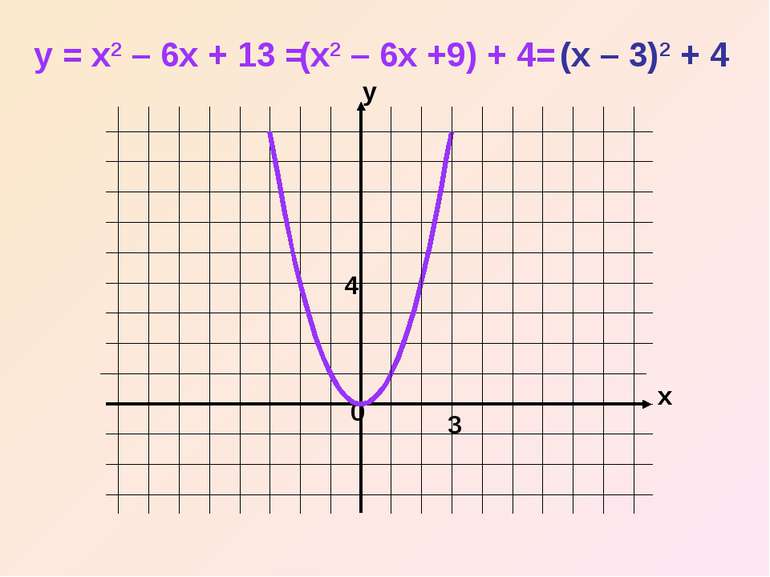
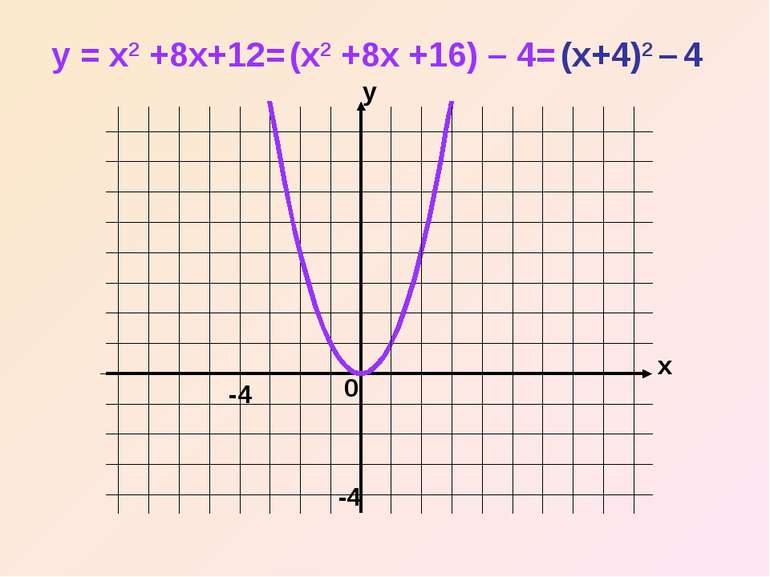
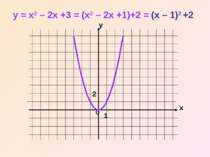
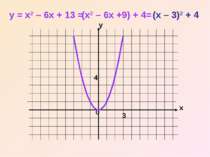
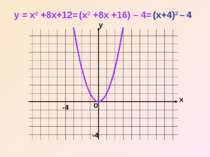
Щоб побудувати графік функції y = x2 + bx + c за допомогою елементарних перетворень, треба: 1) виділити в формулі функції квадрат двочлена; 2) побудувати графік за допомогою правил переміщення графіків.

x y 0 y = x2 – 2x +3 = (x2 – 2x +1)+2 = (x – 1)2 +2 1 2

x y 0 y = x2 – 6x + 13 = (x2 – 6x +9) + 4= (x – 3)2 + 4 3 4

x y 0 y = x2 +8x+12= (x2 +8x +16) – 4= (x+4)2 – 4 -4 -4

Дякуємо за увагу!