Презентація на тему:
Використання інтеграла для обчислення площ
Завантажити презентацію
Використання інтеграла для обчислення площ
Завантажити презентаціюПрезентація по слайдам:
Використання інтеграла для обчислення площ..
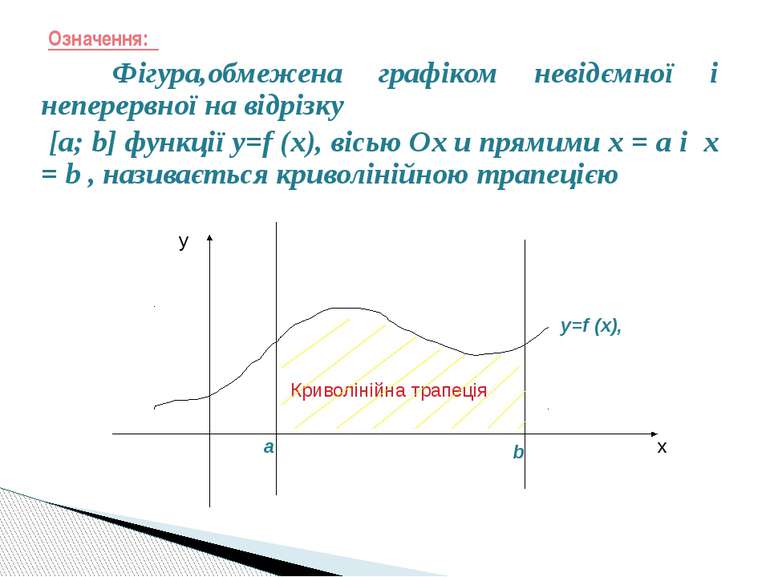
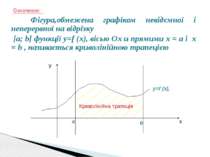
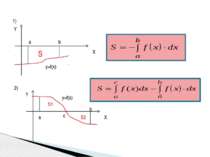
Означення: Фігура,обмежена графіком невідємної і неперервної на відрізку [a; b] функції y=f (x), вісью Ох и прямими х = а і х = b , називається криволінійною трапецією x y y=f (x), а b Криволінійна трапеція
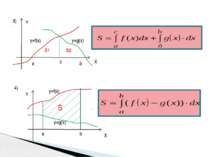
Теорема: Визначений інтеграл від a до b функції f(x) рівний площі S відповідної криволінійної трапеції : Y X а b y=f(x) B C S
a b y=f(x) S 1) 2) y=f(x) a b c S1 S2 Y X Y X
Y X a b y=f(x) 3) 4) Y X y=f(x) a b c S1 S2 y=g(x) y=g(x) S
x y 2 5
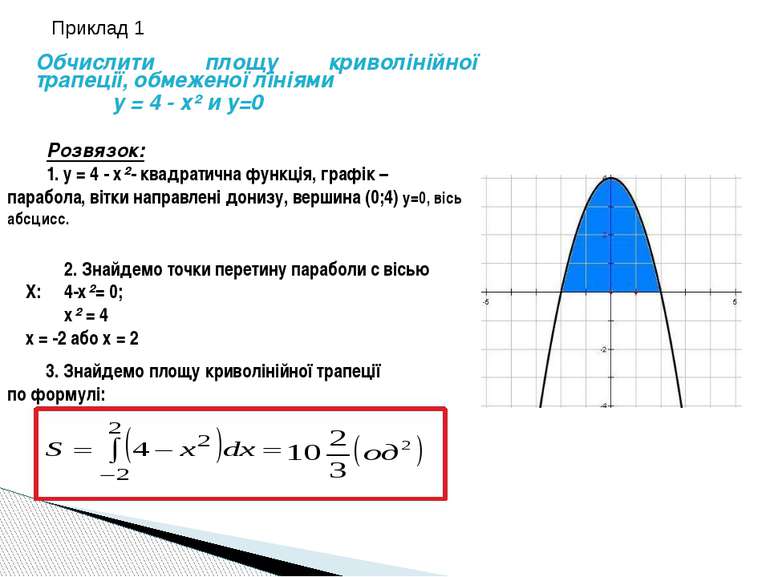
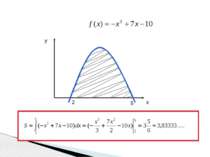
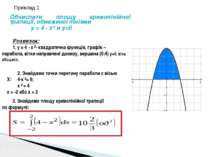
Обчислити площу криволінійної трапеції, обмеженої лініями у = 4 - х² и у=0 Розвязок: 1. у = 4 - х²- квадратична функція, графік – парабола, вітки направлені донизу, вершина (0;4) у=0, вісь абсцисс. 2. Знайдемо точки перетину параболи с вісью Х: 4-х²= 0; х² = 4 х = -2 або х = 2 3. Знайдемо площу криволінійної трапеції по формулі: Приклад 1
Схожі презентації
Категорії
