Презентація на тему:
Піраміда Означення та властивост

Піраміда Означення та властивості {

ПІРАМІДОЮ називається многогранник, одна грань якого – довільний многокутник, а інші грані – трикутники, що мають спільну вершину

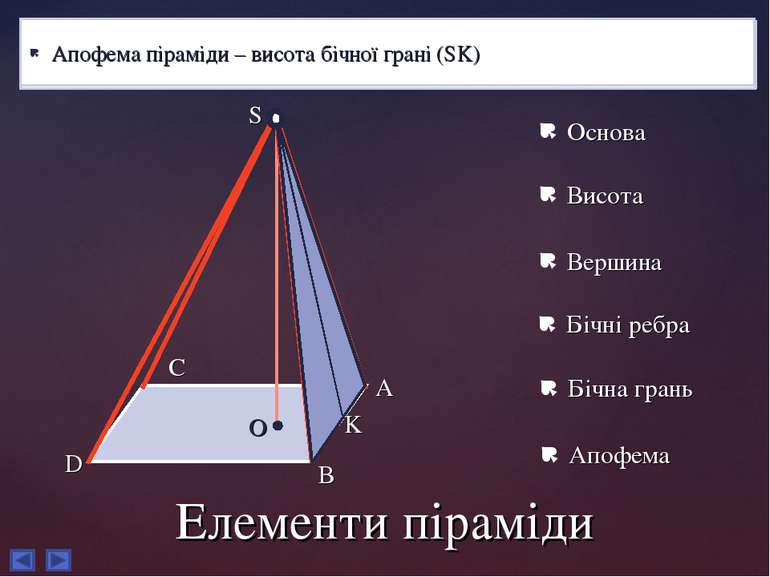
Елементи піраміди Основа піраміди – довільний многокутник, над площиною якого розміщено вершину піраміди (ABCD) Висота піраміди – перпендикуляр, опущений з вершини піраміди на основу (SO) Вершина піраміди – точка, розташована на висоті піраміди, яка проектується на основу цієї піраміди (S) Бічні ребра – Відрізки, що сполучають вершину піраміди з вершинами основи (SA, SB, SC, SD) Бічні грані – трикутники, що мають спільну вершину та утворюють бічну поверхню піраміди (ASB, BSC, CSD, DSA) Апофема піраміди – висота бічної грані (SK) Основа Висота Вершина Бічні ребра Бічна грань Апофема S O A B C D K

Формули площі піраміди

Формула площі правильної зрізаної піраміди

Тест «Перевір себе…» Яке найменше число граней може бути у піраміди? а) 2 б) 3 в) 4 Неправильно Правильно Чи існує піраміда, яка має 125 ребер? а) Існує б) Не існує Неправильно Правильно Чи існує піраміда, яка має 125 граней? а) Існує б) Не існує Правильно Неправильно Чи може піраміда мати дві бічні грані, які перпендикулярні до основи? а) Може б) Не може Правильно Неправильно Чи може піраміда мати три бічні грані, які перпендикулярні до основи а) Може б) Не може Неправильно Правильно Неправильно

Піраміда може мати два бічні ребра перпендикулярні до основи а) Так б) Ні Неправильно Правильно Тест «Перевір себе…» Існує піраміда, яка має 18 плоских кутів а) Існує б) Не існує Неправильно Правильно Тетраедр – це піраміда? а) Так б) Ні Неправильно Правильно Чи є піраміда тетраедром? а) Так б) Ні Неправильно Правильно Якщо одна з бічних граней піраміди перпендикулярна до основи, то висота піраміди збігається з висотою даної грані? а) Так б) Ні Неправильно Правильно

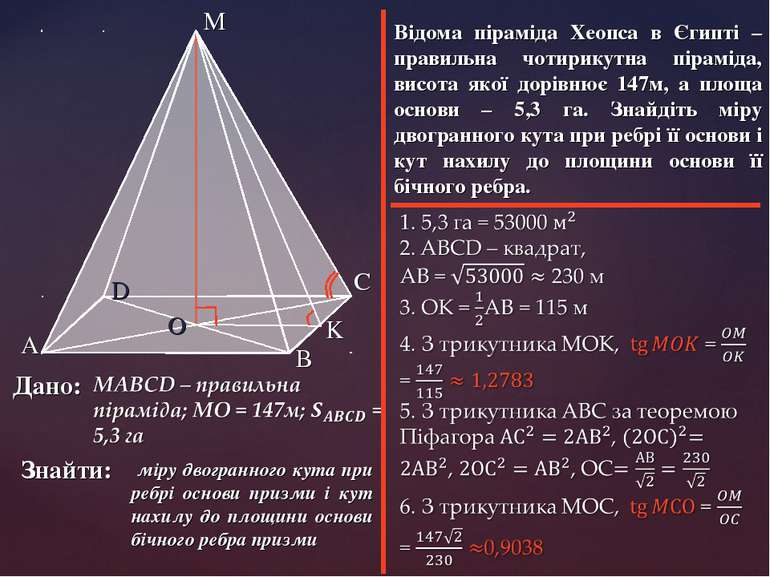
Відома піраміда Хеопса в Єгипті – правильна чотирикутна піраміда, висота якої дорівнює 147м, а площа основи – 5,3 га. Знайдіть міру двогранного кута при ребрі її основи і кут нахилу до площини основи її бічного ребра. Дано: Знайти: міру двогранного кута при ребрі основи призми і кут нахилу до площини основи бічного ребра призми K