Презентація на тему:
Випадкові похибки

Л3 Випадкові похибки

1.Випадкові похибки 2.Числові характеристики випадкових похибок 3.Типові моделі густини розподілу випадкової похибки

1.Випадкові похибки

Випадкові похибки - це похибки, що змінюються в часі нерегулярно, непередбачувано, а їх майбутні значення можна прогнозувати лише певною часткою ймовірності.

Випадкові похибки є частиною загальної (сумарної) похибки Δ∑, що в загальному випадку складається з суми випадкових ∑ ΔВ та суми систематичних ∑ Δ С похибок: Δ∑ =Σ ΔiВ +Σ ΔkС

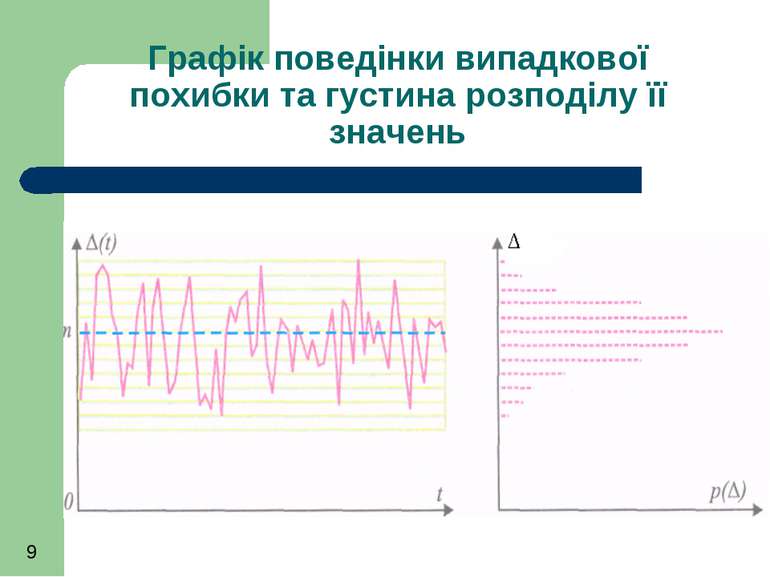
Результати вимірювань спотворені випадковим похибками, змінюються хаотично. На практиці буває важко відразу відрізнити випадкову похибку від змінної регулярної, наприклад, періодичної.

Незважаючи на хаотичність змін чергових значень випадкових похибок, для них характерна стабільність певних, усереднених в часі, властивостей, наприклад, частоти появи тих чи інших значень, середнього та середнього квадратичного значень, статистичного взаємозв'язку між значеннями через певний інтервал часу тощо.

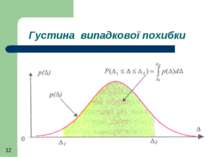
Однією з найважливіших характеристик випадкової похибки є її густина (закон, щільність) розподілу значень р(∆). Вона характеризує частість появи тих чи інших значень похибки.

Графік поведінки випадкової похибки та густина розподілу її значень

Залежно від того, які значення може набувати похибка, густина розподілу може бути неперервною або дискретною (квантованою за значенням) функцією. При квантуванні випадкової похибки кількість значень, що потрапили до одного кванта, віднесена до загальної кількості результатів, є оцінкою ймовірності появи похибки певного значення

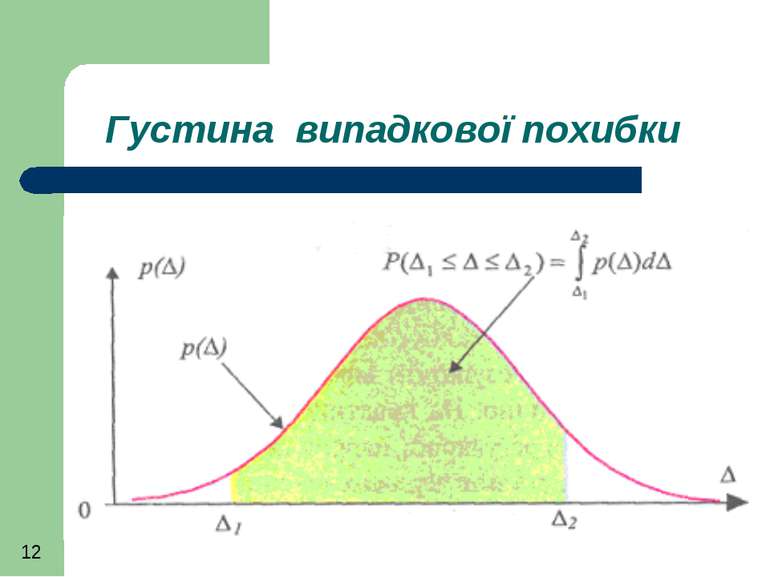
Для неперервної інтенсивності значень випадкової похибки її густина розподілу не є ймовірністю, але за її допомогою можна встановити імовірність Р того, що похибка потрапить у певний інтервал ∆1 ≤ ∆ ≤ ∆2 (подібно до того, як питома густина матеріалу якогось об'єкта не є масою, але дає можливість визначити масу конкретної частини об'єму цього об'єкта).

Густина випадкової похибки

Ймовірність появи похибки в інтервалі ∆1 ≤ ∆ ≤ ∆2 Для цього потрібно проінтегрувати густину розподілу в межах заданого інтервалу (що є площею криволінійної трапеції)

Оскільки ймовірність появи якоїсь події не може бути від'ємною, а також більшою за 1 (чи 100 %), то густина розподілу - є невід'ємною функцією: - площа під її кривою (інтеграл у нескінченних межах) дорівнює одиниці:

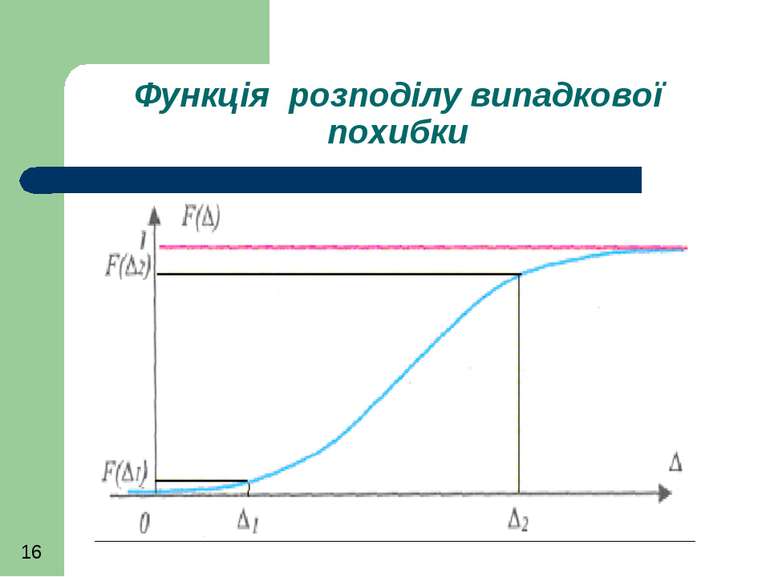
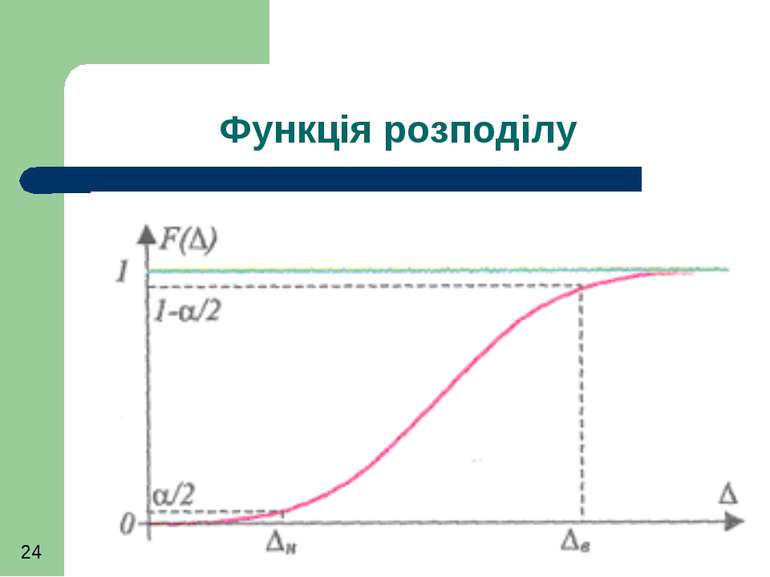
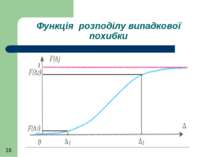
Функція розподілу є інтегральною характеристикою густини розподілу Вона є додатною (як ймовірність), неспадною функцією, що змінює своє значення від 0 до 1.

Функція розподілу випадкової похибки

Знаючи функцію розподілу можна відразу, оминаючи густину розподілу, знайти ймовірність появи похибки в інтервалі

Знаючи функцію розподілу випадкової похибки, диференціюючи її, легко розрахувати густину розподілу

Випадкова похибка може набувати довільні, зокрема теоретично як завгодно великі значення (густина розподілу простягається від - ∞ до +∞). Виключити її неможливо тому, що невідомо яке конкретне значення вона прийме при даному вимірі.

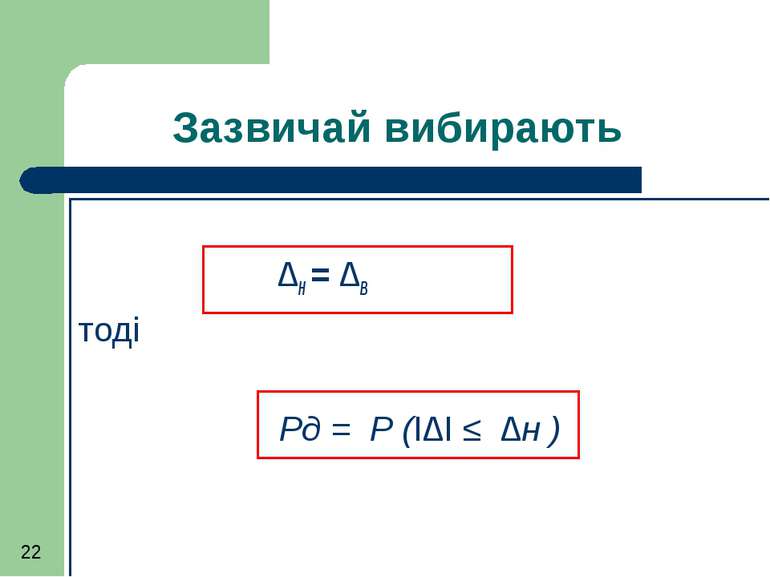
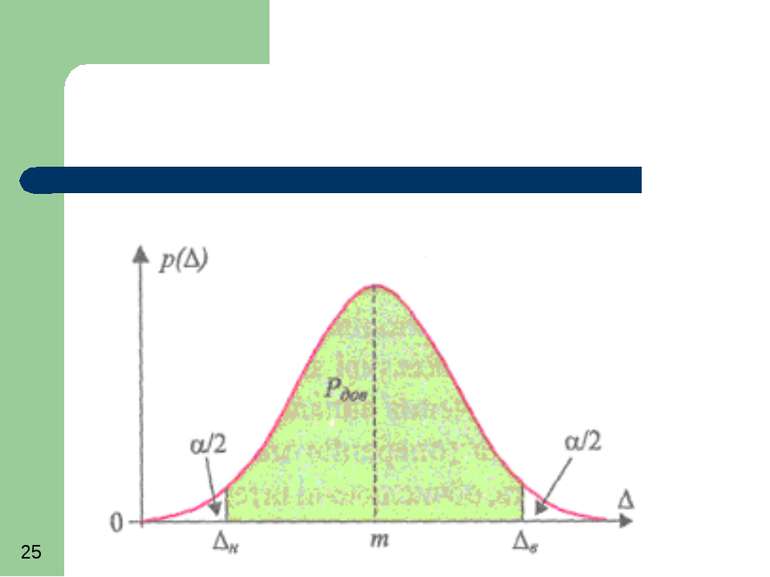
Для оцінювання впливу випадкової похибки на результат виміру задаються діапазоном похибок ∆Н та ∆В (відповідно до очікуваного значення вимірювальної величини Х) та знаходять вірогідність того, що істине значення вимірювальної величини знаходиться між Х-∆Н та Х+∆В

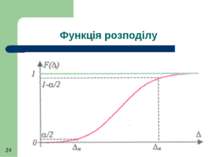
Довірчі границі похибки Інтервал Х-∆Н та Х+∆В називають довірчим інтервалом, а вірогідність того, що Хі знаходиться всередині цього інтервалу довірчою ймовірністю Рд Рд = Р (∆Н≤ ∆ ≤ ∆В )

Зазвичай вибирають ∆Н = ∆В тоді Рд = Р (І∆І ≤ ∆н )

Функція розподілу похибки може бути визначена знизу зверху де α = 1 – Рд - ймовірність (ризик) виходу похибки за межі довірчих границь

Функція розподілу

2.Числові характеристики випадкових похибок

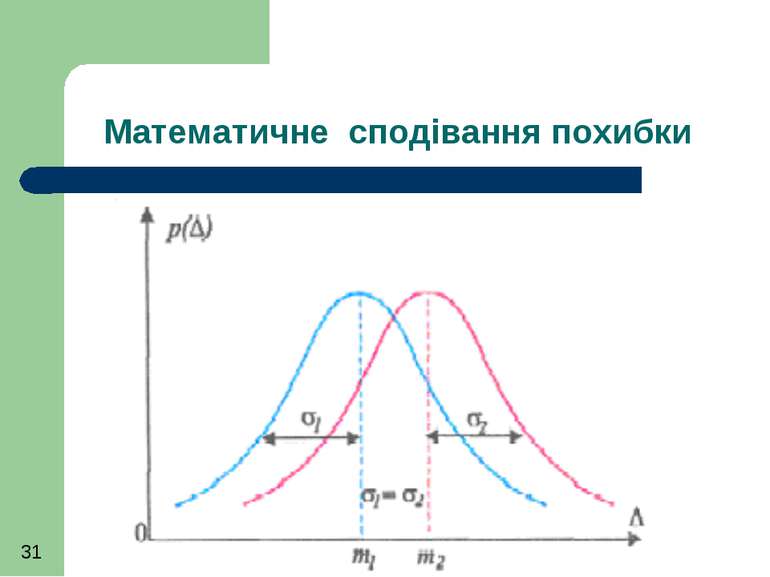
Найуживанішими числовими характеристиками випадкових похибок є математичне сподівання та дисперсія.

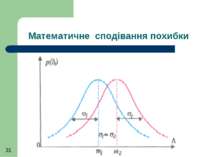
Математичне сподівання m∆ характеризує серединне значення, навколо якого групуються можливі значення похибки. Його практичною оцінкою є середнє значення випадкової похибки.

Під час теоретичного аналізу математичне сподівання М∆ знаходять, обчислюючи інтеграл від добутку похибки на її густину розподілу

Розмірність математичного сподівання дорівнює розмірності похибки.

Математичне сподівання похибки

Дисперсія випадкової похибки міра тісноти групування значень похибки навколо математичного сподівання чи міра розсіювання

Дисперсію знаходять як математичне сподівання квадрата відхилення похибки від її математичного сподівання, тобто обчислюємо інтеграл

Чим більше розсіяння похибки, тим більша її дисперсія Розмірність дисперсії дорівнює квадрату розмірності похибки.

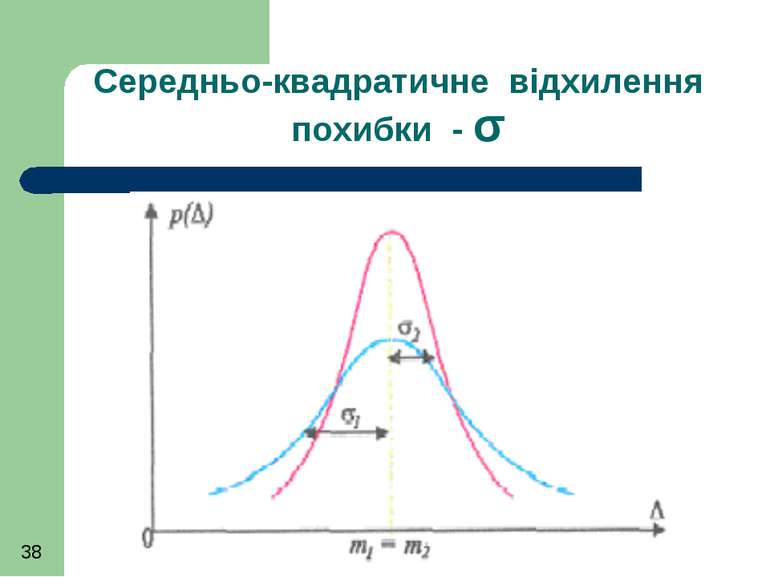
Враховуючи, що розмірність дисперсії дорівнює квадрату розмірності похибки її використання на практиці незручно. Тому замість дисперсії використовують так зване стандартне відхилення, або середнє квадратичне значення похибки (середнє квадратичне відхилення (СКВ) очікуваного результату вимірювання)

Середнє квадратичне відхилення (СКВ) Має ту ж саму розмірність, що і вимірювана величина

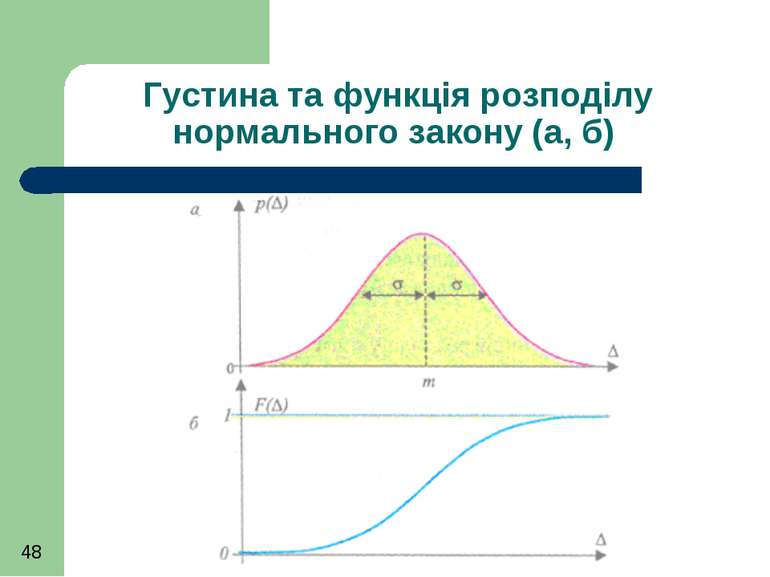
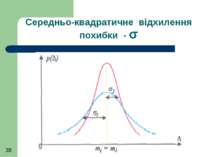
Середнє квадратичне відхилення (СКВ) - σ характеризує ширину розсіянь значень похибки навколо серединного значення m. Зі збільшенням σ густина розподілу стає більш сплющеною до горизонтальної осі (більше розсіяння похибок), а при зменшенні σ вона витягується у вертикальному напрямку (менше розсіяння похибок)

Середньо-квадратичне відхилення похибки - σ

Типові моделі густини розподілу випадкової похибки

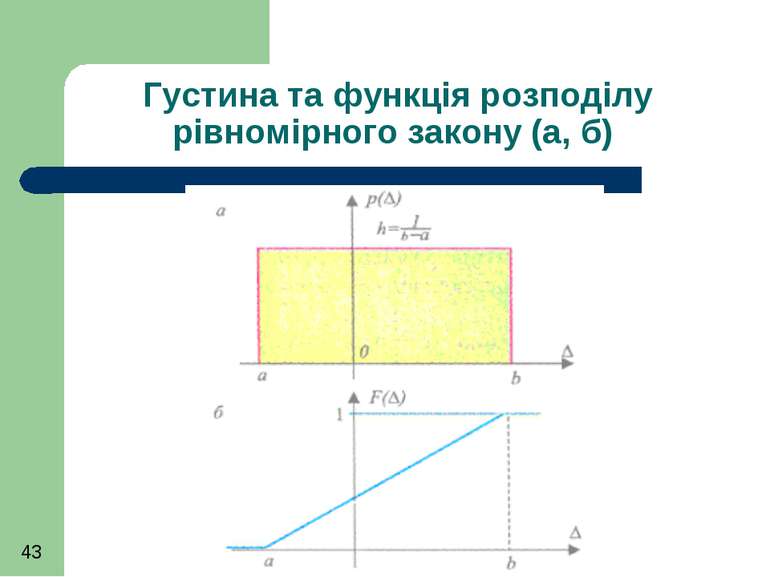
Рівномірний розподіл Характерна однакова частота появи різних похибок в діапазоні від а до b

Для рівномірного розподілу похибки у межах від a до b математичне сподівання можна знайти без обчислення інтеграла як середину прямокутника

Для рівномірного розподілу похибки у межах від a до b дисперсія становить одну дванадцяту від квадрату розмаху

Густина та функція розподілу рівномірного закону (а, б)

Нормальний розподіл Густина нормального (гауссівського) розподілу має дзвоно-подібну форму. За такої форми розподілу при повторних вимірюваннях менші за модулем похибки слід очікувати значно частіше ніж більші, поява додатних та від'ємних похибок рівноможлива.

Особливості нормального закону - алгебраїчна сума довільної кількості випадкових похибок, кожна з яких розподілена за нормальним законом, завжди має нормальний розподіл.

Особливості нормального закону - розподіл алгебраїчної суми великої кількості випадкових похибок з різними розподілами прямує до нормального (так званий закон великої кількості).

Аналітично нормальний розподіл описується виразом де m та σ параметри розподілу.

Густина та функція розподілу нормального закону (а, б)

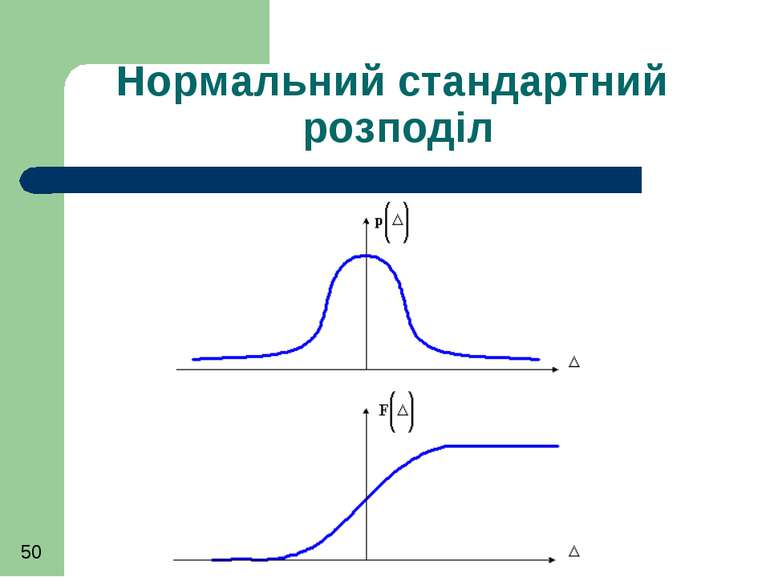
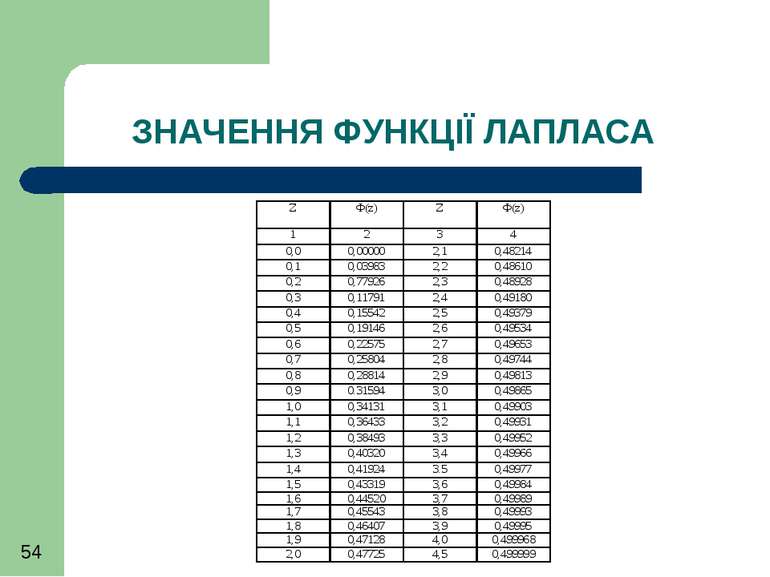
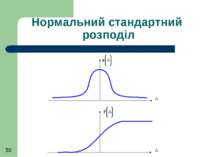
Якщо прийняти m = 0 та σ = 1 то будемо мати так званий стандартний нормальний розподіл, для якого розраховані (затабульовані) таблиці значень густини вірогідності р(Δ) та її функції F (Δ)

Нормальний стандартний розподіл

Для стандартного нормального закону розподілу (при відсутності систематичної складової у сумарній похибці) густина вірогідності р(Δ)

Для стандартного нормального закону розподілу (при відсутності систематичної складової у сумарній похибці) функція розподілу F (Δ)

Де функція Лапласа, що затабульована.

ЗНАЧЕННЯ ФУНКЦІЇ ЛАПЛАСА

При наявності систематичної складової Δс у складі загальної похибки

Оцінку попадання похибки у довірчій інтервал ΔН - ΔВ при наявності систематичної складової ΔС провадять за виразом

Якщо систематична складова відсутня, то маємо вираз

Ця модель може бути використана при використанні при обчисленні середнього значення вимірюваваного параметра за результатами більш, ніж 20 спостережень.

При малому числі спостережень (n

Коефіцієнт Стьюдента

Показником точності є інтервал, у якому із установленою ймовірністю P знаходять сумарну похибку виміру: Х; (x) від Н(х) до В(х); P, де: (x), Н(х), В(х) - похибка виміру відповідно з нижньою й верхньою границею, у тих же одиницях; Р імовірність, з якої похибка виміру перебуває в цих границях.

Наприклад: 121 м/с; від -1 до 2 м/с; Р = 0,99.

При симетричному довірчому інтервалі допускається записувати результат у вигляді (Х ); Р. Наприклад: (100±1) В; Р=0,95,

При запису результату необхідно дотримувати наступні правила: число значущих цифр у показнику точності повинне бути не більше двох; останній розряд середнього визначається останнім розрядом похибки.

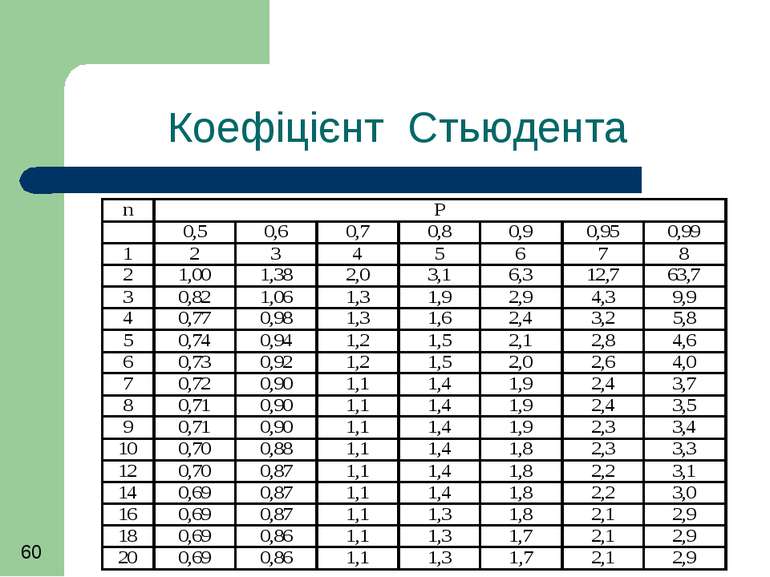
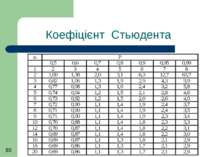
Обчислення показників точності виконують у такому порядку: 1/ обчислюють середнє арифметичне серії вимірів X ; 2/ знаходять оцінку СКВ результату x, 3/ задавшись імовірністю P по таблиці знаходять t із графи, що відповідає даному P і числу спостережень n; 4/ знайдений довірчий інтервал представляють у вигляді t x

Пример обработки ряда прямых измерений

При измерении напряжения источника питания получены следующие результаты, В: 9,78; 9,65; 9,83; 9,69; 9,74; 9,80; 9,68: 9,71; 9,81.

1. Находят среднее арифметическое и принимают его за результат измерения:

2. Определяют СКО погрешности результата измерения:

3. Определяют доверительный интервал погрешности измерения Поскольку в рассматриваемой задаче число измерений n

4. Записывают результат измерения согласно первой формеГОСТ 8.011-72: 9,74 В; Δ от -0,05 до 0,05 В; Р = 0,95.