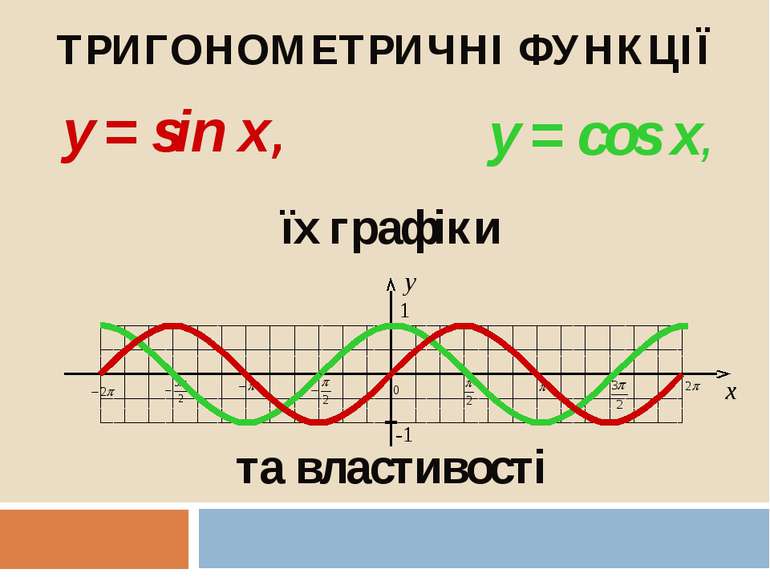
Презентація на тему:
"Властивості та графіки функцій y=sin x та y=cos x"

Презентація на тему: “Властивості та графіки функцій y=sin x та y=cos x”

ТРИГОНОМЕТРИЧНІ ФУНКЦІЇ y = sin x, y = cos x, їх графіки та властивості y 1 -1 x

Синус (від лат. sinus) – вигин, кривизна

Побудова графіка функції y = sin x

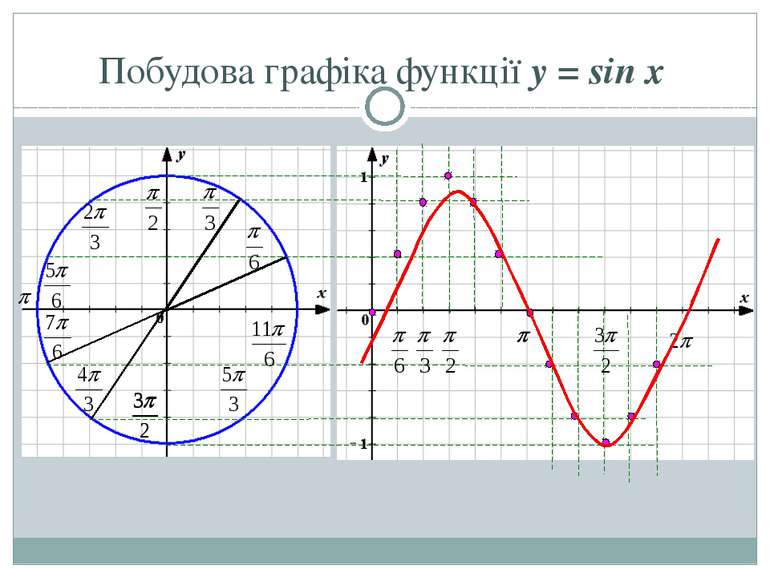
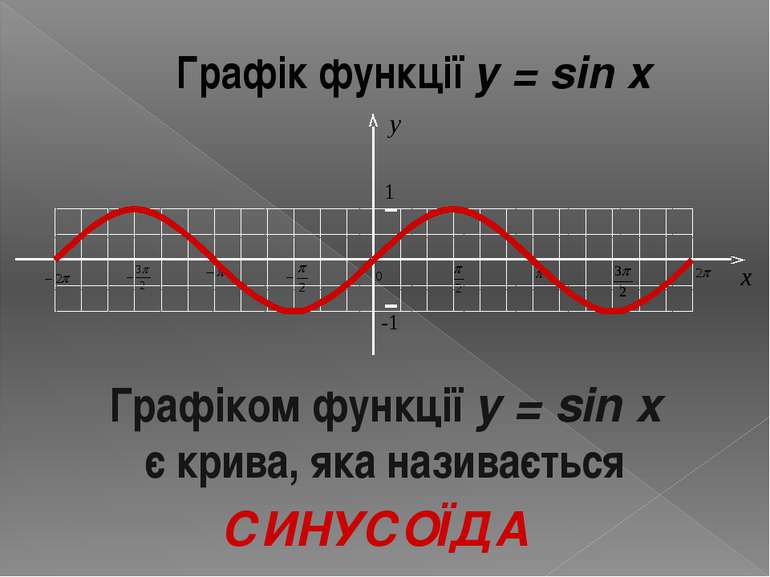
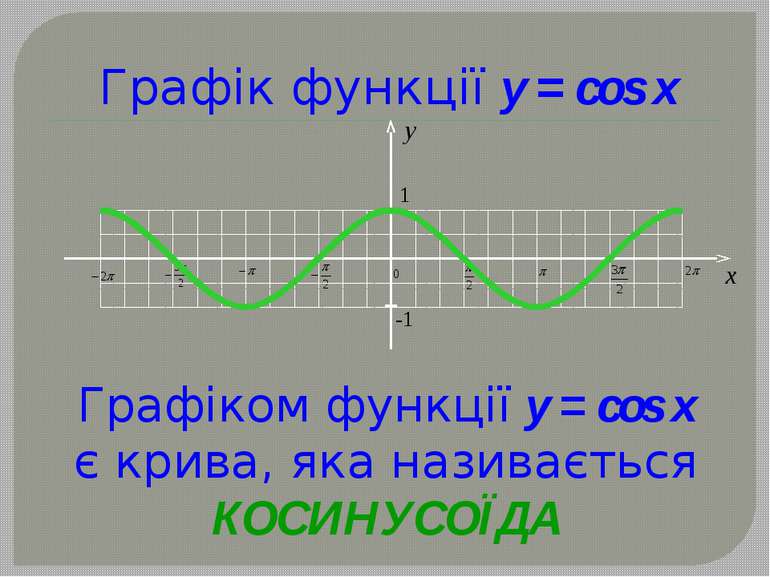
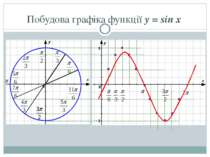
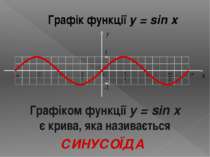
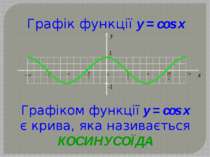
Графік функції y = sin x Графіком функції y = sin x є крива, яка називається СИНУСОЇДА y 1 -1 x

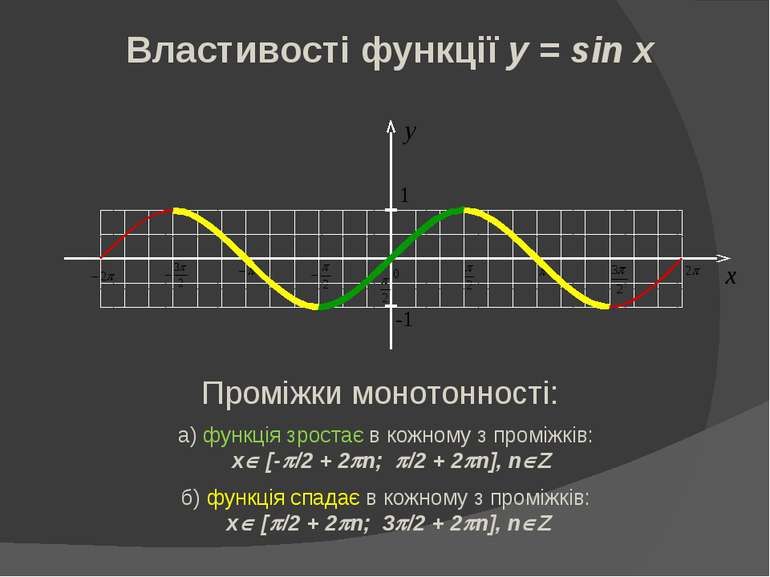
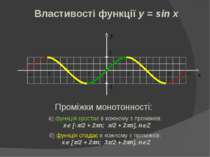
Властивості функції y = sin x Проміжки монотонності: а) функція зростає в кожному з проміжків: xÎ [-p/2 + 2pn; p/2 + 2pn], nÎZ б) функція спадає в кожному з проміжків: xÎ [p/2 + 2pn; 3p/2 + 2pn], nÎZ y 1 -1 x

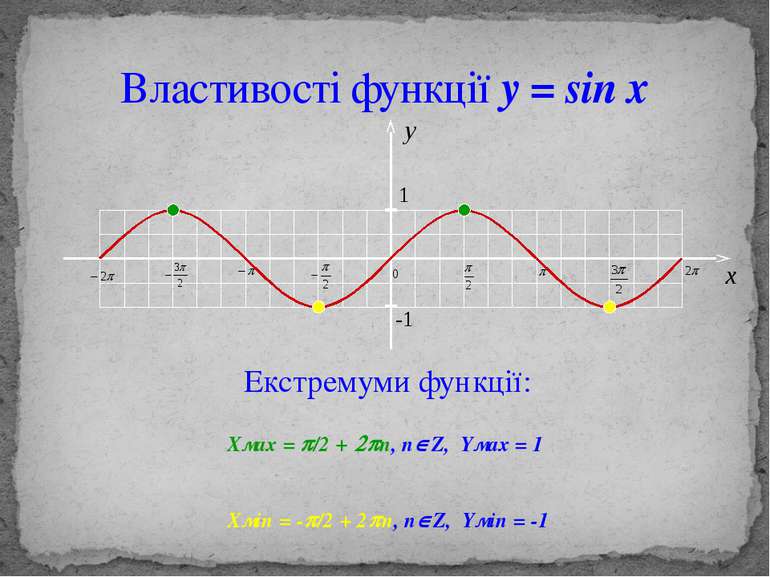
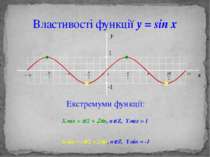
Властивості функції y = sin x Екстремуми функції: Хмах = p/2 + 2pn, nÎZ, Yмах = 1 Хмin = -p/2 + 2pn, nÎZ, Yмin = -1 y 1 -1 x

Графік функції y = cos x Графіком функції y = cos x є крива, яка називається КОСИНУСОЇДА

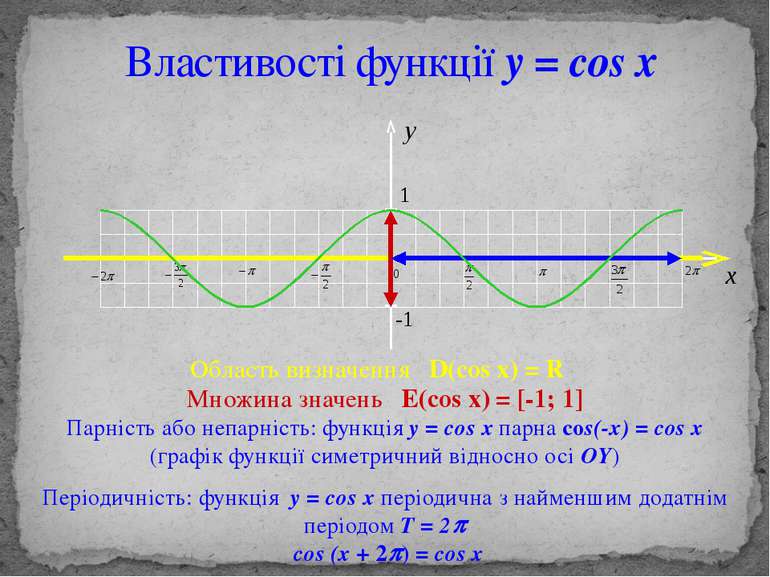
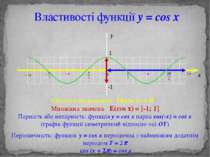
Властивості функції y = cos x Область визначення D(cos x) = R Множина значень E(cos x) = [-1; 1] Парність або непарність: функція y = cos x парна cos(-x) = cos x (графік функції симетричний відносно осі OY) Періодичність: функція y = cos x періодична з найменшим додатнім періодом T = 2p cos (x + 2p) = cos x y 1 -1 x

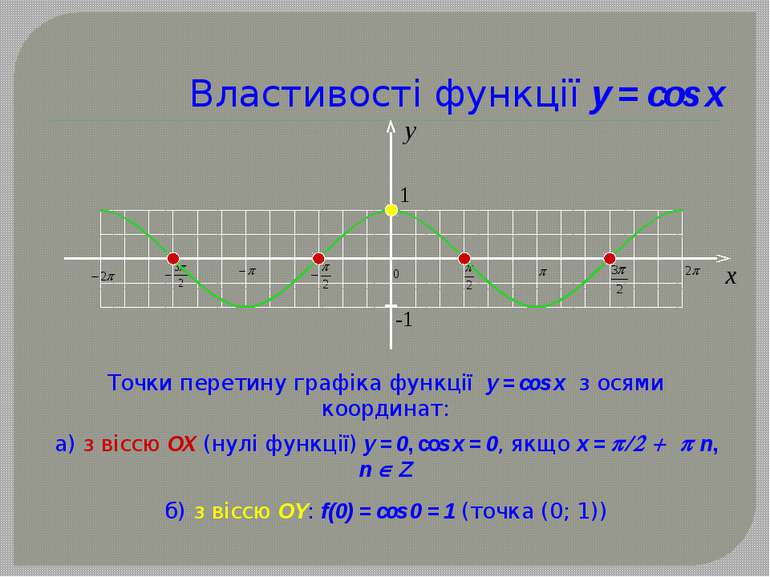
Точки перетину графіка функції y = cos x з осями координат: Властивості функції y = cos x а) з віссю ОХ (нулі функції) у = 0, cos x = 0, якщо х = p/2 + p n, n Î Z б) з віссю ОY: f(0) = cos 0 = 1 (точка (0; 1)) y 1 -1 x

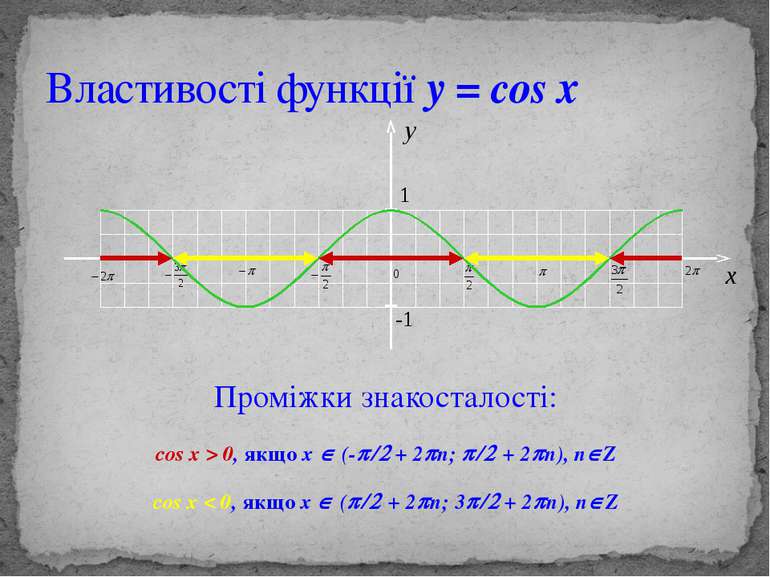
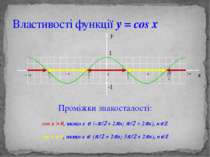
Властивості функції y = cos x Проміжки знакосталості: cos x > 0, якщо х Î (-p/2 + 2pn; p/2 + 2pn), nÎZ cos x < 0, якщо x Î (p/2 + 2pn; 3p/2 + 2pn), nÎZ y 1 -1 x

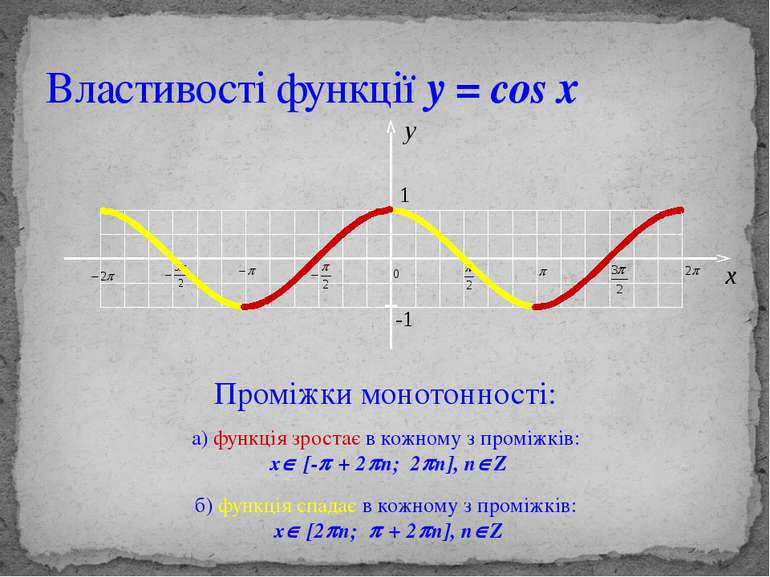
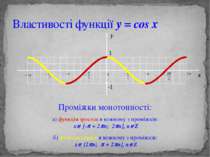
Властивості функції y = cos x Проміжки монотонності: б) функція спадає в кожному з проміжків: xÎ [2pn; p + 2pn], nÎZ а) функція зростає в кожному з проміжків: xÎ [-p + 2pn; 2pn], nÎZ y 1 -1 x

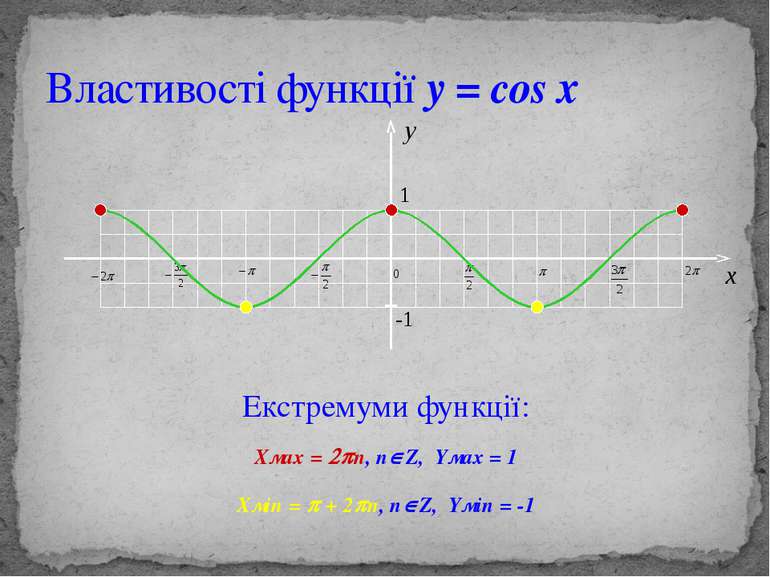
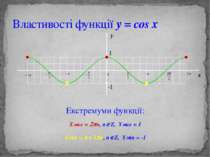
Властивості функції y = cos x Екстремуми функції: Хмах = 2pn, nÎZ, Yмах = 1 Хмin = p + 2pn, nÎZ, Yмin = -1 y 1 -1 x

Дякую за увагу!