Презентація на тему:
Трапеція. Теорема Фалеса

Навчальна презентація до уроку 18 “Теорема Фалеса” Тема1.2. Трапеція. Теорема Фалеса

Актуалізація опорних знань учнів Питання класу Який чотирикутник називається паралелограмом? Які властивості мають сторони паралелограма? Сформулюйте ознаки рівності трикутників. Як за допомогою циркуля та лінійки розділити відрізок на дві рівні частини? на три рівні частини?

Теорема Фалеса

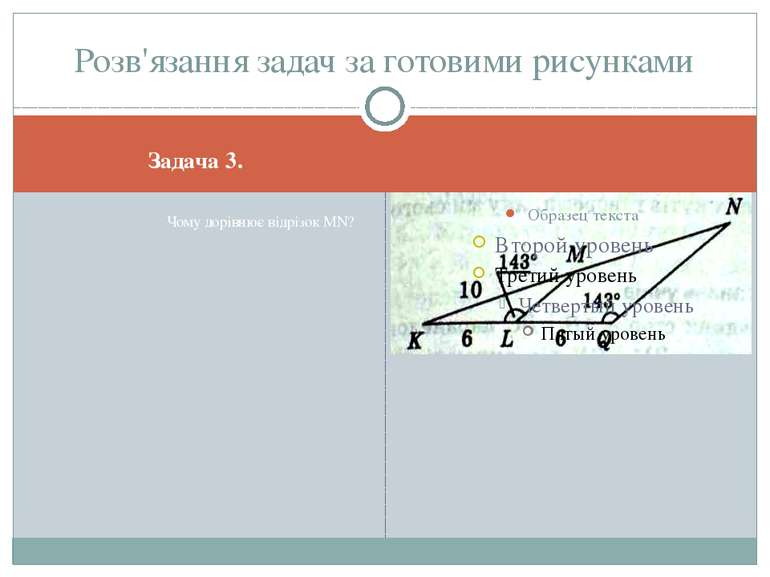
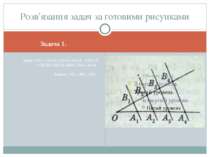
Задача 1. Дано: ОА1 = А1А2=А2А3=А3А4, А1В1 ∥ А2В2∥ А3В3 ∥ А4В4, ОВ4 = 8 см. Знайти: ОВ1, ОВ2, ОВ3. Розв'язання задач за готовими рисунками

Задача 2. Чому дорівнює відрізок АС? Розв'язання задач за готовими рисунками

Задача 3. Чому дорівнює відрізок MN? Розв'язання задач за готовими рисунками

Задача 4. Чому дорівнює відрізок CD? Розв'язання задач за готовими рисунками

Алгоритм розділення відрізка на n рівних частин 1). Провести з одного кінця А відрізка АВ півпряму, яка не лежить на прямій, що містить відрізок АВ. 2). На півпрямій від початку А відкласти рівні відрізки (необхідна кількість n). 3). Кінець останнього відрізка на півпрямій Аn сполучити з другим кінцем В цього відрізка АВ. 4). Провести через кінці А n-1, А n-2 ,... А, відрізків, відкладених на півпрямій, прямі, паралельні АnВ. 5). Вони перетнуть цей відрізок АВ у точках В n -1, В n-2, В n-3, ... В1, які ділять відрізок АВ на n рівних частин (за теоремою Фалеса).

У середині VII ст. до н. е. західне узбережжя Малої Азії належало Греції. Середня частина цього узбережжя називалася Іонією. В Іонії були великі міста, що вели торгівлю з багатьма країнами. В одному з цих, у Мілеті, жив Фалес (близько 640—548 pp. до н. в.), якого вважають родоначальником грецької математики. Торговельні спра ви привели Фалеса до Єгипту, де він познайомився з єгипетською наукою. Геометрія зацікавила Фалеса найбільше. Решту життя вій присвятив не лише засвоєнню створеного єгиптянами в галузі геометрії, але і її розробці. Вважають, що Фалесу належить перше доведення теореми про рівність кутів при основі рівнобедреного трикутника, рівность вертикальних кутів і теореми, яку ми сьогодні довели. Історична довідка про Фалеса Мілетського

Фалес Мілетський Фалес Мілетський мав титул одного із семи мудреців Греції, він насправді був першим філософом, першим математиком, астрономом й, взагалі, першим по всіх науках у Греції. Він був те ж для Греції, що Ломоносов для Росії. Фалесу Мілетському приписують простий спосіб визначення висоти піраміди. У сонячний день він поставив свій посох там, де кінчалася тінь від піраміди. Потім він показав, що як довжина однієї тіні відноситься до довжини іншої тіні, так і висота піраміди відноситься до висоти посоха.

Біографія Походив із знатного фінікійського роду. У своїй творчості поєднував питання практики з теоретичними проблемами, що стосувались проблем Всесвіту. Він багато подорожував, зокрема, у молодості відвідав Єгипет, де в школах Мемфіса і Фів вивчав різні науки. Повернувшись на батьківщину, заснував у Мілеті філософську школу. Усі натурфілософські пізнання Фалес використовував для створення завершеного філософського вчення. Так, він вважав, що все існуюче породжене водою. Вода — це джерело, з якого все постійно виникає. При цьому вода й усе, що з неї виникло, не є мертвими, вони живі. Як приклад, Фалес згадував магніт і янтар: вони породжують рух, отже, вони мають душу. Фалес уявляв увесь світ пронизаним життям. Він заклав теоретичні основи вчення, що має назву гілозоїзм. Хоча гілозоїзм має свої корені в міфології, у Фалеса він одержує філософське обґрунтування. Фалес Мілетський

Наукова спадщина Фалеса вважають першим грецьким астрономом. Він передбачив сонячне затемнення (28 травня 585 до н. е.). Йому належить заслуга у визначенні часу сонцестояння і рівнодення, у встановленні тривалості року в 365 днів, відкриття факту руху Сонця відносно зірок. У наш час іменем Фалеса названо кратер на видимій стороні Місяця. Фалес також має великі заслуги у створенні наукової математики. У нього вперше в історії математики зустрічаються доведення теорем. Якщо єгипетських землемірів задовольняла відповідь на питання «Як?», то Фалес, мабуть, першим у світі поставив питання «Чому?» й успішно відповів на нього. Нині відомо, що багато математичних правил були відкриті набагато раніше, ніж у Стародавній Греції. Але усі — дослідним шляхом. Строго логічне доведення правильності тверджень на підставі загальних положень, прийнятих за достовірні істини, було винайдено греками. Характерна і зовсім нова риса грецької математики полягає в поступовому переході за допомогою доведення від одного твердження до іншого. Саме такий характер математиці був наданий Фалесом. І навіть сьогодні, розпочинаючи доведення, наприклад, теореми про властивості ромба, ми, по суті, міркуємо майже так само, як це робили учні Фалеса. Вважається, що Фалес першим познайомив греків з геометрією. Йому приписують відкриття і доведення ряду теорем: про поділ кола діаметром навпіл; про те, що кут, вписаний у півколо, є прямим (Теорема Фалеса); про рівність кутів при основі рівнобедреного трикутника; про рівність вертикальних кутів; про пропорційність відрізків, утворених на прямих, що перетинаються декількома паралельними прямими (Теорема Фалеса (пропорційні відрізки)). Фалес установив, що трикутник повністю визначається стороною і прилеглими до неї кутами. Фалес відкрив цікавий спосіб визначення відстані від берега до видимого корабля. Деякі історики стверджують, що для цього він використав ознаку подібності прямокутних трикутників. Фалесу приписують також спосіб визначення висоти різних предметів, зокрема пірамід, за довжиною тіні, коли сонце піднімається над горизонтом на 45 градусів. В «Політиці» Аристотеля знаходиться фрагментарний уривок про те, як Фалес за допомогою астрономічних знань зміг передбачити врожай олив та використати цей факт в цілях власного збагачення, показавши, що філософи здатні стати багатими, хоча цього й першочергово не прагнуть. За те, що він зрозумів вплив дефіциту товарів на процес ціноутворення, його можна вважати також раннім економістом. Усі ці досягнення принесли Фалесу славу першого мудреця серед знаменитих «семи мудреців» далекого минулого. Якщо паралельні прямі, що перетинають дві задані прямі а і b, відтинають на одній прямій рівні відрізки, то вони відтинають рівні відрізки і на другій прямій:

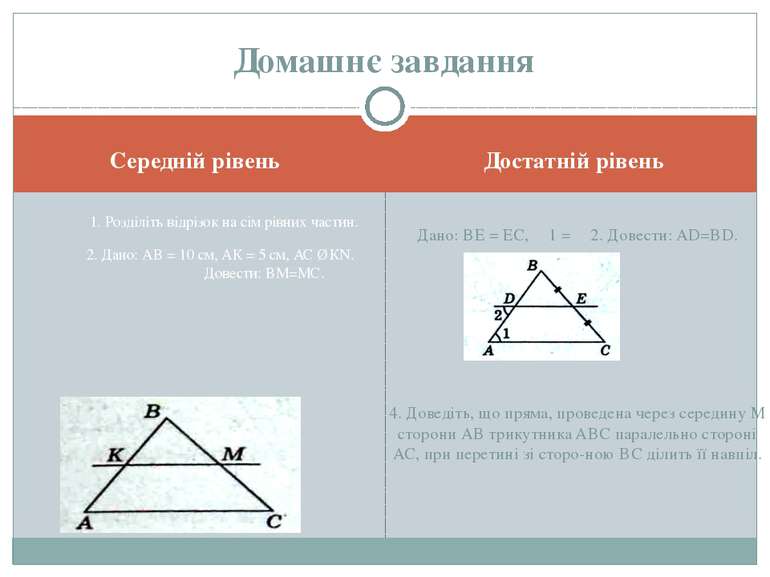
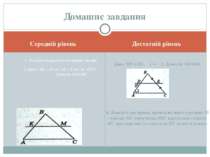
Середній рівень Достатній рівень 1. Розділіть відрізок на сім рівних частин. 2. Дано: АВ = 10 см, АК = 5 см, АС ∥ КN. Довести: ВМ=МС. Дано: ВЕ = ЕС, ∠1 = ∠2. Довести: AD=BD. 4. Доведіть, що пряма, проведена через середину М сторони АВ трикутника ABC паралельно стороні АС, при перетині зі сторо ною ВС ділить її навпіл. Домашнє завдання

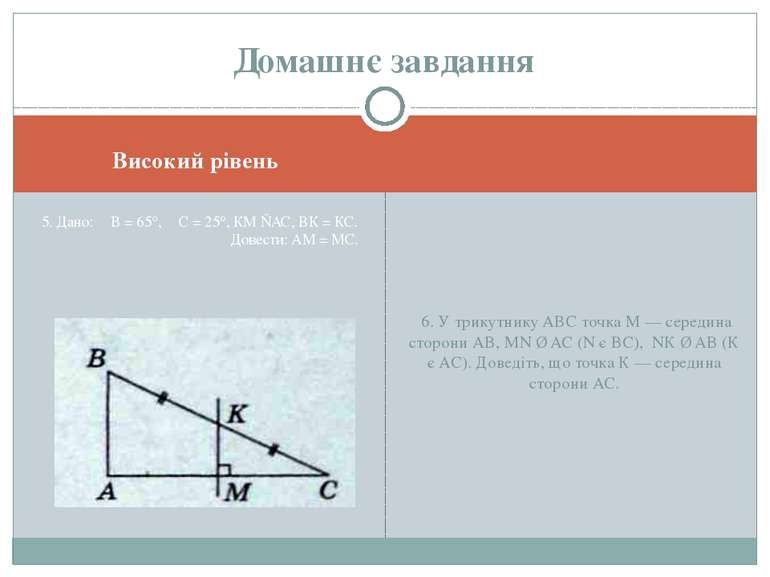
Високий рівень 5. Дано: ∠B = 65°, ∠C = 25°, КМ ⊥АС, ВК = КС. Довести: AM = МС. 6. У трикутнику ABC точка М — середина сторони АВ, MN ∥ АС (N є ВС), NК ∥ АВ (К є АС). Доведіть, що точка К — середина сторони АС. Домашнє завдання