Презентація на тему:
Теорема Піфагора

Пам 'ятка для учня Будь уважним. Активно пізнавай та аналізуй нове. Самостійно встановлюй зв'язки відомого з невідомим. Учись відчувати радість відкриття.

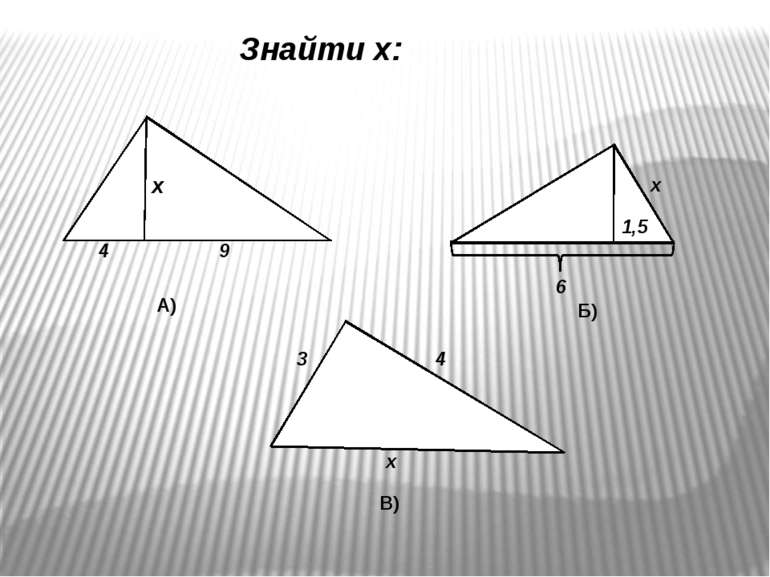
Який трикутник називається прямокутним? Як називаються сторони прямокутного трикутника? Сформулювати властивість катета, що лежить проти кута в 300. Чому дорівнюють кути рівнобедреного прямокутного трикутника?

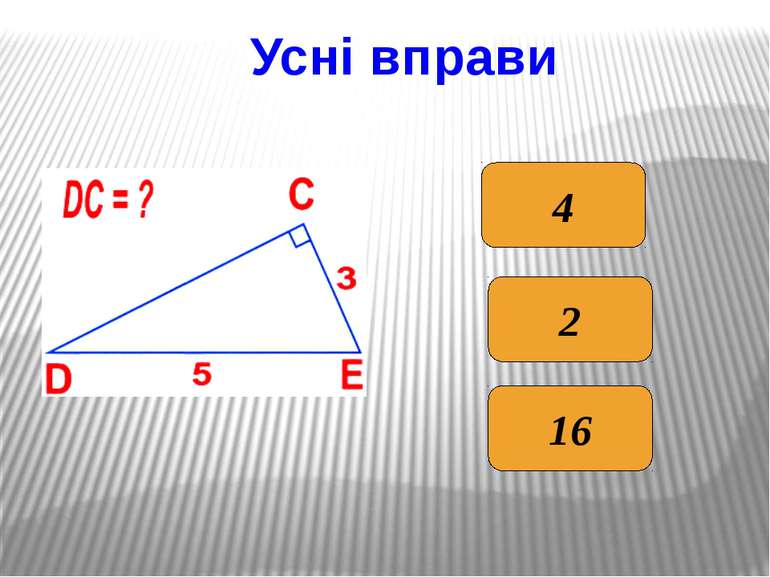
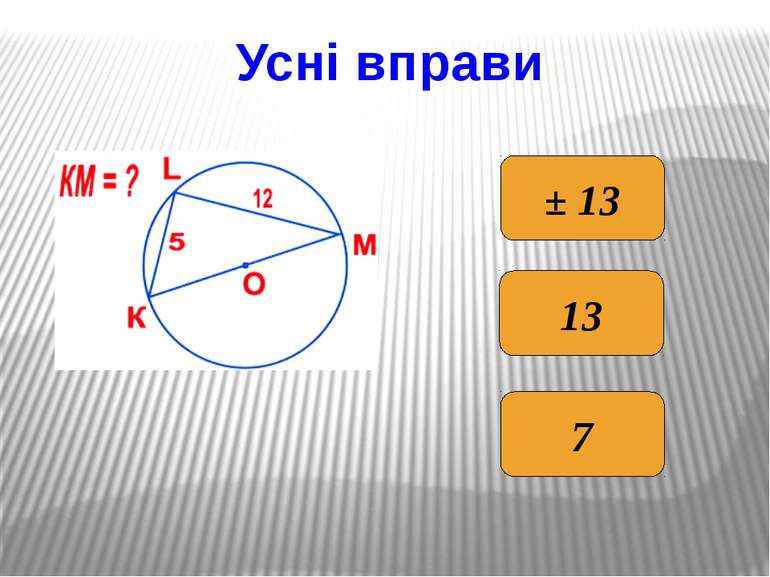
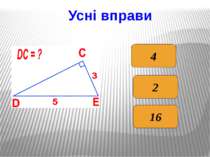
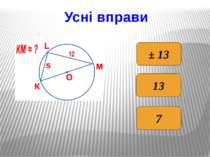
Метричні співвідношення в прямокутному трикутнику у прямокутному трикутнику висота, проведена до гіпотенузи, є середнім пропорційним …; у прямокутному трикутнику катет є середнім пропорційним …; висота, проведена до гіпотенузи, дорівнює добутку … . Продовжити речення:

х 4 9 х 1,5 6 А) Б) 3 4 х В) Знайти х:

Очікувані результати після уроку знатимемо: теорему Піфагора; ознаку прямокутного трикутника умітимемо: доводити теорему Піфагора; застосовувати теорему Піфагора під час розв'язування задач; знаходити гіпотенузу та катети прямокутного трикутника зможемо: розвивати навички проведення власних спостережень, увагу, пам’ять, логічне мислення, розумові творчі здібності, самостійні пошукові творчі дії. Теорема Піфагора

Піфагор жив у VI ст. до н.е. в Давній Греції. Він народився близько 580 р. до н.е.на острові Самос. Батьком Піфагора був Мнесарх, різьбяр по коштовних каменях. Ім'я матері Піфагора невідоме.

Піфагор багато подорожував, його ім'я було оточене багатьма легендами, тому тепер важко визначити, що зробив він сам, а що запозичив у інших. Залежність між сторонами прямокутного трикутника була відома ще за 1000 років до Піфагора в Давніх Вавилоні та Єгипті. Піфагору, оче видно, належить доведення цієї теореми і широке застосування її під час розв'язування задач.

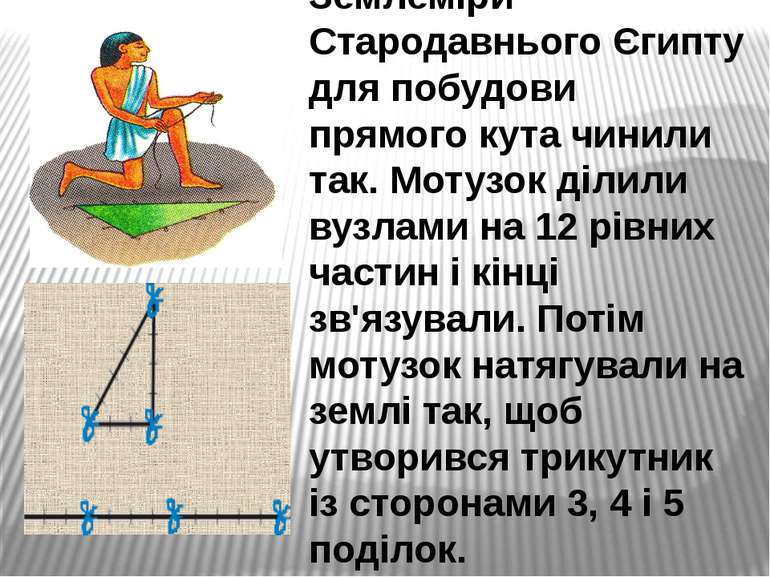
Землеміри Стародавнього Єгипту для побудови прямого кута чинили так. Мотузок ділили вузлами на 12 рівних частин і кінці зв'язували. Потім мотузок натягували на землі так, щоб утворився трикутник із сторонами 3, 4 і 5 поділок.

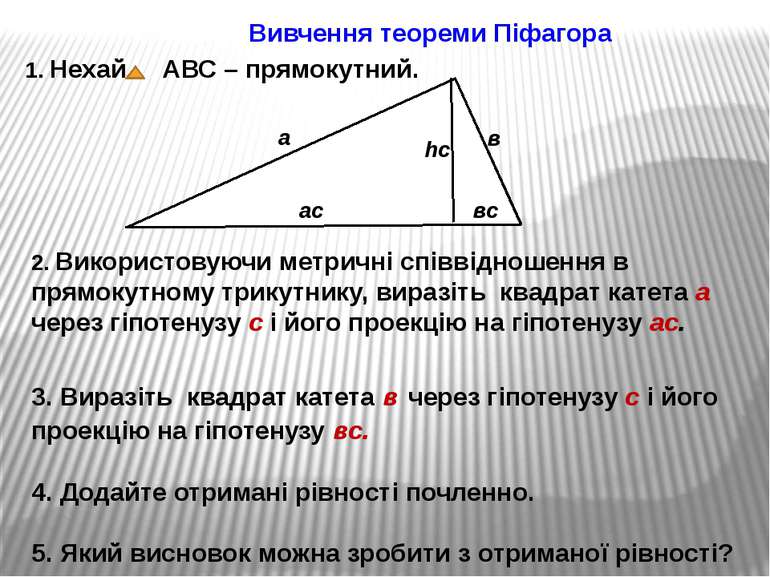
Вивчення теореми Піфагора 1. Нехай АВС – прямокутний. 2. Використовуючи метричні співвідношення в прямокутному трикутнику, виразіть квадрат катета а через гіпотенузу с і його проекцію на гіпотенузу ас. 3. Виразіть квадрат катета в через гіпотенузу с і його проекцію на гіпотенузу вс.   4. Додайте отримані рівності почленно. 5. Який висновок можна зробити з отриманої рівності? в вс ас hс а

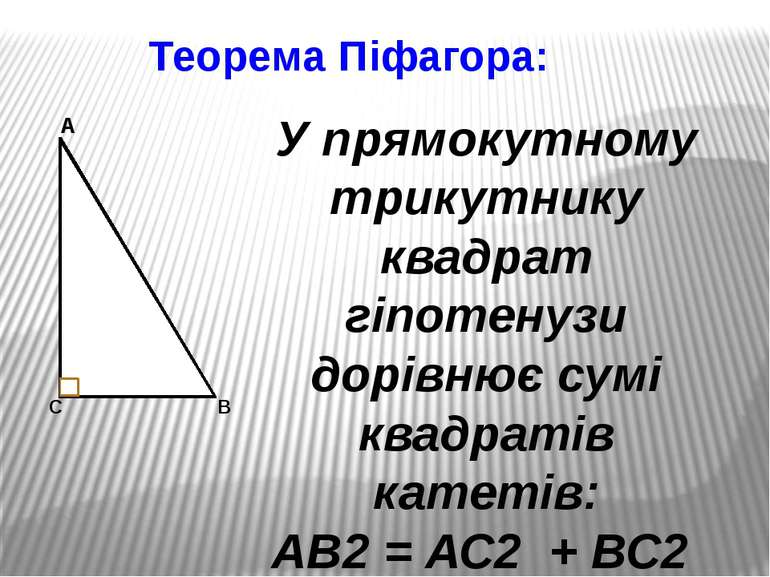
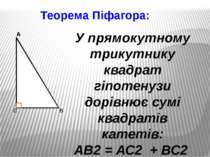
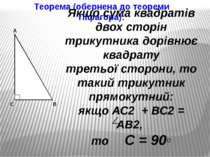
Теорема Піфагора: У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів: АВ2 = АС2 + ВС2 А В С

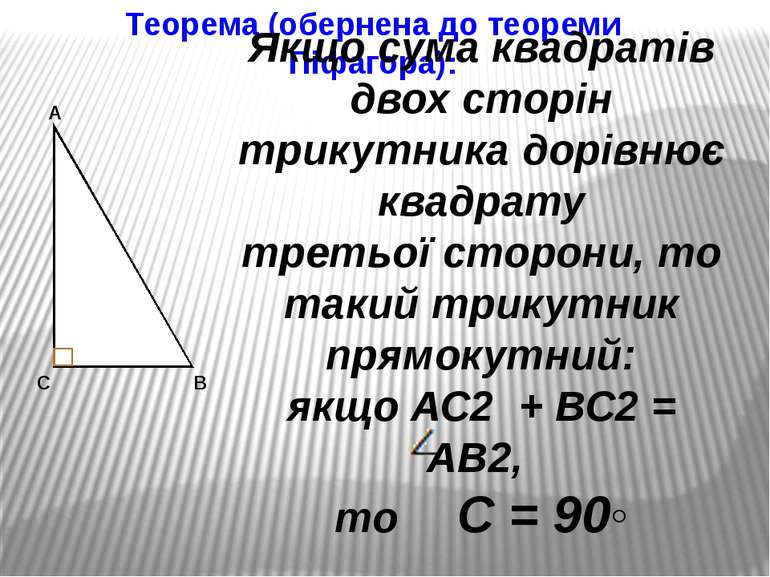
Теорема (обернена до теореми Піфагора): Якщо сума квадратів двох сторін трикутника дорівнює квадрату третьої сторони, то такий трикутник прямокутний: якщо АС2 + ВС2 = АВ2, то С = 90◦ А В С

Теорема Піфагора чудова тим, що вона зовсім не очевидна. Із простого споглядання прямокутного трикутника не зробиш висновок, що між його сторонами є таке просте співвідношення: с2=а2+Ь2. Але це співвідношення стає очевидним, якщо вдало побудувати малюнок. У математичних трактатах давньої Індії часто наводили тільки рисунок, супроводжуючи його лише одним словом: «Дивись!»

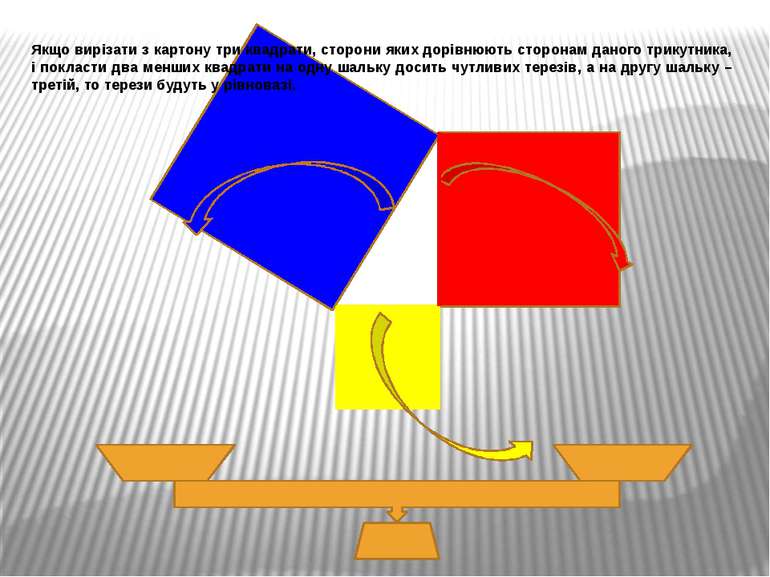
Якщо вирізати з картону три квадрати, сторони яких дорівнюють сторонам даного трикутника, і покласти два менших квадрати на одну шальку досить чутливих терезів, а на другу шальку – третій, то терези будуть у рівновазі.

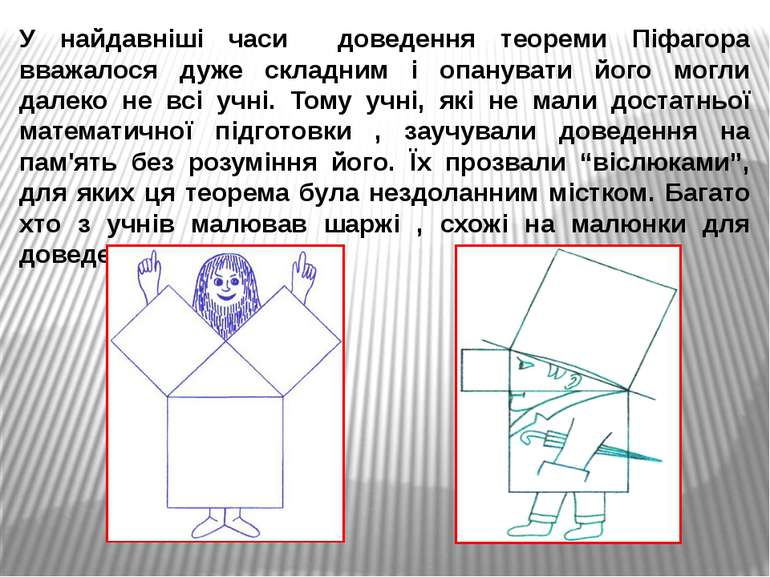
У найдавніші часи доведення теореми Піфагора вважалося дуже складним і опанувати його могли далеко не всі учні. Тому учні, які не мали достатньої математичної підготовки , заучували доведення на пам'ять без розуміння його. Їх прозвали “віслюками”, для яких ця теорема була нездоланним містком. Багато хто з учнів малював шаржі , схожі на малюнки для доведення теореми.

1) Чи можуть сторони прямокутного трикутника дорівнювати 5, 6, 7 см? А. Так. Б. Ні. 2) Катети прямокутного трикутника дорівнюють 5 і 12 см. Чому дорівнює гіпотенуза трикутника? А. 15 см. Б. 14 см. В. 13 см. Г. 16 см. 3) Гіпотенуза прямокутного трикутника дорівнює 10 см, а один з катетів 8 см. Чому дорівнює другий катет? А. 25 см. Б. 6 см. В. 5 см. Г. 1 см.

Усні вправи 4 2 16

Усні вправи 13 7 ± 13

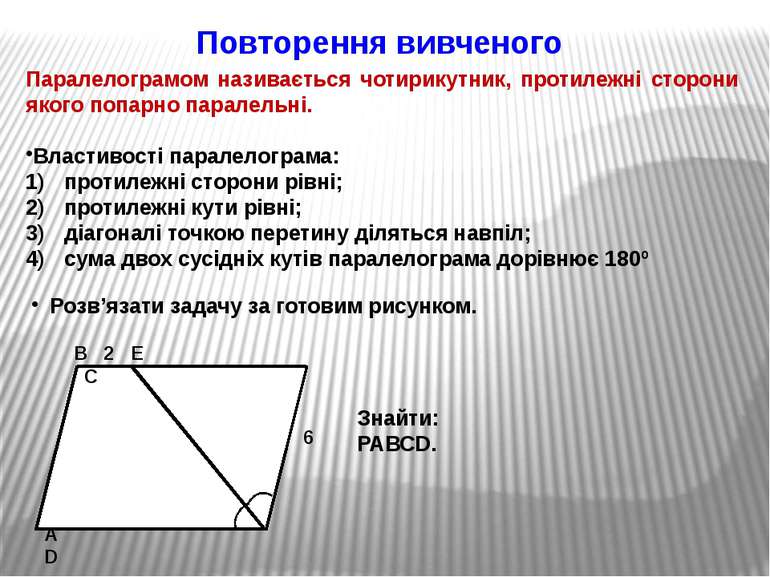
Повторення вивченого Паралелограмом називається чотирикутник, протилежні сторони якого попарно паралельні. Властивості паралелограма: протилежні сторони рівні; протилежні кути рівні; діагоналі точкою перетину діляться навпіл; сума двох сусідніх кутів паралелограма дорівнює 180º В 2 Е С А D 6 Знайти: РАВСD. Розв’язати задачу за готовим рисунком.

Так сказав Піфагор 1. Живи з людьми так, щоб твої друзі не стали недругами, а недруги стали друзями. 2. Твори велике, не обіцяючи великого. 3. Не заплющуй очей, коли хочеш спати, не проаналізувавши всіх своїх учинків за минулий день. 4. Тимчасова невдача краще тимчасової удачі. 5. Не роби нічого ганебного ні в присутності інших, ні таємно. Першим твоїм законом має бути повага до себе самого. 6. Лише неблагородна людина здатна в очі хвалити, а поза очі злословити. 7. Роби лиш те, що в майбутньому не засмутить тебе. 8.Усе впорядковується відповідно до чисел.