Презентація на тему:
Теорема Піфагора. Варіант 4

Презентацiя На тему: Теорема Пiфагора

Пiфагор Піфагор Самоський (др.-греч Πυθαγόρας ὁ Σάμιος, лат Піфагора ..... 570-490рр. до н е.) - старогрецький філософ, математик і містик, творець релігійно-філософської школи піфагорійців. Історію життя Піфагора важко відокрем-ити від легенд, що представляють його як досконалого мудреця і великого присвяченого в усі таїнства греків і варварів. Ще Геродот називав його «найб-ільшим еллінським мудрецем» Таким чином, найбільш ранні відомі джерела про вчення Піфагора з'явилисялише 200 років після його смерті. Сам Піфагор не залишив творів, і всі відомості про нього і його вченні грунтуються на працях його послідовників, не завжди неупереджених. На честь Піфагора названий кратер на Місяці.

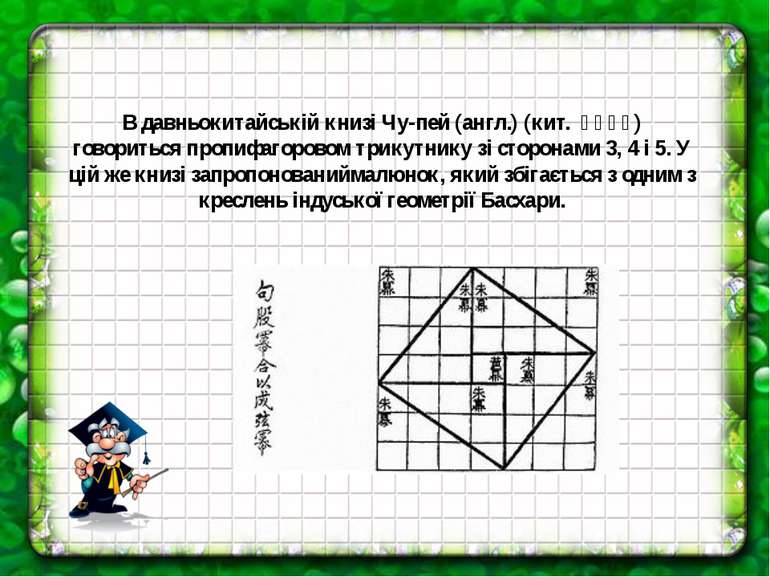
В давньокитайській книзі Чу-пей (англ.) (кит. 周 髀 算 经) говориться пропифагоровом трикутнику зі сторонами 3, 4 і 5. У цій же книзі запропонованиймалюнок, який збігається з одним з креслень індуської геометрії Басхари.

Моріц Кантор (найбільший німецький історик математики) вважає, що рівність3 ² + 4 ² = 5 ² було відомо вже єгиптянам ще Близько 2300 р. до н. е.., за часівцаря Аменемхета I (згідно папірусу 6619 Берлінського музею). На думкуКантора, гарпедонапти, або «натягівателі мотузок», будували прямі кути за допомогою прямокутних трикутників зі сторонами 3, 4 і 5.

Дуже легко можна відтворити їхній спосіб побудови. Візьмемо мотузкудовжиною в 12 м і прив'яжемо до неї по кольоровий смужці на відстані 3 м відодного кінця і 4 метра від іншого. Прямий кут виявиться укладеним міжсторонами довжиною в 3 і 4 метри.

Приблизно в 400 р. до н. е.., згідно Проклу, Платон дав метод знаходження піфагорових трійок, що поєднує алгебру і геометрію. Приблизно в 300 р. до н.е.. в «Засадах» Евкліда з'явилося найстаріше аксіоматичне доведення теореми Піфагора. Дещо більше відомо про теорему Піфагора у вавилонян. В одному вiдносно до часу Хаммурапі, тобто до 2000 року до н. Е.., Наводиться наближене обчислення гіпотенузи прямокутного трикутника. Звідси можна зробити висновок, що в Дворіччі вміли робити обчислення з прямокутними трикутниками, принаймні в деяких випадках.

Формулювання Геометрична формулювання: Спочатку теорема була сформульована таким чином: У прямокутному трикутнику площа квадрата, побудованого на гіпотенузі, дорівнює сумі площ квадратів, побудованих на катетах. Алгебричне  формулювання: У прямокутному трикутнику квадрат довжини гіпотенузи дорівнює сумі квадратів довжин катетів.

Тобто, позначивши довжину гіпотенузи трикутника через c, а довжини катетів через  а i b Обидві формулювання теореми еквівален-тні, але друга формулювання більш елементарна, вона не вимагає поняття площі. Тобто друге твердження можна перевірити, нічого не знаючи про площу і вимірявши тільки довжини сторін прямокутного трикутника.

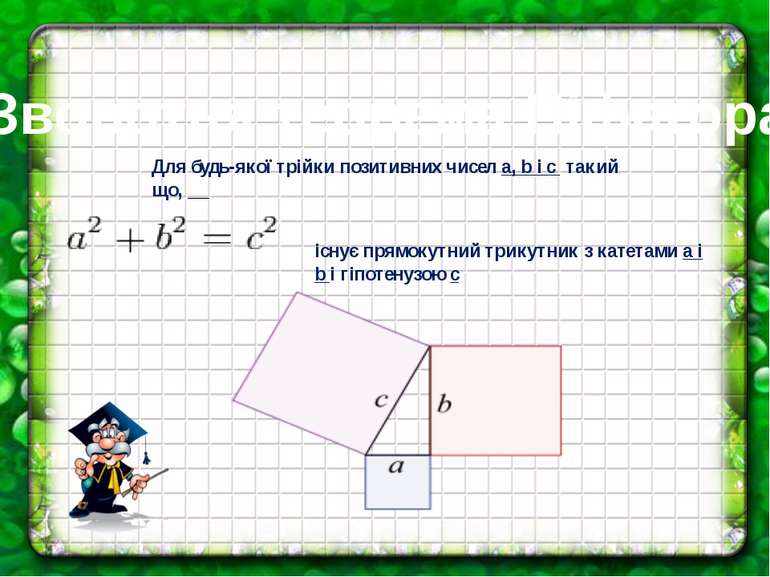
Зворотня теорема Піфагора Для будь-якої трійки позитивних чисел а, b i c такий що, iснує прямокутний трикутник з катетами а i b і гіпотенузою c

Доведення На даний момент у науковій літературі зафіксовано 367 доказів даної теореми . Ймовірно, теорема Піфагора є єдиною теоремою з настільки значним числом доказів. Таке різноманіття можна пояснити лише фундаментальним значенням  теореми для  геометрії. Зрозуміло , концептуально всі їх можна розбити на мале число класів . Найвідоміші з них: докази методом площ , аксіоматичні і екзотичні докази ( наприклад , за допомогою диференціальних рівнянь ).

Через подібні трикутники Наступне доказ алгебричного  формулюваня - найбільш просте із доказів, що будуються безпосередньо з аксіом. Зокрема, воно не використовує поняття площі фігури. Нехай ABC- є прямокутний трикутник з прямим кутом C.  Проведемо висоту з C позначимо її підстава через H.  Трикутник ACH подібний трикутнику ABC  з двох кутах.  Аналогічно, трикутник CBH подібний ABC.  ввівши позначення

отримуємо що еквівалентно Склавши, отримуємо або що потрібно було довести

Доказ через рiвнодоповнянiсть 1) Розташуємо чотири рівних прямокутних трикутника так як показано намалюнку

2) Чотирикутник зі сторонами з є квадратом, оскільки сума двох гострих кутів 90°, а розгорнутий кут - 180 градусів. 3)Площа всієї фігури рівна, з одного боку, площі квадрата зі стороною (а + б), аз іншого боку, сумі площ чотирьох трикутників і площі внутрішнього квадрата. Що й було потрібно довести.

Доказ Евкліда Розглянемо креслення зліва. На ньому ми побудували квадрати на сторонах прямокутного трикутника і провели з вершини прямого кута З променi перпендикулярно гіпотенузі AB, він розтинає квадрат ABIK, побудований на гіпотенузі, на два прямокутника - BHJI і HAKJ відповідно. Виявляється, що площі даних прямокутників в точності дорівнюють площам квадратів,побудованих на відповідних катетах.

. Доведемо тепер, що площа трикутника ACK також дорівнює половині площі квадрата DECA. Єдине, що необхідно для цього зробити, - це довести рівність трикутників ACK і BDA (так як площа трикутника BDA дорівнює половині площі квадрата за вказаною вище властивості). Рівність  очевидно: трикутники рівні за двома сторонами і куту між ними. Саме - AB =AK, AD = AC - рівність кутів CAK і BAD легко довести методом руху:повернемо трикутник CAK на 90 ° проти годинникової стрілки, тоді очевидно, що відповідні сторони двох розглянутих трикутників співпадуть (з огляду на те, що кут при вершині квадрата - 90 °). Дане доказ також отримало назву «Піфагорові штани».

Дякую за увагу!