Презентація на тему:
Союз гіпотенузи та катетів. Теорема Піфагора

Проект Союз гіпотенузи та катетів. Теорема Піфагора

Не тільки сама істина дає впевненість, але й пошук її. Б. Паскаль

Тип проекту Пізнавальний, дослідницький, творчий

Мета проекту: - поглибити та систематизувати знання учнів про погоду та її елементи; - формувати обчислювальні навички учнів, розвивати самостійність мислення, вчити об’єктивно оцінювати себе і коригувати свою діяльність та інших учнів в ході виконання проректу; - формувати в учнів вміння здійснювати вибір навчально – пізнавального завдання; вміння осмислювати й використовувати інформацію з різних джерел; вміння співпрацювати в групах, проявляти ініціативу; робити висновки; - виробити у школярів практичні навички під час використання теореми Піфагора; - виховувати спостережливість, науковий підхід , та любов до математики.

«Нероби ніколи того, що не знаєш, але вчись усьому, що потрібно знати, і тоді будеш вести спокійне життя.» Піфагор. Епіграф

Ключове питання: Чому потрібно вчити теорему Піфагора?  

Задачі проекту

Мета проекту: поглибити та систематизувати знання учнів про прямокутний трикутник та його елементи; формувати обчислювальні навички учнів, розвивати самостійність мислення, вчити об’єктивно оцінювати себе і коригувати свою діяльність та інших учнів в ході виконання проректу; формувати в учнів вміння здійснювати вибір навчально – пізнавального завдання; вміння осмислювати й використовувати інформацію з різних джерел; вміння співпрацювати в групах, проявляти ініціативу; робити висновки; виробити у школярів практичні навички під час використання теореми Піфагора; виховувати спостережливість, науковий підхід , та любов до математики.

Опис проекту Проект пропонується для реалізації з учнями 8 класу під час вивчення теми «Теорема Піфагора». Даний проект об’єднує історію, математику, географію та інформатику. У ході практичної діяльності учні повинні дослідити біографію відомого вченого, розглянути його знаменну теорему, способи її доведення і застосування для розв’язання задач. Також під час роботи над проектом учні повинні дослідити теорему Піфагора, використовуючи деякі способи її доведення. Працюючи над проектом, учні розширюють і поглиблюють свої знання з геометрії . Клас поділено на чотири групи «біоргафи», «теоретики», «практики», «лірики»

Етапи роботи над проектом 1. об’єднання учнів у групи за інтересами; 2. розподіл обов’язків; 3. пошук інформації; оформлення матеріалів; 4. пошук відповідей на тематичні питання, узагальнення результатів, досліджень і створення звіту у вигляді презентації; відгуків, фото;

Разом навчатися не тільки легше Й цікавіше, але й значно ефективніше. Є. С. Полат. «Біографи». Піфагор був філософом і математиком. Працював над властивостями цілих чисел. Інформатор цілого покоління, Філосовії навчав своїх учнів, Арифметику вивчав, Геометрія без нього, як без рук, Організував «піфагорійський союз» та школу для дітей, Релігії у ній навчав.

Вислови Піфагора 1) Роби лише те, що в результаті не засмутить тебе і не примусить каятися. 2) Не роби ніколи того, чого ти не знаєш. Але навчися усього, що варто знати, і тоді будеш вести спокійне життя. 3) Не зневажай здоров’ям свого тіла. Доставляй йому вчасно їжу і питво, і вправи, без яких воно бідує. 4) Привчайся жити просто, без розкоші. 5) Не закривай очей, коли хочеться спати, не проаналізувавши успіх своїх вчинків за минулий день. 6) Не порушуй справедливість. 7) Не сідай на подушку (тобто не зупиняйся на досягнутому). 8) Не гризи свого серця (тобто не піддавайся меланхолії). 9) Не поправляй вогню мечем (тобто не дратуй тих, хто і без того в гніві). 10) Не приймай під свій дах балакунів і легковажних людей. 11) Усе впорядковується відповідно до чисел. 12) Лише не благородна людина здатна в очі хвалити, а поза очі злословити. 13) Тимчасова невдача краще тимчасової удачі. 14) Твори велике, не обіцяючи великого. 15) Живи з людьми так, щоб твої друзі не стали недругами, а недруги стали д рузями.

«Теоретики» «Немає більш надійного способу доказу, ніж спосіб математиків, які підтверджують виведені формули прикладами й перевіркою на практиці» М.В. Ломоносов.  

Теорема Піфагора: «Сума площ квадратів, побудованих на катетах прямокутного трикутника, дорівнює площі квадрата, побудованого на гіпотенузі».

Різні способи доведення теореми Піфагора 1.спосіб доведення теореми Піфагора. Індійський математик Бхаскара ІІ подав його у формі креслення, під яким було написано лише одне слово „Дивись!”. a b a a a b b b b b b a b a a c a c c c

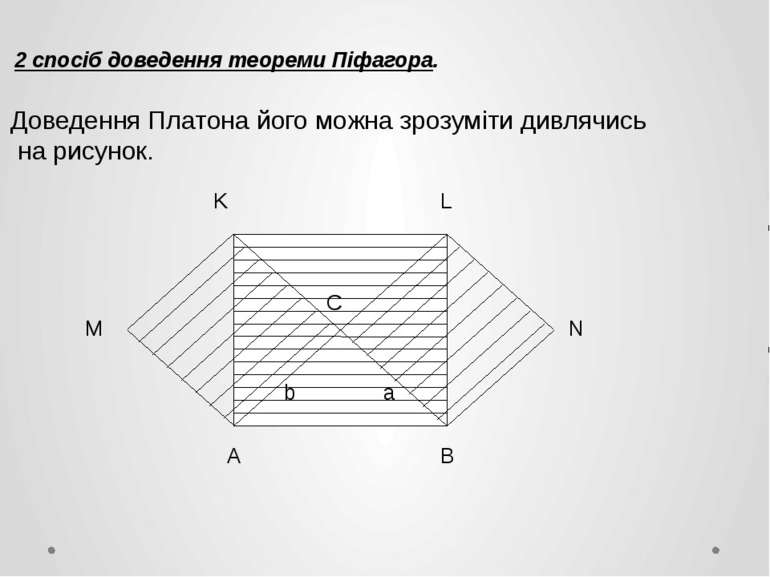
2 спосіб доведення теореми Піфагора. Доведення Платона його можна зрозуміти дивлячись на рисунок. K L M N A B C a b

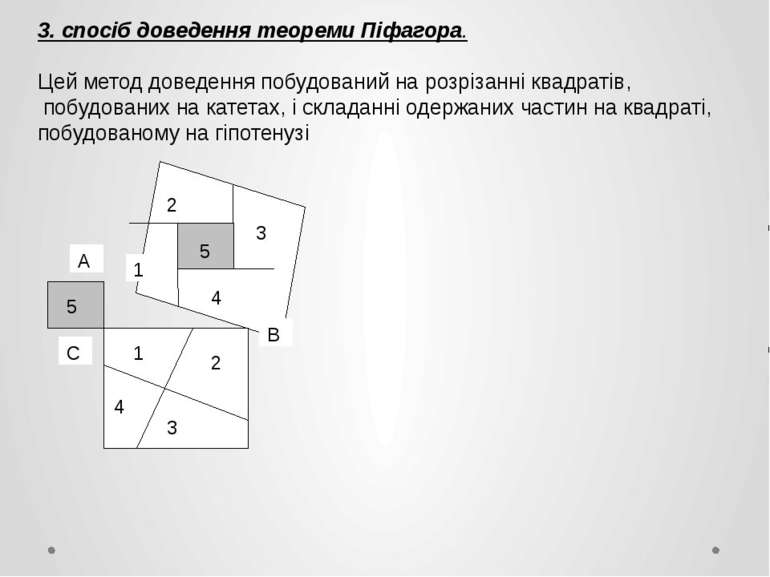
3. спосіб доведення теореми Піфагора. Цей метод доведення побудований на розрізанні квадратів, побудованих на катетах, і складанні одержаних частин на квадраті, побудованому на гіпотенузі A C B 5 5 1 2 4 3 1 4 2 3

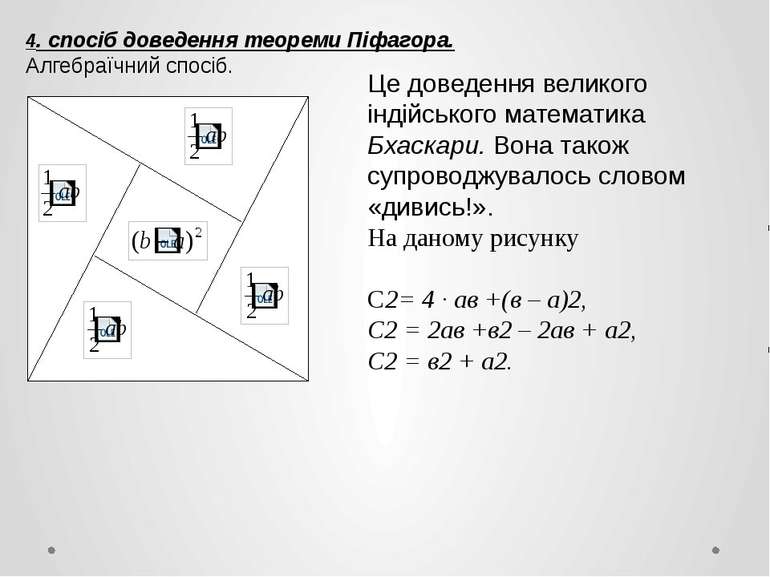
4. спосіб доведення теореми Піфагора. Алгебраїчний спосіб. Це доведення великого індійського математика Бхаскари. Вона також супроводжувалось словом «дивись!». На даному рисунку С2= 4 ∙ ав +(в – а)2, С2 = 2ав +в2 – 2ав + а2, С2 = в2 + а2.  

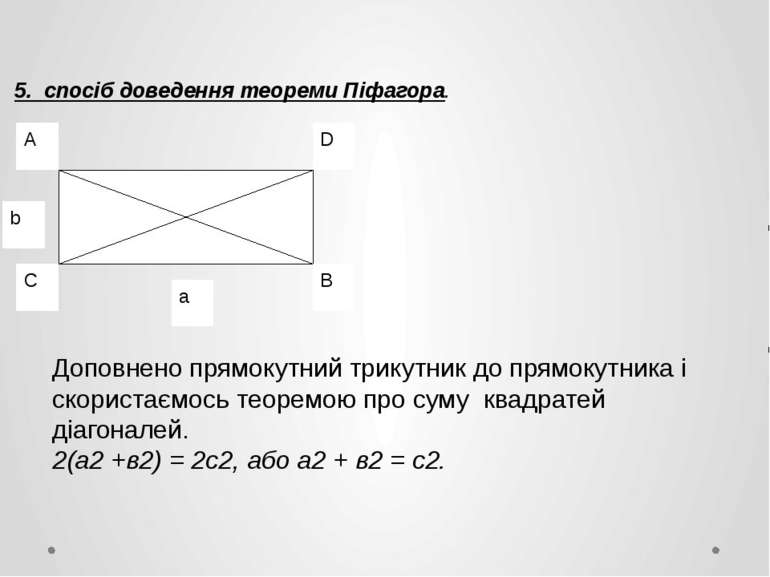
5. спосіб доведення теореми Піфагора. Доповнено прямокутний трикутник до прямокутника і скористаємось теоремою про суму квадратей діагоналей. 2(а2 +в2) = 2с2, або а2 + в2 = с2. b a A C D B

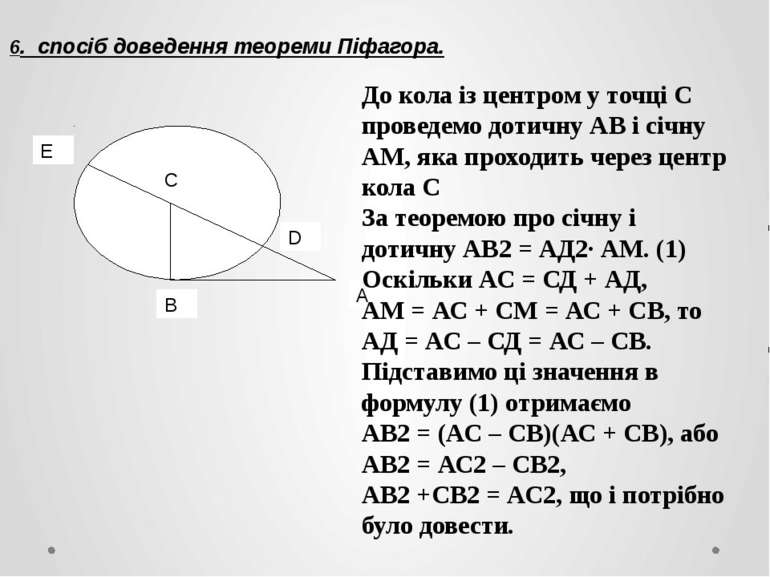
6. спосіб доведення теореми Піфагора. До кола із центром у точці С проведемо дотичну АВ і січну АМ, яка проходить через центр кола С За теоремою про січну і дотичну АВ2 = АД2∙ АМ. (1) Оскільки АС = СД + АД, АМ = АС + СМ = АС + СВ, то АД = АС – СД = АС – СВ. Підставимо ці значення в формулу (1) отримаємо АВ2 = (АС – СВ)(АС + СВ), або АВ2 = АС2 – СВ2, АВ2 +СВ2 = АС2, що і потрібно було довести.     B A E C D

«Практики».   Усе, що я пізнаю, я знаю, для чого Це мені потрібно, де і як я можу ці Знання застосовувати. В. Кильпатрик Ці задачі не прості, Застосуєш їх в житті. Щоб їх добре розв’язати, Геометрію треба знати.  

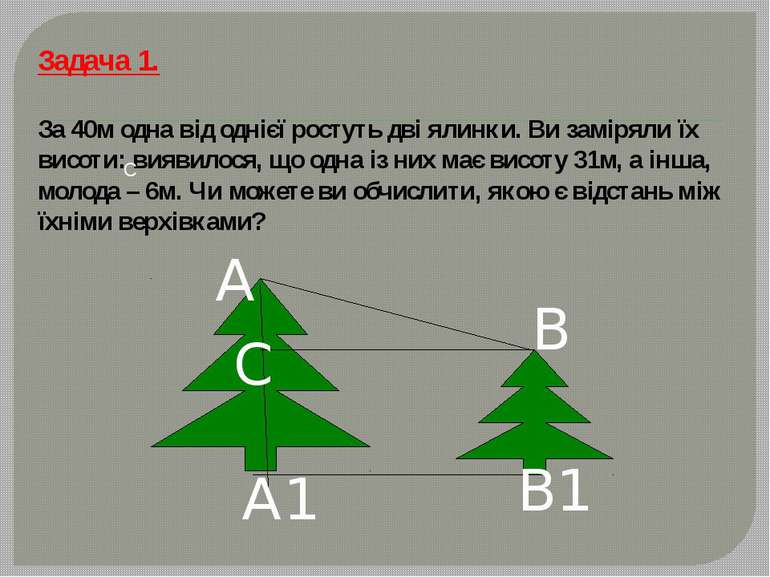
Задача 1. За 40м одна від однієї ростуть дві ялинки. Ви заміряли їх висоти: виявилося, що одна із них має висоту 31м, а інша, молода – 6м. Чи можете ви обчислити, якою є відстань між їхніми верхівками? C А В С А1 В1

Задача2. Над озером тихим Висотою із пів фута підіймалася лотоса квітка, яка росла одинокою. Та вітер скаженим поривом Відніс її в бік. І не стало видно квітки над водою. Знайшов її рибалка ранньою весною В двох футах від місця її росту. І так, пропоную я вам запитання: Яка в цьому місці глибина озера?

Задача 3. Знайти довжину драбини, прикладеної до будинку, якщо один її кінець находиться на відстані 4м від будинку, а другий на зіткненні стіни і даху. Висота будинку дорівнює 8м. M P K

Задача про тополю. На березі річки тополя росла І вітру порив її стовбур зламав. Тополя упала і стовбур її Кут прямий з течією ріки утворив. Пам’ятай, в тому місці ріка Чотири фути була шириною. Верхівка схилилась до краю, Залишивши три фути всього над водою. Прошу, тепер швидше скажи мені ти: Тополя якої була висоти?

Задача. «Стрибок мавпи» На дереві сиділи дві мавпочки: одна на самій верхівці дерева, інша на висоті 10 ліктів від землі. Другій мавпочці захотілося напитися води з джерела, що знаходиться на відстані 40 ліктів від дерева. Вона злізла із дерева і пострибала до води. У той самий час перша зістрибнула з дерева і потрапила до цього ж джерела. Обидві мавпочки подолали одинакову відстань. Визначіть з якої висоти зістрибнула мавпочка

Задача «Зламана пальма» Пальма, що ма 40 ліктів висоту було зламано вітром. Її верхівка торкнулася землі за 20 ліктів від основи стовбура. Скажіть, на якій відстані було зламано пальму.

Задача «Дві вежі» Дві вежі висотою 30 і 40 футів розміщені на відстані 50 футів одна від одної. Між ними знаходиться фонтан, до якого одночасно з верхівок веж з одинаковою швидкістю вилетіли два голуби. Визначте яка відстань від фонтана до кожної з двох веж, якщо голуби долетіли одночасно.

«Лірики». «Не в кількості знань полягає наука, а в повному розумінні й майстерному застосуванні всього того, що знаєш» Дістервег.  

Підбиття підсумків проекту Хоча чужі знання можуть нас чогось навчити Мудрим стаєш лише власною мудрістю. М. Монтен

Життя – театр, а всі ми в нім актори, Ми знаємо багато різних див, Та пам’ятати будем Піфагора, Що теорему «золоту» створив. Вивчай в житті ще й інші теореми, Щоб звався ти ученим джентльменом, То й з розумом не матимеш проблеми І виростеш культурним бізнесменом. Сьогодні все. Вам, друзі , на прощання Рекомендовано домашнєє завдання, Над геометрією хай ніхто не плаче, А краще хай розв’язує задачі.

Ось і закінчився наш проект. Час невпинно й швидко так летить. Ви до знань зробили новий крок. Хай у всьому завжди вам щастить! Дякую, що працювали гарно, Часу ви не витрачали марно, Свої сили і знання доклали. І проект свій збодували.