Презентація на тему:
Трапеція. Теорема Фалеса

Навчальна презентація до уроку 17 “Трапеція” Тема1.2. Трапеція. Теорема Фалеса

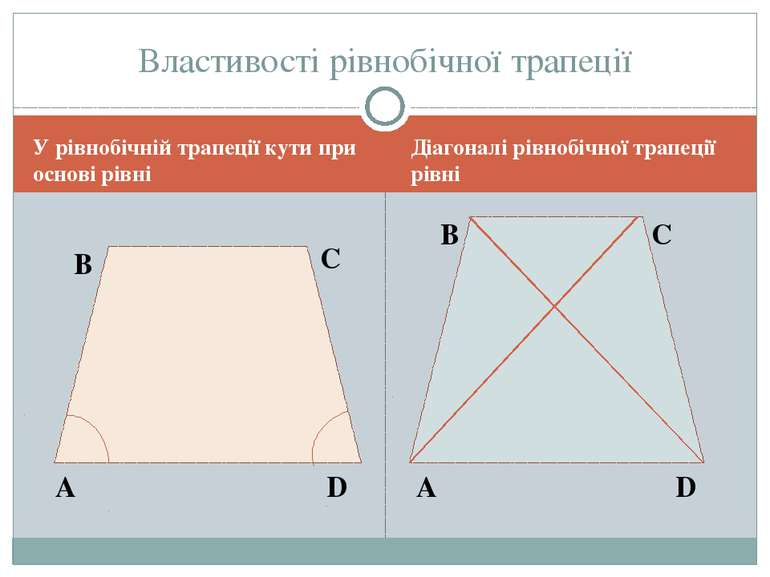
У рівнобічній трапеції кути при основі рівні Діагоналі рівнобічної трапеції рівні Властивості рівнобічної трапеції А B C D А D B C

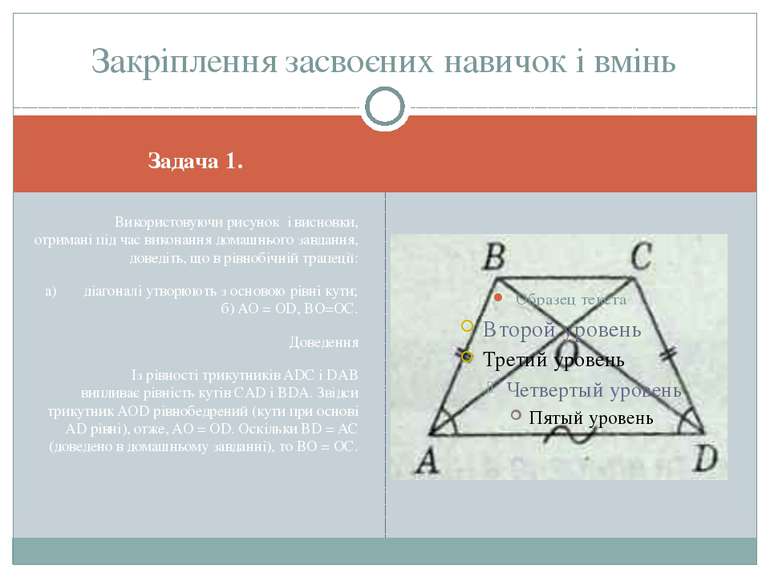
Задача 1. Використовуючи рисунок і висновки, отримані під час виконання домашнього завдання, доведіть, що в рівнобічній трапеції: а) діагоналі утворюють з основою рівні кути; б) AO = OD, BO=ОС. Доведення Із рівності трикутників ADC і DAB випливає рівність кутів CAD і BDA. Звідси трикутник AOD рівнобедрений (кути при основі AD рівні), отже, AO = OD. Оскільки BD = АС (доведено в домашньому завданні), то ВО = ОС. Закріплення засвоєних навичок і вмінь

Задача 2. У рівнобічній трапеції ABCD AD ∥ ВС, AD = а, ВС = b (а > b), ВК ⊥ AD, CN ⊥AD. Доведіть, що: a) АК = DN =(a-b):2 ; б) AN = DK = (a+b):2. Доведення а) ∆ABK=∆DCN за гіпотенузою та катетом, отже, AK = ND. Чотирикутник KBCN — прямокутник (ВС∥KN , BK∥CN, ∠BKN = ∠CNK = 90°). Звідси KN = ВС = b. Таким чином, АК + ND =а—Ь. З рівності відрізків АК і ND випливає, що АК = ND = =(a-b):2. б) KD = KN + ND = b + =(a-b):2 =(a+b):2 . Аналогічно AN = (a+b):2 Закріплення засвоєних навичок і вмінь

Задача 3. Доведіть, що в рівнобічній трапеції, діагоналі якої є взаємно перпендикулярними, висота дорівнює півсумі основ. Доведення Нехай ABCD — рівнобічна трапеція, AD ∥ BC, AB = CD. Проведемо висоту ВК (ВК ⊥AD). Оскільки ∠AOD = 90° за умовою і ∠ OAD = ∠ ODA = 45° за властивістю рівнобічної трапеції, то й у трикутнику BKD (∠ BKD = 90°) ∠ KBD = 45° . Тому трикутник ВKD — рівнобедрений, отже, ВК = KD). Але, як було доведено, KD =(AD+DC):2 тоді й ВК = (AD+DC):2 . Закріплення засвоєних навичок і вмінь

Варіант І 1). Діагональ рівнобедреної трапеції утворює з основою кут 32°, а її бічна сторона дорівнює меншій основі. Знайдіть кути трапеції. 2). Більша основа рівнобедреної трапеції дорівнює 18 см, а її діа гональ є бісектрисою гострого кута трапеції. Знайдіть меншу основу трапеції, якщо її периметр дорівнює 54 см. Відповіді до самостійної роботи Варіант І. 64°, 116°, 116°, 64°; 2. 12 см.   Варіант II 1). У рівнобедреній трапеції діагональ дорівнює більшій основі та утворює з нею кут 38°. Знайдіть кути трапеції. 2). У рівнобедреній трапеції діагональ є бісектрисою кута при осно ві. Більша основа трапеції дорівнює 26 см, а периметр — 50 см. Знайдіть меншу основу трапеції. Відповіді до самостійної роботи Варіант II. 71°, 109°, 109°, 71°; 2. 8 см. Самостійна робота Кожне завдання оцінюється в 6 балів.

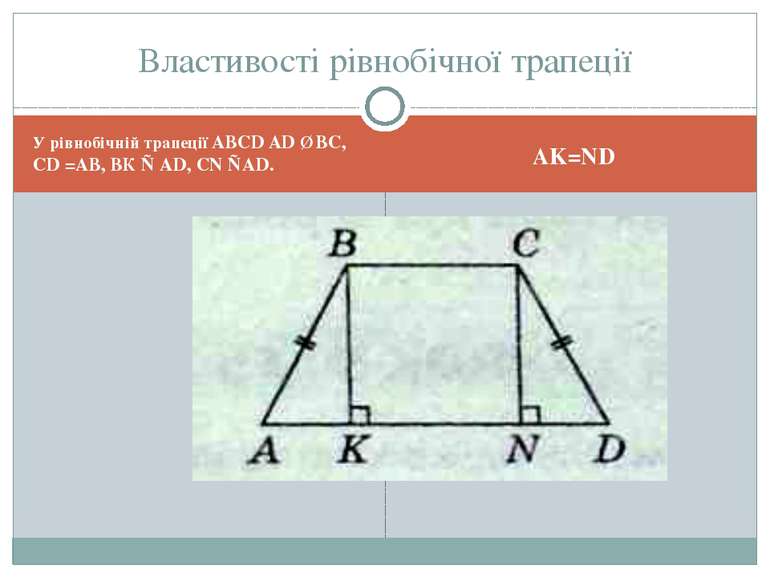
У рівнобічній трапеції ABCD AD ∥ ВС, CD =AВ, ВК ⊥ AD, CN ⊥AD. AK=ND Властивості рівнобічної трапеції