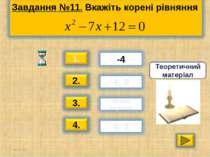
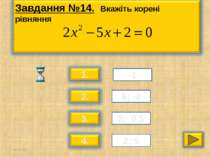
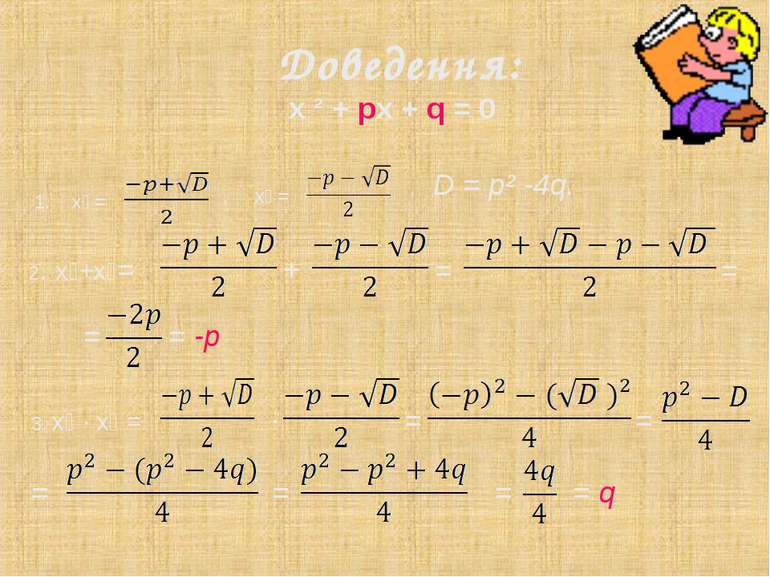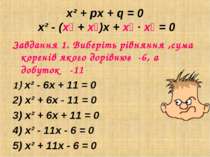Презентація на тему:
"Теорема Вієта"

Теорема Вієта

Дано: х₁ и х₂ - корені рівняння Сума коренів зведеного квадратного рівняння дорівнює другому коефіцієнту, взятому з протилежним знаком, а добуток коренів дорівнює вільному члену. Довести:

План доведення: Записати формули для знаходження x₁и x₂; Знайти суму коренів: x₁+ x₂; Знайти добуток коренів: x₁· x₂.

Доведення: х ² + pх + q = 0 1. х₁ = , х₂ = = = = -p 3. x₁ ∙ x₂ = ∙ = = = , D = p² -4q. = = = q 2. x₁+x₂= + =

Що дозволяє знаходити доведена теорема? Що повинно бути відомо до застосування теореми?

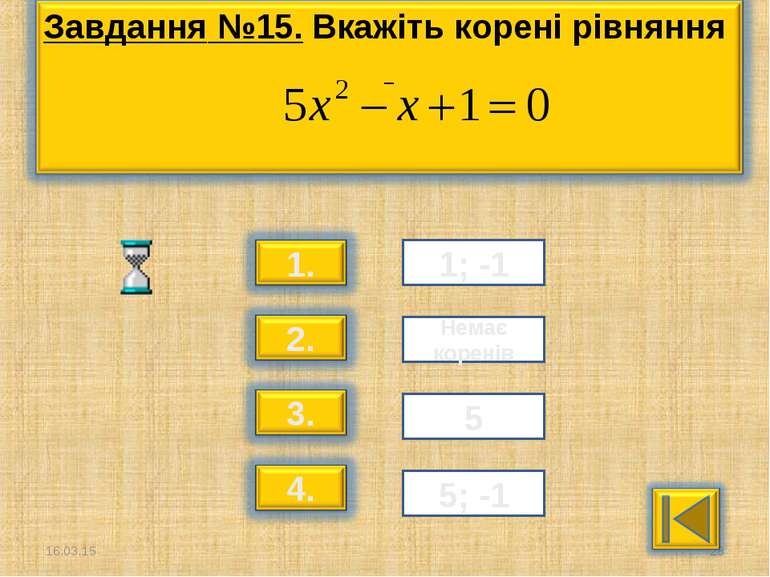
x² + px + q = 0 x² - (х₁ + х₂)х + х₁ ∙ х₂ = 0 Завдання 1. Виберіть рівняння ,сума коренів якого дорівнює -6, а добуток -11 х² - 6х + 11 = 0 х² + 6х - 11 = 0 х² + 6х + 11 = 0 х² - 11х - 6 = 0 х² + 11х - 6 = 0

Завдання 2. Якщо х₁ = -5 и х₂ = -1 - корені рівняння х² + px +q = 0, то 1) p = -6, q = 5 2) p = 5, q = 6 3) p = 6, q = 5 4) p = -5, q = -6 5) p = 5, q = -6 6) p = -6, q = -5

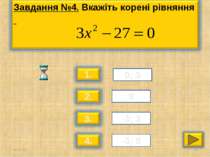
Для кожного рівняння вкажіть, якщо це можливо суму і добуток коренів х² – 2х – 8 = 0 Для кожного рівняння спробуйте підібрати два числа х₁ і х₂ так, щоб виконувались отримані рівності. 2. х² + 7х + 12 = 0 3. y² – 8y – 9 = 0 D > 0, p = -2, q = -8 x₁ + x₂ = 2 x₁ ∙ x₂ = -8 D > 0, p = 7, q = 12 x₁ + x₂ = -7 x₁ ∙ x₂ = 12 D > 0, p = -8, q = -9 y₁ + y₂ = 8 y₁ ∙ y₂ = -9 x₁ = -2 x₂ = 4 2 ∙ (-4) -2 ∙ 4 1 ∙ (-8) -1 ∙ 8 x₁ = -3 x₂ = -4 y₁ = -1 y₂ = 9

Розв’яжіть рівняння за допомогою теореми Віета x2-5x+6=0 x2+7x+12=0 x2+2008x-2009=0

x2 - 5x+6=0; x1+x2=5; x1=2 x1x2=6; x2=3 x2+7x+12=0; x1+x2=-7; x1=-3 x1x2=12; x2=-4 x2+2008x-2009=0; x1+x2=-2008; x1x2=-2009 x1=-2009; x2=1

Теорема Вієта Числа х₁ и х₂ є коренями квадратного рівняння aх² + bх + с =0 тоді і тільки тоді, коли х₁ + х₂ = х₁ ∙ х₂ = По праву достойна в стихах быть воспета О свойствах корней теорема Виета. Что лучше, скажи, постоянства такого: Умножишь ты корни — и дробь уж готова? В числителе с, в знаменателе а А сумма корней тоже дроби равна. Хоть с минусом дробь, что за беда! В числителе в, в знаменателе а.

«Квадратні рівняння»».

* * Теоретичний матеріал

* * -5; 5 -5; 0 25 0; 5

* *

* * 0; 3 9 -3; 3 -3; 0

* * -2; 2 4 2 2; 0

* * -2; 2 4 2 2; 0

* * Теоретичний матеріал

* * 0 1 2 Безліч

* * Безліч 2 0 1

* * 2 0 1 Безліч

* * 2 Безліч 1 0

* * Теоретичний матеріал

* * -2; 3 Немає коренів -4 0; 5

* * 3 -3; 3 0; 3 Немає коренів

* * 2; 5 2; 0.5 5; -2 -1

* * 1; -1 Немає коренів 5 5; -1

* * Квадратним називається рівняння виду ax² + bx + c = 0, де х - змінна; a,b,c – дані числа, причому а≠0. Якщо а, або b дорівнює нулю, то рівняння називають неповним. Розв’язування: 1. Рівняння виду ax²=0; x²=0; х=0. 2. Рівняння виду ax² + bx =0; х(ах+b)=0; х=0, або х= -b/а. 3. Рівняння виду ax²+с =0; x²= -с/а; х= .

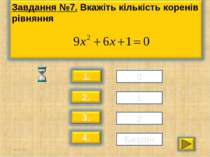
* * Квадратним називається рівняння виду ax² + bx + c = 0, де х - змінна; a,b,c – дані числа, причому а≠0. Вираз b²- 4ас називають дискримінантом даного квадратного рівняння і позначають D. Якщо D < 0, то дане рівняння не має коренів. Якщо D > 0, то дане рівняння має 2 різні корені. Якщо D = 0, то дане рівняння має 1 корінь.

* * Квадратним називається рівняння виду ax² + bx + c = 0, де х - змінна; a,b,c – дані числа, причому а≠0. Розв’язування повного квадратного рівняння Шукаємо дискримінант D =b²- 4ас. Якщо D = 0, то дане рівняння має корінь Якщо D < 0, то дане рівняння не має коренів. Якщо D > 0, то корені шукаємо за формулою: