Презентація на тему:
Степенева функція з натуральним показником

Алгебра і початки аналізу. 10 клас (за підручником Мерзляк А. Г.)

Тема уроку: Степенева функція з натуральним показником

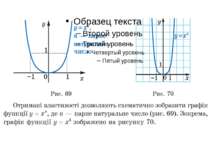
Степенева функція Властивості і графіки функцій y = x і y = x2 знайомі вам з попередніх класів. Ці функції є окремими випадками функції y = x n, n ∈ N, яку називають степеневою функцією з натуральним показником. Оскільки вираз x n, n ∈ N, має зміст при будь-якому x, то областю визначення степеневої функції з натуральним показником є множина R. Очевидно, що розглядувана функція має єдиний нуль x = 0. Подальше дослідження властивостей функції y = x n, n ∈ n, проведемо для двох випадків: n — парне натуральне число і n — непарне натуральне число.

n = 2k, k ∈ N. При k = 1 отримуємо функцію y = x2. Оскільки при будь-якому x вираз x2k набуває тільки невід’ємних значень, то область значень розглядуваної функції не містить жодного від’ємного числа. Можна показати, що для будь-якого a ≥ 0 існує таке значення аргументу x, що x2k = a.

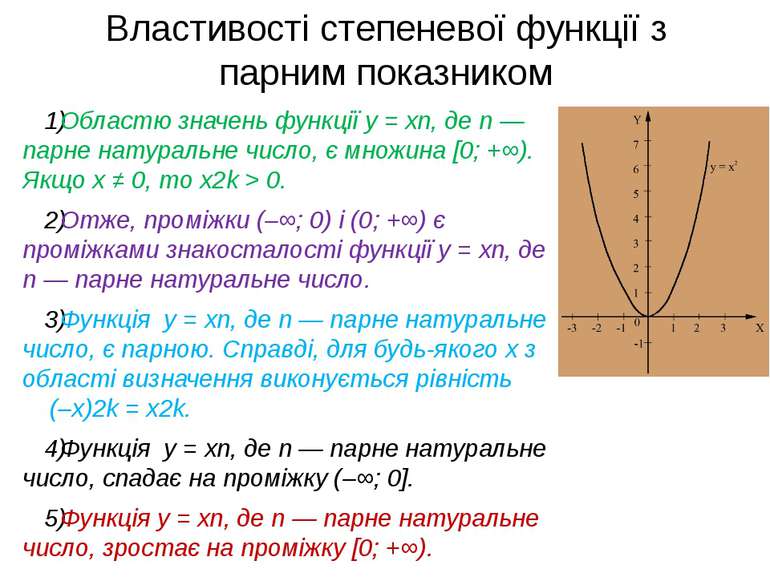
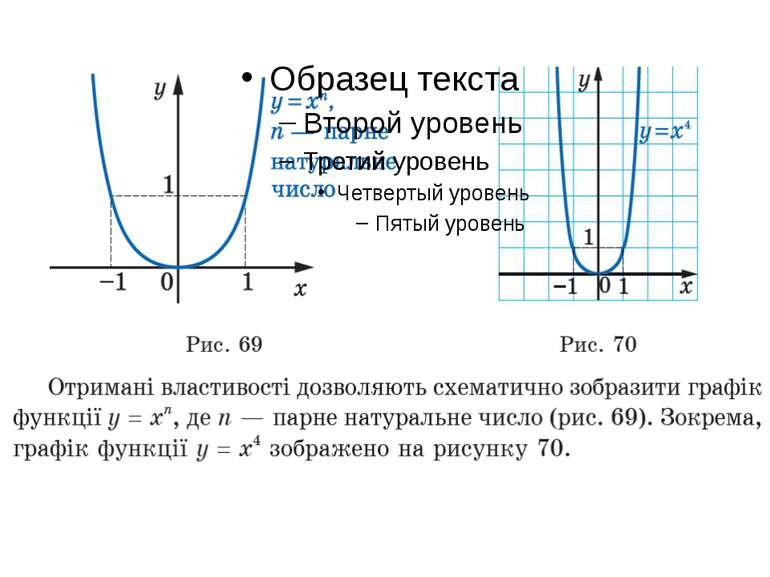
Властивості степеневої функції з парним показником Областю значень функції y = xn, де n — парне натуральне число, є множина [0; +∞). Якщо x ≠ 0, то x2k > 0. Отже, проміжки (–∞; 0) і (0; +∞) є проміжками знакосталості функції y = xn, де n — парне натуральне число. Функція y = xn, де n — парне натуральне число, є парною. Справді, для будь-якого x з області визначення виконується рівність (–x)2k = x2k. Функція y = xn, де n — парне натуральне число, спадає на проміжку (–∞; 0]. Функція y = xn, де n — парне натуральне число, зростає на проміжку [0; +∞).

n — непарне натуральне число При n = 1 отримуємо функцію y = x, властивості і графік якої були розглянуті в 7 класі. 1). D(y)=R 2). E(y)=R 3). Функція непарна 4). Функція зростаюча 5). Графік функції – пряма, що є бісектрисою І та ІІІ чвертей 6). Графік перетинає осі координат в точці (0,0) 7). Найбільшого чи найменшого значення функція немає

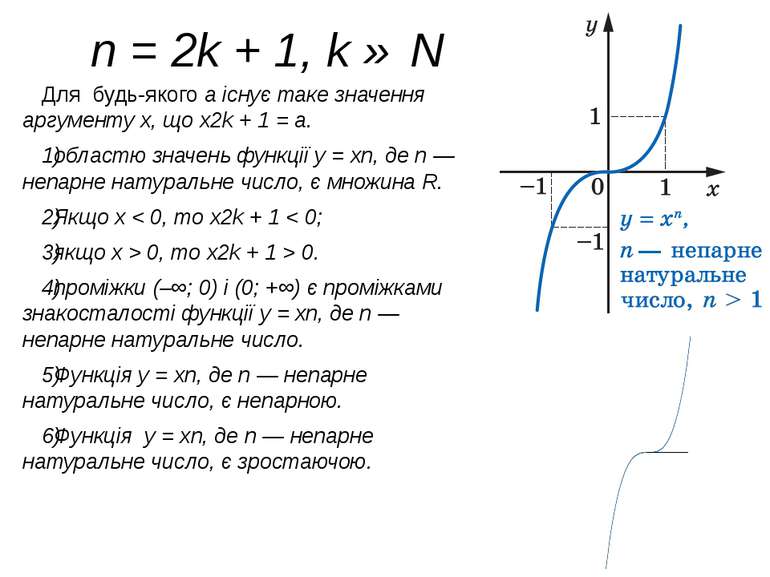
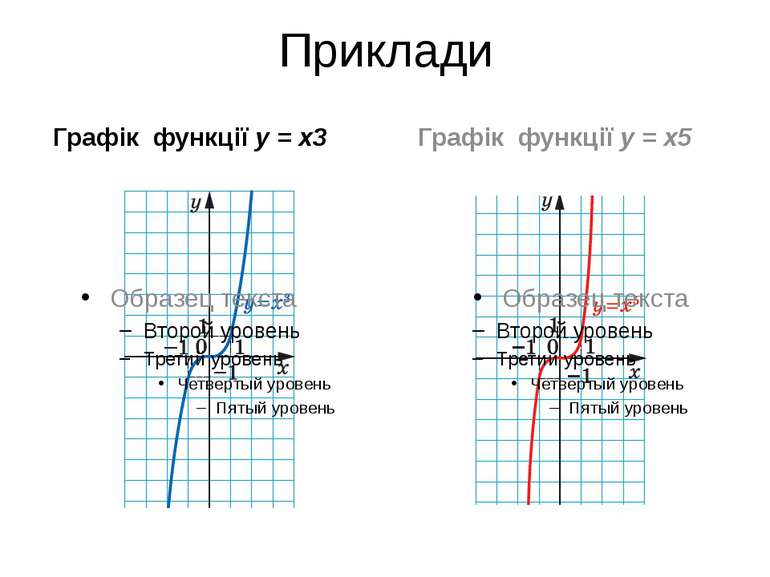
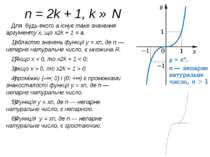
n = 2k + 1, k ∈ N Для будь-якого a існує таке значення аргументу x, що x2k + 1 = a. областю значень функції y = xn, де n — непарне натуральне число, є множина R. Якщо x < 0, то x2k + 1 < 0; якщо x > 0, то x2k + 1 > 0. проміжки (–∞; 0) і (0; +∞) є проміжками знакосталості функції y = xn, де n — непарне натуральне число. Функція y = xn, де n — непарне натуральне число, є непарною. Функція y = xn, де n — непарне натуральне число, є зростаючою.

Приклади Графік функції y = x3 Графік функції y = x5

Висновки

Первинне закріплення вивченого матеріалу Яку функцію називають степеневою функцією з натуральним показником? Яка область визначення степеневої функції з натуральним показником? Сформулюйте властивості функції y = xn, де n — парне натуральне число. Як виглядає графік функції y = xn, де n — парне натуральне число? Сформулюйте властивості функції y = xn, де n — непарне натуральне число. Як виглядає графік функції y = xn, де n — непарне натуральне число?

Тренувальні вправи

Тренувальні вправи

Тренувальні вправи

Тренувальні вправи

Домашнє завдання Читати § 9 Виконати вправи №№ 243, 245, 247, 249, 252, 255, 257, 259, 261 Повторити властивості степеневих функцій