Презентація на тему:
ПРОЕКТ «Функція»

ПРОЕКТ «Функція»

Не тільки сама істина дає впевненість, але й пошук її. Б. Паскаль  

Тип проекту Пізнавальний, дослідницький, творчий

Мета Проекту поглибити та систематизувати знання учнів функцію; формувати обчислювальні навички учнів, розвивати самостійність мислення, вчити об’єктивно оцінювати себе і коригувати свою діяльність та інших учнів в ході виконання проректу; формувати в учнів вміння здійснювати вибір навчально – пізнавального завдання; вміння осмислювати й використовувати інформацію з різних джерел; вміння співпрацювати в групах, проявляти ініціативу; робити висновки; виробити у школярів практичні навички під час побудови графіків функції; виховувати спостережливість, науковий підхід , та любов до математики.

Опис проекту Проект пропонується для реалізації з учнями 7 класу під час вивчення теми «Функція». Даний проект об’єднує математику та інші дисципліни. У сьомому класі вводиться одне з фундаментальних математичних понять – поняття функції. Тут же розглядається лінійна функція та її графік. Згодом ці відомості використовуються для графічної ілюстрації розв‘язування лінійного рівняння з однією змінною, а також системи двох лінійних рівнянь з двома змінними. Інші види функцій розглядаються у 8 – 11 класах. Клас поділено на чотири групи «історики», «теоретики», «практики», «лірики» кожна з груп протягом тижня працює над своєю частиною роботи: збирає інформацію, підбирає цікаві факти, готує коротку презентацію за змістом опрацьованого матеріалу, робить висновки.  

Задачі проекту

Етапи проведення проекту підготовчий Планування Дослідницький Презентативний

«Немає жодної галузі людського знання, куди не входили б поняття про функції та їх графічне зображення» К. Ф. Лебединцев Епіграф:

Анотація Під час роботи над проектом, учні повинні не тільки навчитися збирати первинну інформацію познайомляться поняттям «функція», навчаться знаходити область визначення та область значень функції. Удосконалять та поглиблять свої знання із теми. Виявлять зв'язок математики з іншими науками. Відкривають для себе багато нового, цікавого захоплюючого з історії математики. Навчаться захищати свій проект перед однокласниками, критично мислити , розмірковувати, робити висновки, приймати самостійні рішення.

Разом навчатися не тільки легше Й цікавіше, але й значно ефективніше. Є. С. Полат. Недостатньо лише зрозуміти задачу, треба мати бажання розв’язати її. Де є бажання, знайдеться і шлях. Д.Пойа

Функціональна лінія пронизує весь курс алгебри основної школи і розвивається у тісному зв‘язку з тотожними перетвореннями, рівняннями і нерівностями. Термін «функція» уперше зустрічається в рукописі великого німецького математика і філософа Г. Лейбніца — спочатку в рукописі (1673 р.), а потім і в друкованому вигляді (1692 р.). Латинське слово function переводиться як «здійснення», «виконання» (дієслово fungor переводиться також словом «виражати»). Лейбніц увів це поняття для назви різних параметрів, зв’язаних з положенням точки на площині. У ході переписування Лейбніц і його учень — швейцарський математик И. Бернуллі (1667—1748) «Історики» Щоб вирішити важливі справи, Не знати в житті невдач, Ми створимо проект на славу З цікавих і складних задач.

Функція – одне з найважливіших понять математики вона дає можливість досліджувати і моделювати не тільки стани, а й процеси. Дослідження процесів і явищ за допомогою функцій – один з основних методів сучасної науки. Якщо кожному значенню змінної х деякої множини D відповідає єдине значення змінної у, то змінну у називають функцією від х. Усе, що я пізнаю, я знаю, для чого Це мені потрібно, де і як я можу ці Знання застосовувати. В. Кильпатрик   «Теоретики»

Способи задання функції Табличний спосіб задання функції дуже зручний, коли область визначення функції складається зі нескінченного числа точок. Функцію задано таблично, коли в одному рядку (або стовпчику) записані всі значення аргументу, а в другому відповідні значення функції. Приклади таких таблиць: таблиця квадратів чисел, таблиця кубів чисел, таблиця основних тригонометричних функцій Наприклад, функцію у = 2х – 1 для перших пяти натуральних значень х можна задати у вигляді такої таблиці. - Область визначення даної функції: 1,2,3,4,5 - Область значень даної функції: 1,3,5,7,9 х 1 2 3 4 5 у 1 3 5 7 9

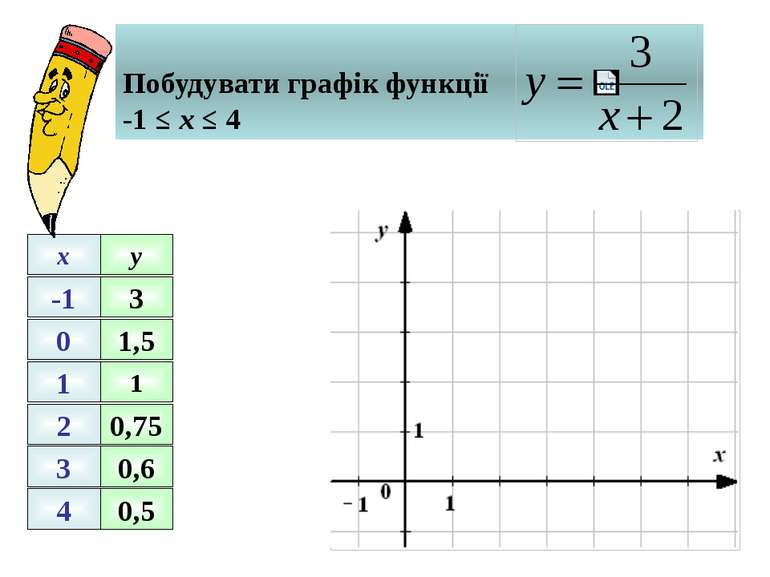
Графічний спосіб задання функції полягає в тому, що подається графік цієї функції. Для використання графіків функції використовують прямокутну систему координат хОу. Це сукупність двох взаємно перпендикулярних числових осей зі спільним початком.. Одну з осей – горизонтальну – називають віссю абсцис, або віссю іксів, або віссю Ох. Другу, вертикальну вісь, називають ординатою або віссю ігриків,. Або віссю Оу. Числа, що позначають положення точки на координатній площині хОу, називають координатами точки. Графіком функції у = f(х) називають множину точок площини хОу, абсцисами яких є значення аргументу х, а ордината – відповідні значеня у = f(х).

Словесне задання функції полягає в тому, що відповідність між х тау виражається словами. До словесного способу задання функції належить і такий, коли функція задається за допомогою кількох формул, кожна з яких діє при певних значеннях аргументу, що доводиться визначати словами.

Розглядають питання побудови графіків фукцкції та застосування їх до розв'язування вправ Графіком функції називається фігура. Яка складається з усіх точок координатної площини. Абсциси яких дорівнюють значенням аргументу, а ордината – відповідним значенням функції. Графік – це лінія, що говорить і яка може про багато що розповісти. М. Б. Балк   «Практики»

Графік функції. Графік функції - це множина всіх точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати - відповідним значенням функції. IV III II I

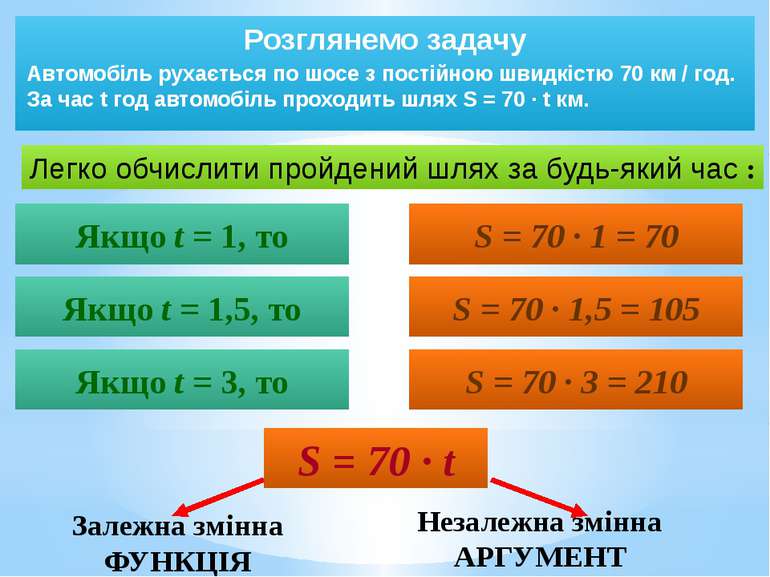
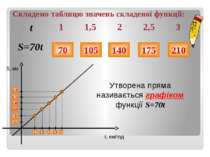
Розглянемо задачу Автомобіль рухається по шосе з постійною швидкістю 70 км / год. За час t год автомобіль проходить шлях S = 70 · t км. Легко обчислити пройдений шлях за будь-який час : Якщо t = 1, то Якщо t = 1,5, то Якщо t = 3, то S = 70 · 1 = 70 S = 70 · 1,5 = 105 S = 70 · 3 = 210 S = 70 · t Незалежна змінна АРГУМЕНТ Залежна змінна ФУНКЦІЯ

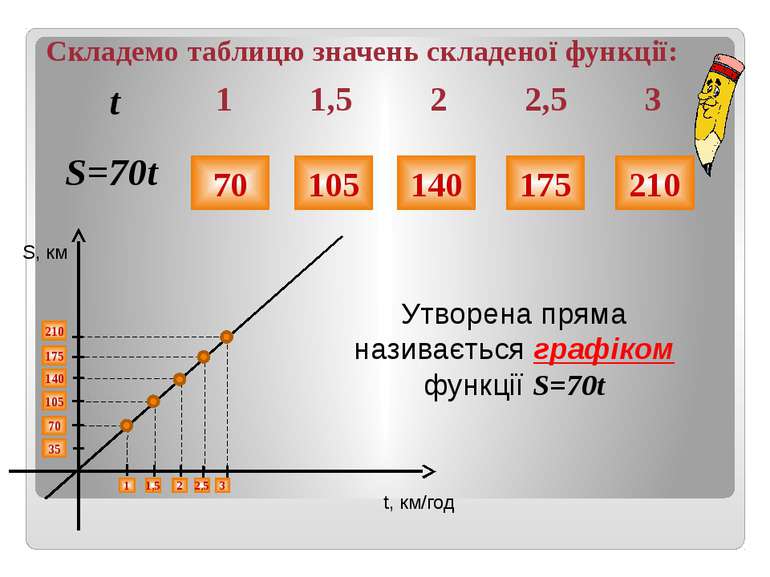
Складемо таблицю значень складеної функції: 70 105 140 175 210 70 105 140 175 210 35 1 1,5 S, км t, км/год 2 2,5 3 Утворена пряма називається графіком функції S=70t t 1 1,5 2 2,5 3 S=70t Ответы – щелчком мышки по пустому полю слайда

-1 0 1 2 3 4 x y 1 0,75 0,6 0,5 3 1,5 Побудувати графік функції -1 ≤ х ≤ 4

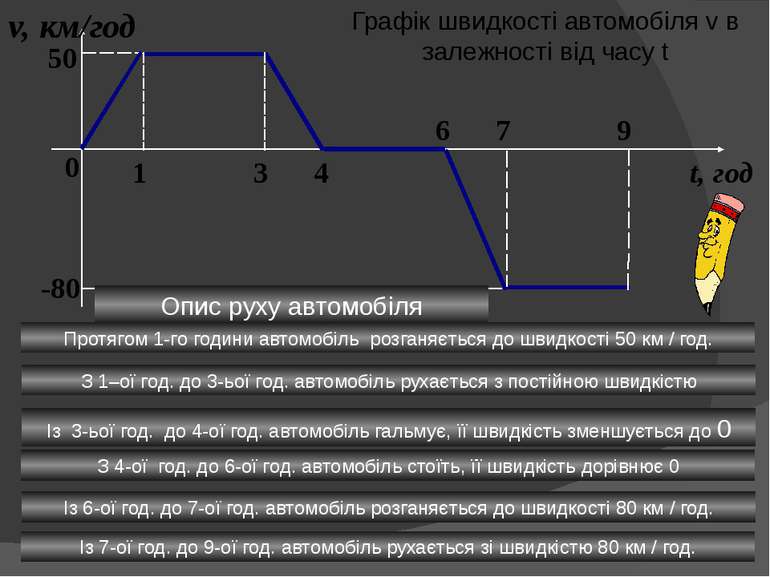
0 1 3 4 6 7 9 v, км/год t, год 50 -80 Графік швидкості автомобіля v в залежності від часу t Опис руху автомобіля Протягом 1-го години автомобіль розганяється до швидкості 50 км / год. З 1–ої год. до 3-ьої год. автомобіль рухається з постійною швидкістю Із 3-ьої год. до 4-ої год. автомобіль гальмує, її швидкість зменшується до 0 З 4-ої год. до 6-ої год. автомобіль стоїть, її швидкість дорівнює 0 Із 6-ої год. до 7-ої год. автомобіль розганяється до швидкості 80 км / год. Із 7-ої год. до 9-ої год. автомобіль рухається зі швидкістю 80 км / год.

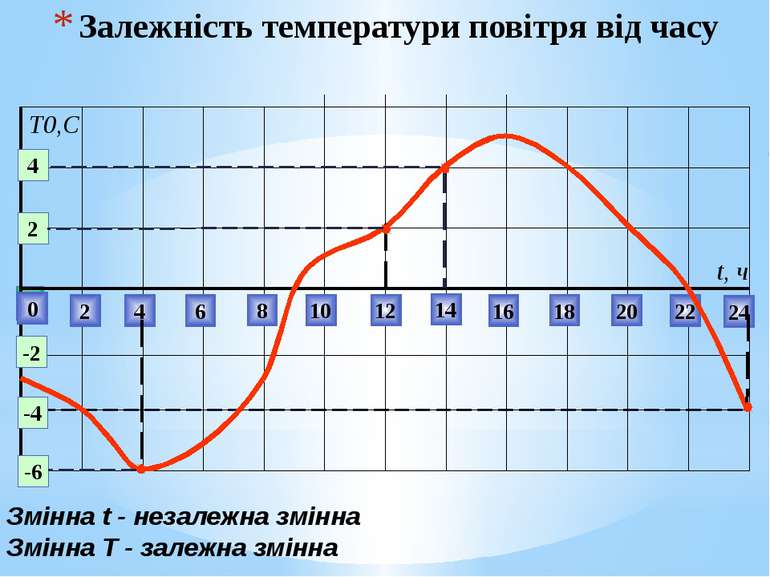
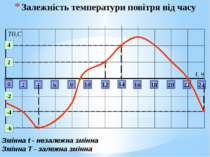
Залежність температури повітря від часу 0 2 4 6 8 10 12 14 22 24 16 18 20 t, ч 2 4 -2 -6 -4 Т0,С Змінна t - незалежна змінна Змінна T - залежна змінна

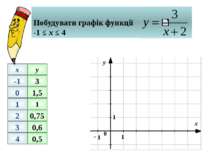
Лінійною функцією називають функцію, що задається формулою y = bx + c, де x – аргумент; с, b - константи. Її графік – пряма лінія Лінійна функція

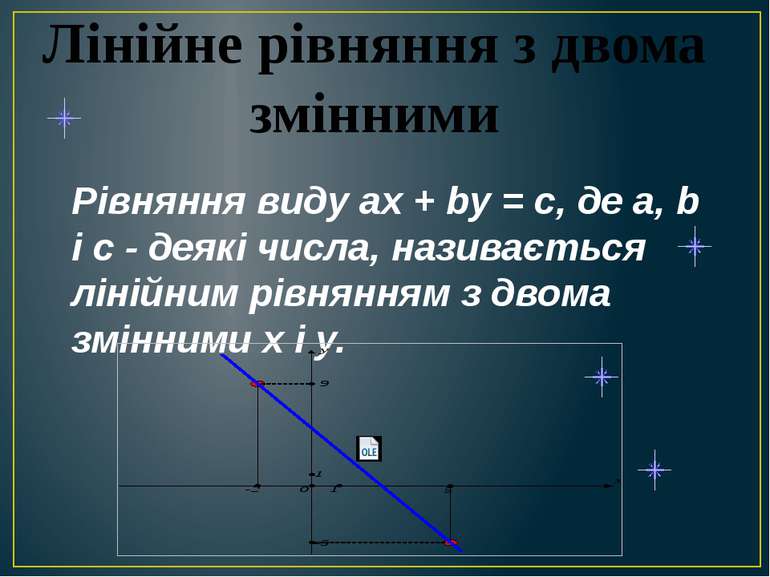
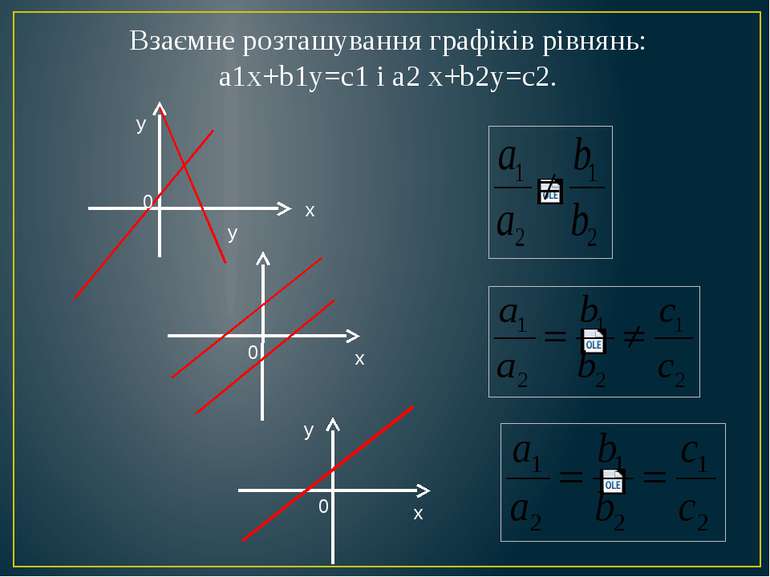
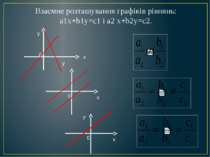
Лінійне рівняння з двома змінними Рівняння виду ах + bу = с, де а, b і с - деякі числа, називається лінійним рівнянням з двома змінними х і у.

Якщо а, b і с не дорівнюють нулю, то пряма проходить під кутом до координатних осей і перетинає їх у двох точках.  

Якщо права частина лінійного рівняння з двома змінними дорівнює нулю, то пряма проходить через початок координат під кутом до координатних осей. -2 0 х у

Якщо коефіцієнт при змінній х = 0, а інші не дорівнюють нулю, то пряма паралельна осі х.

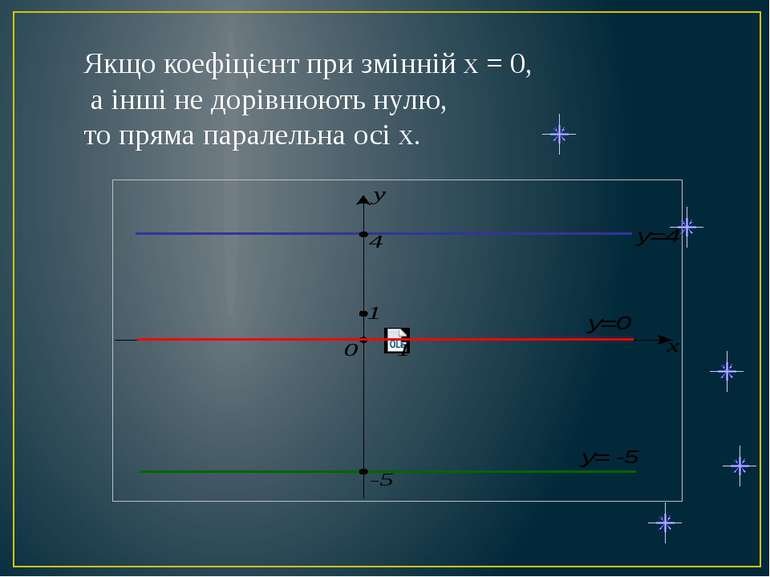
Якщо всі коефіцієнти, окрім коефіцієнта при у, не дорівнюють нулю, то пряма паралельна осі у.

Взаємне розташування графіків рівнянь: а1х+b1y=c1 і a2 x+b2y=c2. y y y x 0 x x 0 0

Як було за додекартових часів? Аргумент один тинявся по осі - Беззмістовно, нецікаво, в бідності, Бо не мав нікого в відповідності. Поруч ниділа така ж величина, Як і він; та то була вона – Та, що здатна дивні дива плодити; Лиш би з Аргументом їх узгодити. Їх Декарт уміло об’єднав, Щоб не залишалась Функція одна; Хоч вона й зробилася залежною Та наповнилася здатністю належною, І зросли можливості обох стократ, І поставили їх вчені в перший ряд, І прийшли до них повага й гідність Ось що значить – добра відповідність! «Не в кількості знань полягає наука, а в повному розумінні й майстерному застосуванні всього того, що знаєш» Дістервег «Лірики»

Підсумки проекту Хоча чужі знання можуть нас чогось навчити Мудрим стаєш лише власною мудрістю. М. Монтен «Коли ми прагнемо шукати невідоме, то стаємо кращими, мужнішими і діяльнішими за тих, хто вважає, ніби невідоме не можна знайти і немає чого шукати». Хай ця думка Платона супроводжує вас на життєвому шляху. У майбутньому ви будите будівельниками та інженерами, конструкторами та математиками, і знання, отримані на сьогоднішньому уроці, вам обов’язково знадобляться.