Презентація на тему:
Принцип парності" з курсу за вибором " Подільність цілих чисел"

Курс за вибором з математики “ Подільність цілих чисел “ 8 клас Лебединська ЗОШ I-IIIступенів №6

Який курс ми вивчаємо? Яких нових знань ви набули вивчаючи цей курс ? Матеріал з яких тем ми повторювали ? З якими методами розвязування задач на подільність ви познайомились ? Який зміст доведення методом від супротивного?

Хвилинка історії

Після закінчення олімпіади Петя і Вася порвали свої листки з завданнями олімпіади, причому Петя кожний свій шматок розриває на 3 частини, а Вася на 5 частин. Чи може в якийсь момент хоча б один з них (окремо) одержати рівно 2000 шматочків? Задача

Тема заняття: Принцип парності Мета заняття: поглибити знання про різноманітні методи розв’язування завдань на подільність цілих чисел; навчити використовувати ідею парності чисел для розв’язування завдань; повторити і узагальнити основні властивості парних і непарних чисел; повторити різні означення парних і непарних чисел, їх загальні формули запису.

Парні і непарні числа Число називається парним, якщо воно без остачі ділиться на 2. Число називається парним, якщо його можна представити у вигляді суми двох однакових доданків. Загальна формула: 2n Приклади: 2, 4, 8, 24…. Число називається непарним, якщо воно не ділиться без остачі на 2. Число називається непарним, якщо його не можна представити у вигляді суми двох однакових доданків. Загальна формула: 2n +1 Приклади: 5,9,21,43….

Властивості парних чисел Сума будь-якої кількості парних чисел завжди парна 2∙n + 2∙k + … + 2∙f + 2∙q = 2∙(n + k + … + f + q) = 2∙m  Різниця будь-якої кількості парних чисел завжди парна 2∙n – 2∙k – … – 2∙f – 2∙q = 2∙(n – k – … – f – q) = 2∙m Добуток парних чисел завжди парний 2m ∙ 2n ∙ 2k ∙ … ∙2f ∙ 2g=2∙ s∙ (m∙ n ∙ k∙ … ∙ f∙ g) Добуток кількох множників серед яких, хоча б один парний є парним

Властивості непарних чисел Сума парної кількості непарних чисел завжди парна (2∙n -1)+ (2∙k-1)+ … + (2∙f-1) + (2∙q-1) = 2∙(n + k + … + f + q)- 2s = 2∙(m-s) Сума непарної кількості непарних чисел завжди непарна 2∙n -1)+ (2∙k-1)+ … + (2∙f-1) + (2∙q-1) = 2∙(n + k + … + f + q)- 2s -1 = 2∙(m-s) – 1 Добуток парної кількості непарних множників є число парне Добуток непарної кількості непарних множників є число непарне Степінь непарного числа є непарним числом

Висновок Таким чином, парність результату не залежить від розстановки плюсів і мінусів між цілими числами, а залежить тільки від кількості непарних чисел в початковому наборі.

Задача 1 Нехай m i n - цілі числа. Доведіть, що m*n(m+n) – парне число - Нехай m і n – парні,тоді вираз mn(m+n) буде парним. - Нехай m і n – обидва непарні, тоді (m+n) – парне число, отже вираз mn(m+n) буде парним. - Нехай m і n – числа різної парності, тоді добуток mn – парний і вираз mn(m+n) буде парним

Задача 2 Петро купив загальний зошит на 96 аркушів і пронумерував всі його сторінки по порядку числами від 1 до 192. Василь вирвав з цього зошита 35 аркушів і додав всі 70 чисел, що на них були написані. Чи міг він дістати 1990? На кожному аркуші сума номерів сторінок непарна, а сума 35 непарних чисел непарна.

Задача 3 Добуток 22 цілих чисел дорівнює 1. Доведіть, що їх сума не дорівнює нулю. Серед цих чисел – парне число "мінус одиниць", а для того, щоб сума дорівнювала нулю, їх має бути рівно 11.

Ні, не можна. Серед цих чисел одне (це 2) – парне, а інші непарні. Тому в рядку, де стоїть двійка, сума чисел непарна, а в інших – парна. Чи можна скласти магічний квадрат з перших 36 простих чисел? Задача 4 2 н н н н н н н н н н н н н н н н н н н н н н н н н н н н н н н н н н н

Задача 5 В ряд записано числа від 1 до 10. Чи можна розставити між ними знаки "+" та "–" так, щоб значення отриманого виразу дорівнювало нулю? Ні, не можна. І справді, сума чисел від 1 до 10 дорівнює 55( непарне), і змінюючи в ній знаки, ми не змінюємо парність суми.

Задача 6 На площині розміщено 11 шестерень, з’єднаних одна за одною ланцюгово, чи можуть всі шестерні обертатися одночасно? Це не можливо: 1,3,5 і т.д шестерні обертаються за годинниковою стрілкою, а отже і 11. 1 і 11 обертаються в одному напрямку, що неможливо

Задача 7 Чи можна покрити шахматну дошку доміношками розміром 1x2 так, щоб вільними залишились тільки клітинки а1 і h8? Не можна. Кожна доміношка покриває одне чорне і одне біле поле, а при викиданні полів а1 і h8 чорних полів залишається на 2 менше, ніж білих.

Задача 8 На столі стоїть 7 стаканів – всі дном до верху. За один крок можна перевернути будь – які 4 стакани. Чи можна за декілька кроків досягти того, щоб усі стакани стояли правильно? Для того, щоб стакан став правильно, його треба перевернути непарну кількість раз, число стаканів теж непарне, тобто нам треба зробити непарну кількість переворотів,щоб всі стакани стали правильно, але за кожен крок ми перевертаємо парну кількість стаканів. Отже поставлене завдання виконати неможливо.

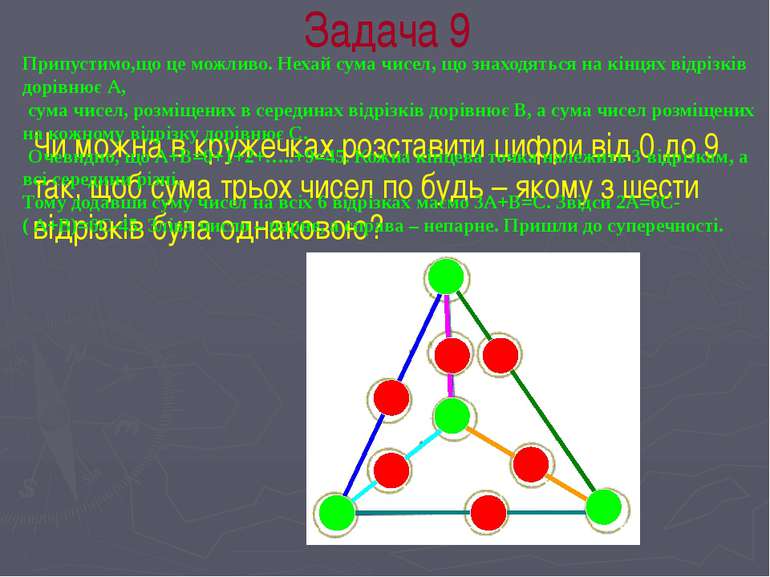
Задача 9 Чи можна в кружечках розставити цифри від 0 до 9 так, щоб сума трьох чисел по будь – якому з шести відрізків була однаковою? Припустимо,що це можливо. Нехай сума чисел, що знаходяться на кінцях відрізків дорівнює А, сума чисел, розміщених в серединах відрізків дорівнює В, а сума чисел розміщених на кожному відрізку дорівнює С. Очевидно, що А+В=0+1+2+…..+9=45. Кожна кінцева точка належить 3 відрізкам, а всі середини різні. Тому додавши суму чисел на всіх 6 відрізках маємо 3А+В=С. Звідси 2А=6С-( А+В)=6С-45. Зліва число – парне, а справа – непарне. Пришли до суперечності.

Дякую за увагу