Презентація на тему:
Поняття про площу

Площа….

Що таке площа?  Площа простої фігури – це додатна величина, числове значення яка має свої властивості.

Властивості площі: Рівні фігури мають рівні площі; Якщо фігура розбивається на частини, кожна з яких є простою фігурою, то площа всієї фігури дорівнює сумі площ її частин; Площа квадрата зі стороною, яка дорівнює одиниці вимірювання, дорівнює одиниці.

З поняттям площі діти мають справу постійно. Вже дошкільники порівнюють предмети за площею (не називаючи самого слова "площа"). Вони порівнюють не накладанням, а на око.

Наприклад: Листок дуба більший, ніж листок берези. У початкових класах уявлення про площу стають чіткішими: фігури можуть бути різними й однаковими за площею. Дуб Береза

У 4 класі учні ознайомлюються з поняттям площі. Вчитель повідомляє про те, що в розмовах, передачах, по радіо, телебаченню часто можна почути: посівна площа, житлова площа, площа квартири, площа класної кімнати.

Серед предметів, котрі нас оточують, багато таких, поверхня яких має форму трикутника, прямокутника, круга (дно каструлі — круг; підлога, стіни кімнати, класна дошка — прямокутники), кожна з них має площу.

Порівнюючи площі фігур, виставлених на набірному полотні (наприклад: круг, трикутник, квадрат), діти встановлюють, що квадрат займає більше місце, ніж круг або трикутник. Учитель констатує, що в такому разі кажуть, що площа квадрата більша, ніж площа кожної іншої фігури.

Він зазначає, що площа — це величина, яку можна не тільки порівнювати, а й виміряти. Учні порівнюють площі фігур найбільшу площу має прямокутник; площа квадрата більша, ніж площа круга або трикутника; проте порівняти площі трикутника і круга важче. Після цього вчитель ставить завдання (сьогодні на уроці ми будемо вчитися вимірювати площу).

Наприклад: Ввести і закріпити термін „площа геометричних фігур" доцільно за допомогою дидактичного прийому порівняння, поєднавши фронтальну і індивідуальну роботу з учнями. На дошці прикріплюємо паперовий круг і трикутник.

Учитель пояснює, що трикутник — частина круга, отже, його площа менша, ніж площа круга. Закріплюємо уявлення дітей про площу теж на основі аналогічних практичних завдань з використанням набору геометричних фігур, а узагальнюємо вивчене за підручником.

Запитання до учнів: Яка з фігур вміститься всередині іншої? Покажіть це. Діти накладанням таких самих фігур на партах упевнюються, що трикутник вміщується в середині круга. У такому розміщенні їх закріплюємо на дошці: спочатку круг, всередині його — трикутник.

Для порівняння площ добираємо фігури різної форми, щоб запобігти поширеній помилці учнів, які вважають, що площу мають лише прямокутник або квадрат. Важливо уникнути штучного ускладнення викладу нового матеріалу.

На практиці доводилося спостерігати, коли класоводи прагнули дати означення площі („Площа—місце, де стоїть шафа") або ставили запитання: „Що таке площа?" Це — порушення науковості і перевищення програмових вимог щодо навчання молодших школярів. Необхідно пам'ятати, що уявлення про площу формується на інтуїтивно-практичному рівні.

Аналогічно порівнюються за площею і інші фігури, а також предмети, що оточують нас. Але не завжди так легко встановити, яка з двох фігур має більшу (меншу) площу. Вчитель пропонує учням порівняти площі фігур. Виявиться, що жодна з фігур не вміщується в середині іншої. Як же бути?

При виконанні цієї вправи вчитель знайомить учнів ще з одним способом порівняння площ фігур: розбивають кожну фігуру на рівні квадрати і підраховують кількість таких квадратів. Аналогічні вправи на порівняння площ фігур, складених з однакових квадратів виконують за підручником і за кресленнями на дошці. Корисно на цьому уроці розглянути випадок, коли різні за формою фігури мають однакову площу.

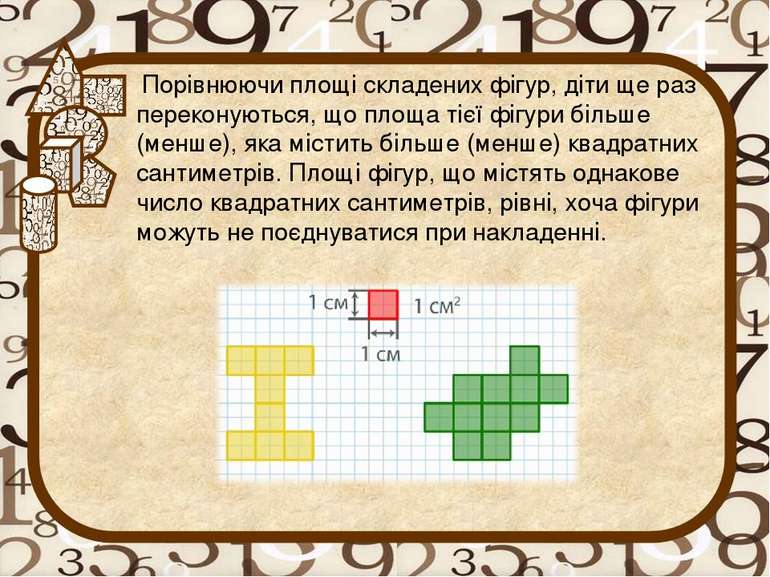
На наступному етапі учнів знайомлять з першої одиницею площі - квадратним сантиметром. Учні креслять у зошитах, вирізають з паперу в клітинку квадрати зі стороною 1 см. Учитель повідомляє: «Це одиниця площі - квадратний сантиметр».  Використовуючи паперові моделі квадратного сантиметра, діти складають з них різні геометричні фігури і знаходять підрахунком їхню площу.

Порівнюючи площі складених фігур, діти ще раз переконуються, що площа тієї фігури більше (менше), яка містить більше (менше) квадратних сантиметрів. Площі фігур, що містять однакове число квадратних сантиметрів, рівні, хоча фігури можуть не поєднуватися при накладенні. 

Надалі наочне уявлення про квадратному сантиметрі і поняття про площу фігур закріплюються. Включаються вправи на знаходження площі фігур, розбитих на квадратні сантиметри. Пропонується при підрахунку квадратних сантиметрів групувати їх по рядах або стовпцях, щоб прискорити знаходження їх загального числа.

На наступному етапі учні знайомляться з прийомом обчислення площі прямокутника (квадрата). Спочатку розглядають прямокутники, які вже розділені на квадратні сантиметри. Їх площа знаходять шляхом підрахунку квадратних сантиметрів в одному ряду, а потім отримане число множать на число рядів.

Наприклад: Якщо в одному ряду 6 кв. см, а таких рядів 5, то площа дорівнює 6-5, тобто 30 кв. см. Дуже важливо при цьому встановити відповідність між довжиною прямокутника і числом квадратних сантиметрів, прилеглих до довжини; шириною прямокутника і числом рядів. Наприклад, якщо в ряду 6 кв. см, то довжина прямокутника 6 см, а якщо рядів 5, то ширина прямокутника 5 см.

Далі вчитель демонструє квадрат зі стороною 4 см і прямокутник зі сторонами З см і 5 см, пропонує порівняти площі цих фігур. Після одержання відповідей учитель повертає фігури, які на зворотному боці поділені на квадрати. Підрахувавши ці квадрати, учні дізнаються, що площа квадрата більша за площу прямокутника.

Окремий урок відводиться для ознайомлення учнів з новими одиницями вимірювання площі. Вводяться відразу всі одиниці вимірювання площі, передбачені програмою. Основу бесіди складає таке повідомлення: "Площа — одна з математичних величин. Для її вимірювання користуються не тільки квадратними сантиметрами, а й іншими одиницями. 

В табл. подано одиниці вимірювання площі, які найчастіше застосовуються в практичній діяльності", 1 мм2 — це площа квадрата, сторона якого 1 мм. 1 см2 — це площа квадрата, сторона якого 1 см. 1 дм2 — це площа квадрата, сторона якого 1 дм. їм2 — це площа квадрата, сторона якого 1 м. Ар — це площа квадрата, сторона якого 10 м. Ар — це сота частина гектара (сотка). Гектар (га) — це площа квадрата, сторона якого 100 м. 1 км2 — це площа квадрата, сторона якого 100 м.

Ознайомивши учнів з квадратним сантиметром, учитель проводить практичну роботу, пов'язану зі знаходженням площі фігур способом розбиття її на квадратні сантиметри. Після цього знаходять площі прямокутників (де лінійні розміри зменшено).

Вимірювання площі за допомогою палетки: Палетка – прозора плівка, поділена на квадрати із стороною 1 см = 10мм.

Для ознайомлення учнів з палеткою як інструментом для вимірювання площі фігур можна скористатися прийомом аналогії. Розкриваючи мету уроку, вчитель повідомляє дітям, що раніше вони знаходили площу фігури тільки прямокутної форми і робили це за правилом. Тепер потрібно навчитись з допомогою особливого пристрою знаходити площу фігур, що мають форму круга, будь-якого многокутника або фігури будь-якої форми.

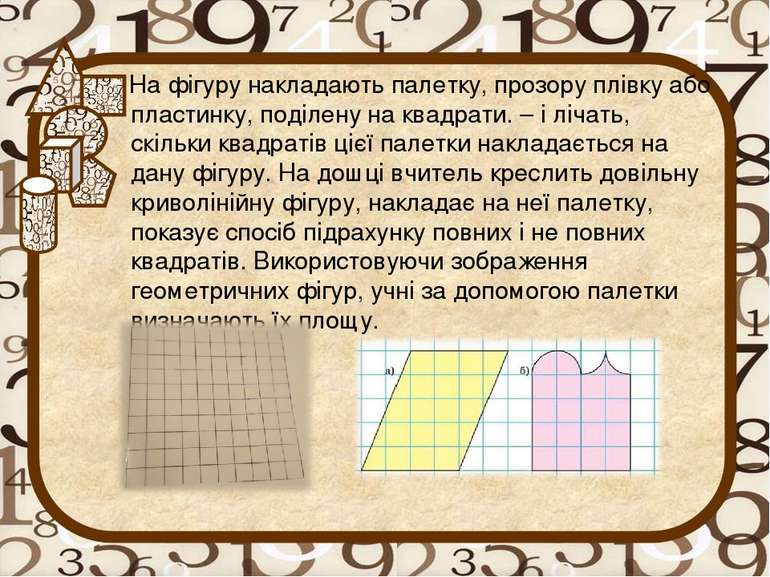
На фігуру накладають палетку, прозору плівку або пластинку, поділену на квадрати. – і лічать, скільки квадратів цієї палетки накладається на дану фігуру. На дошці вчитель креслить довільну криволінійну фігуру, накладає на неї палетку, показує спосіб підрахунку повних і не повних квадратів. Використовуючи зображення геометричних фігур, учні за допомогою палетки визначають їх площу.