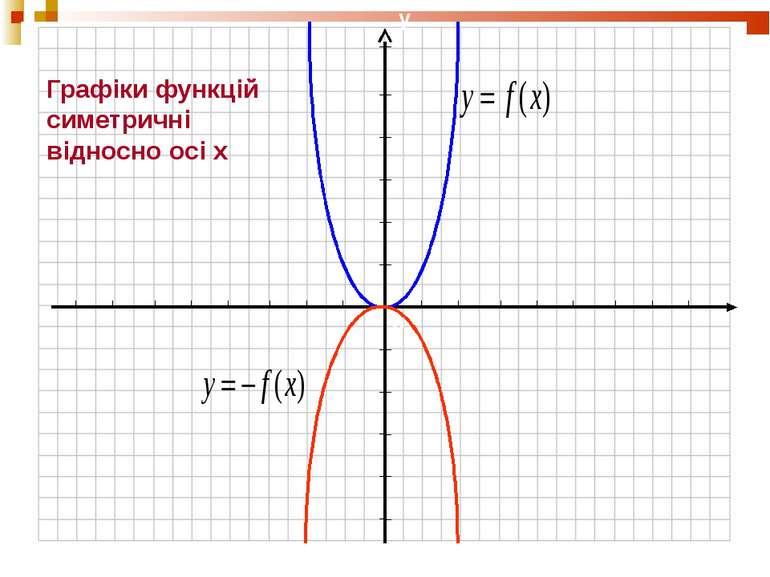
Презентація на тему:
Поняття про найпростіші перетворення графіків функцій

Найпростіші перетворення графіків функцій Кашкаров Д.О. КЗ “ЛСШ І-ІІІ ст. № 21”

«Хіба ти не помітив, що здібний до математики має успіх у всіх науках про природу?» Платон

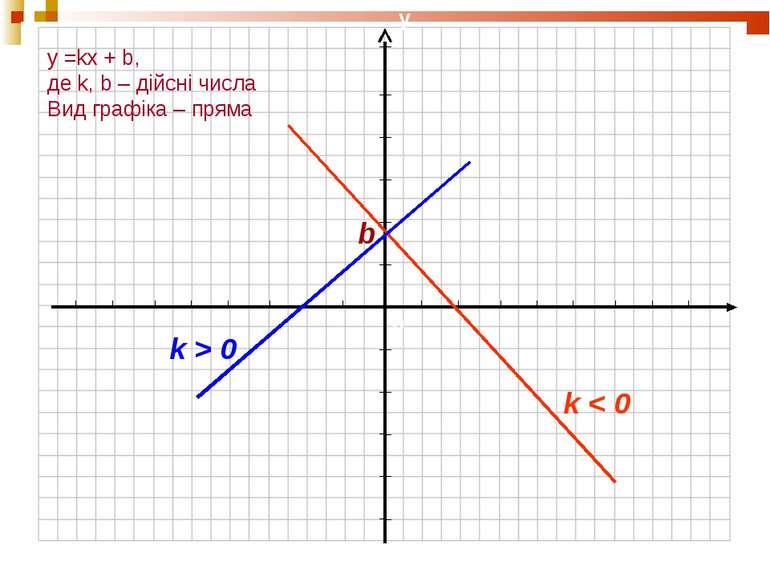
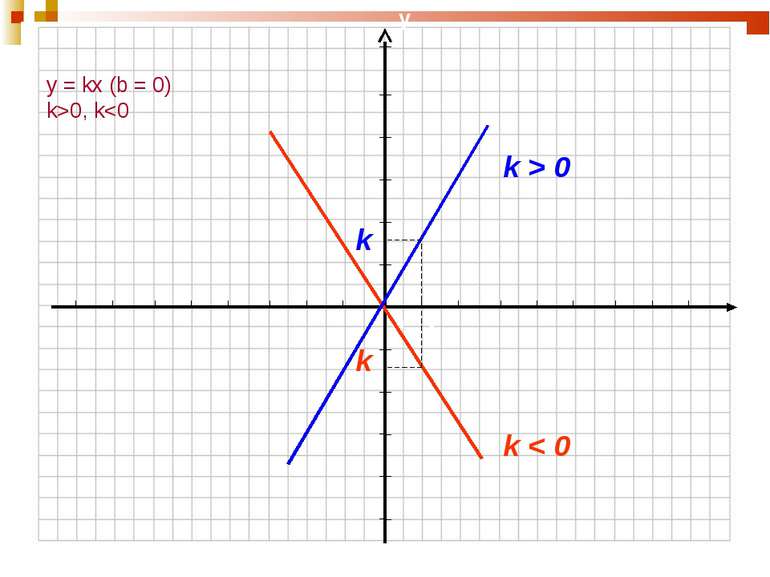
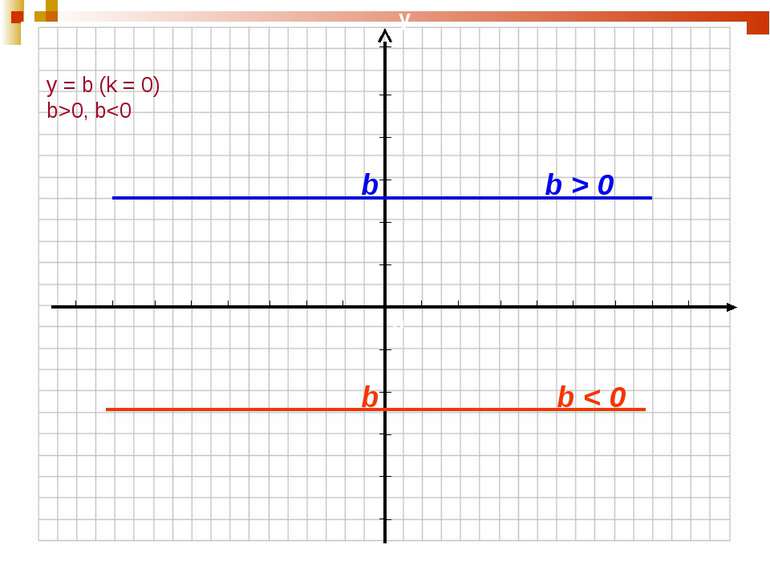
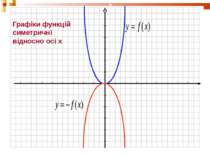
План уроку: Уявлення про перетворення графіків функцій. Розтяг (стиск) графіка функції вздовж осі ординат. Побудова графіків із застосуванням симетрії відносно осі абсцис. Побудова графіків паралельним перенесенням уздовж осі ординат (абсцис).

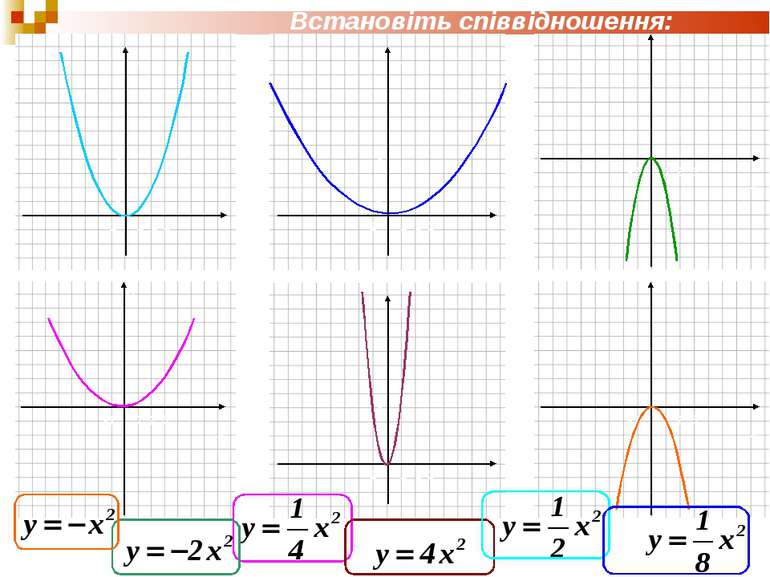
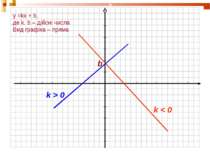
1. Серед наведених функцій укажіть: пряму пропорційність; обернену пропорційність; лінійну функцію, графік якої утворює з віссю абсцис гострий кут.

2. Графіком якої з наведених функцій є горизонтальна пряма: y=8x-7; y=8х; y=8-x; y=8?

3. Областю визначення якої з наведених функції є проміжок (9; +∞):

Рене Декарт (*31 березня 1596 — †11 лютого 1650)

y =kx + b, де k, b – дійсні числа Вид графіка – пряма k < 0 k > 0 b

y = kx (b = 0) k>0, k 0 k k 1

y = b (k = 0) b>0, b 0 b b < 0

Графіки функцій симетричні відносно осі х

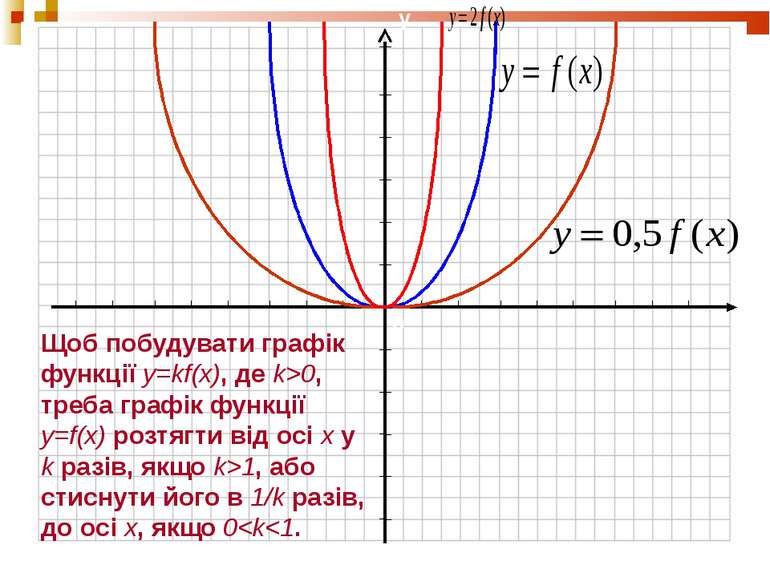
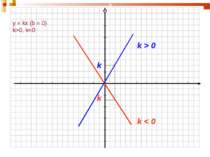
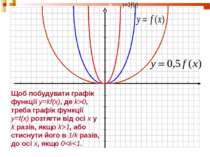
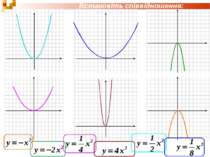
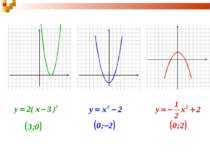
Щоб побудувати графік функції y=kf(x), де k>0, треба графік функції y=f(x) розтягти від осі х у k разів, якщо k>1, або стиснути його в 1/k разів, до осі х, якщо 0

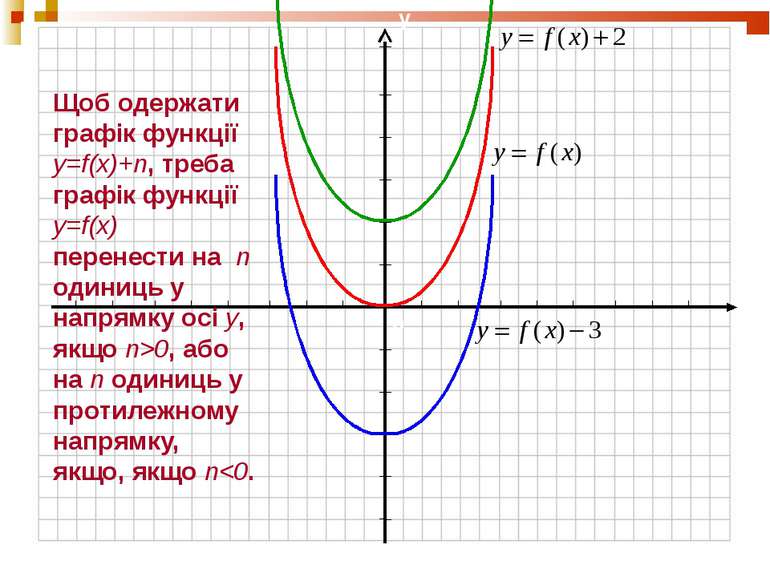
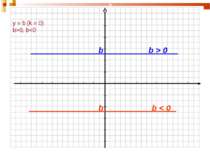
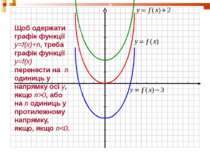
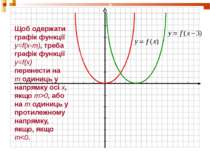
Щоб одержати графік функції y=f(x)+n, треба графік функції y=f(x) перенести на n одиниць у напрямку осі y, якщо n>0, або на n одиниць у протилежному напрямку, якщо, якщо n

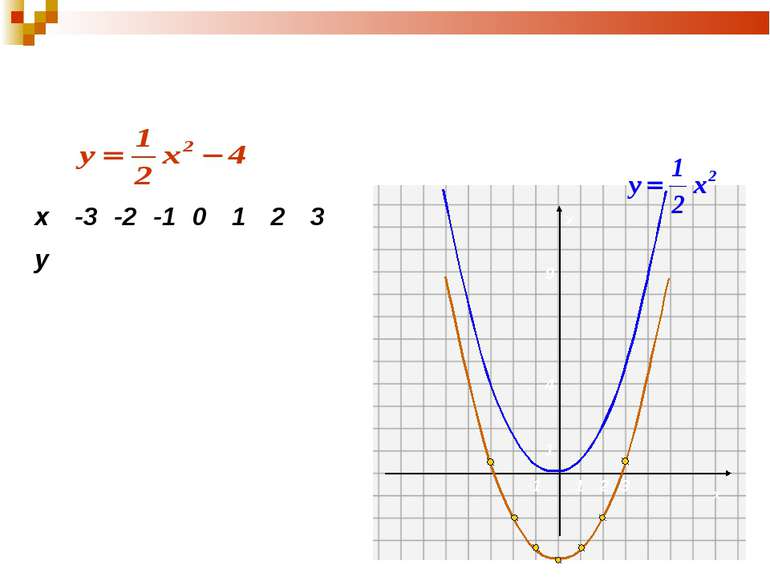
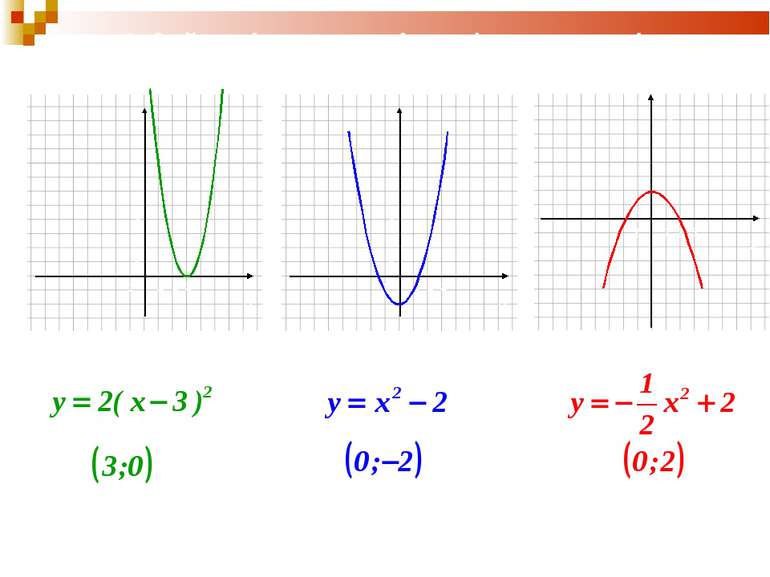
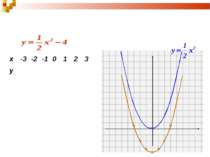
1. Побудуємо графік функції виду: у=kх2+n 0,5 -2 -3,5 -4 -3,5 -2 0,5 Порівняємо його з графіком вихідної функції та зробимо висновки. х -3 -2 -1 0 1 2 3 у

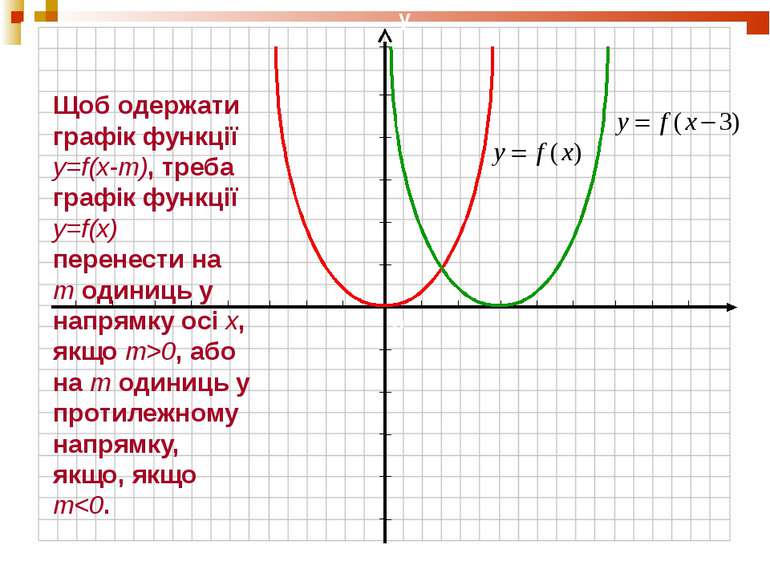
Щоб одержати графік функції y=f(x-m), треба графік функції y=f(x) перенести на m одиниць у напрямку осі x, якщо m>0, або на m одиниць у протилежному напрямку, якщо, якщо m

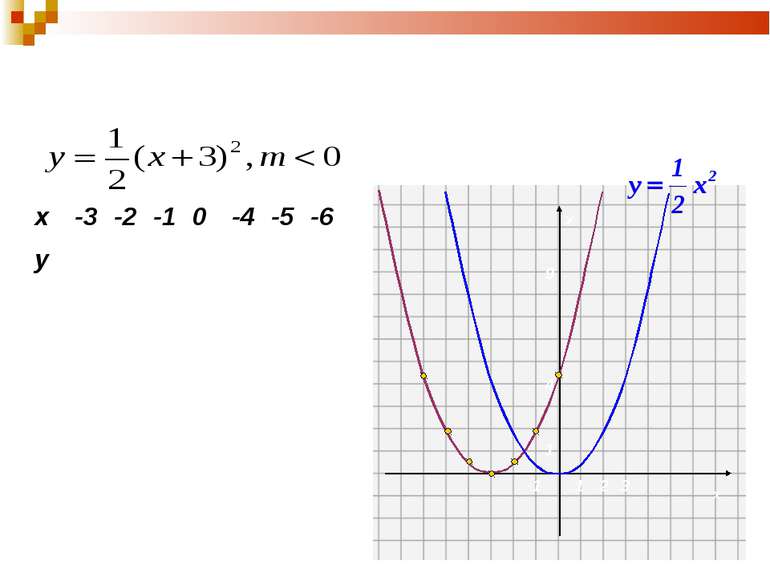
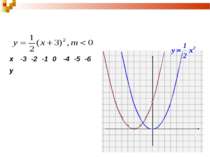
2. Побудуємо графік функції виду у=k(х-m)2 0 0,5 2 4,5 0,5 2 4,5 Порівняємо його з графіком вихідної функції та зробимо висновки. х -3 -2 -1 0 -4 -5 -6 у

У Встановіть співвідношення:

Задайте формулою функцію, якщо вихідна функція у=х2

Розкажіть, за допомогою яких перетворень можна дістати із графіка функції у = х2 графік функції: 1) у=х2-1; 2) у=х2+1; 3) у=(х+1)2; 4) у=(х-1)2; 5) у=(х+1)2-1?

У Задайте формулою функцію та запишіть координати вершини параболи:

Домашнє завдання: Вивчити § 10 (ст. 91-96). Повторити теоретичний матеріал за конспектом. Розв'язати вправи № 408, 411, 412.