Презентація на тему:
ПЛАНУВАННЯ ТА ОБРОБКА РЕЗУЛЬТАТІВ ОДНОФАКТОРНИХ ЕКСПЕРИМЕНТІВ З МОДЕЛЯМИ
Завантажити презентацію
ПЛАНУВАННЯ ТА ОБРОБКА РЕЗУЛЬТАТІВ ОДНОФАКТОРНИХ ЕКСПЕРИМЕНТІВ З МОДЕЛЯМИ
Завантажити презентаціюПрезентація по слайдам:
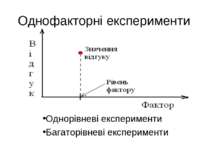
План лекції Однофакторні експерименти на одному рівні. Довірчий інтервал. Планування багаторівневих однофакторних експериментів. Дисперсійний аналіз результатів експериментів. Регресійний аналіз результатів експериментів. Компоненти фреймворку Simulation для побудови моделі СМО.
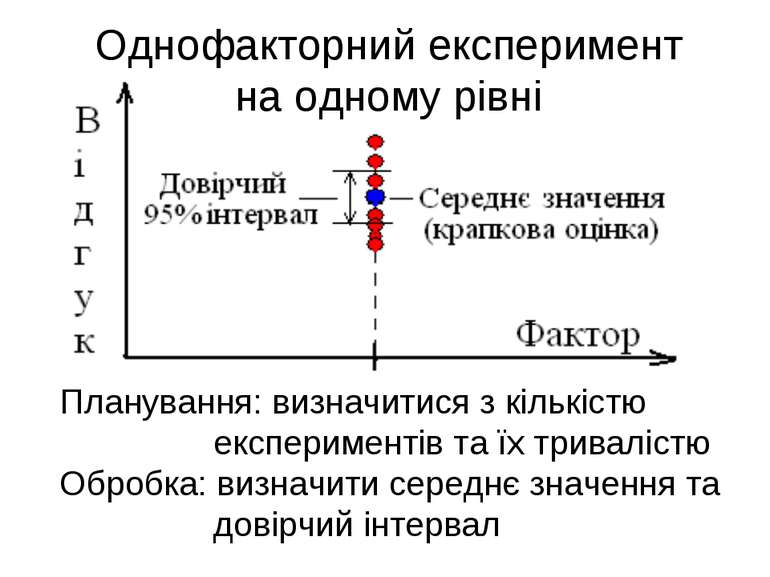
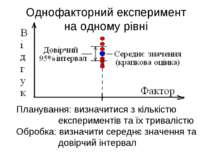
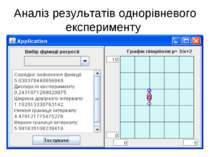
Однофакторний експеримент на одному рівні Планування: визначитися з кількістю експериментів та їх тривалістю Обробка: визначити середнє значення та довірчий інтервал
Значення коефіцієнту tγ Якщо вибірка велика, використовуємо функцію Лапласа Для імовірності γ = 0.99, tγ = 2.57 Для імовірності γ = 0.95, tγ = 1.96 Якщо вибірка мала, використовуємо розподіл Стьюдента Для надійності95% якщо обсяг вибірки 30, tγ дорівнює 2.05 якщо обсяг вибірки 10, tγ дорівнює 2.23.
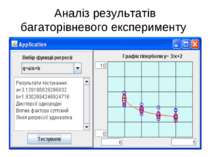
Однофакторний експеримент на багатьох рівнях Планування: - скільки рівнів потрібно? - скільки експериментів на рівні? Обробка: - знайти дисперсію експерименту - визначити чи впливає фактор - підібрати рівняння регресії - перевірити рівняння на адекватність
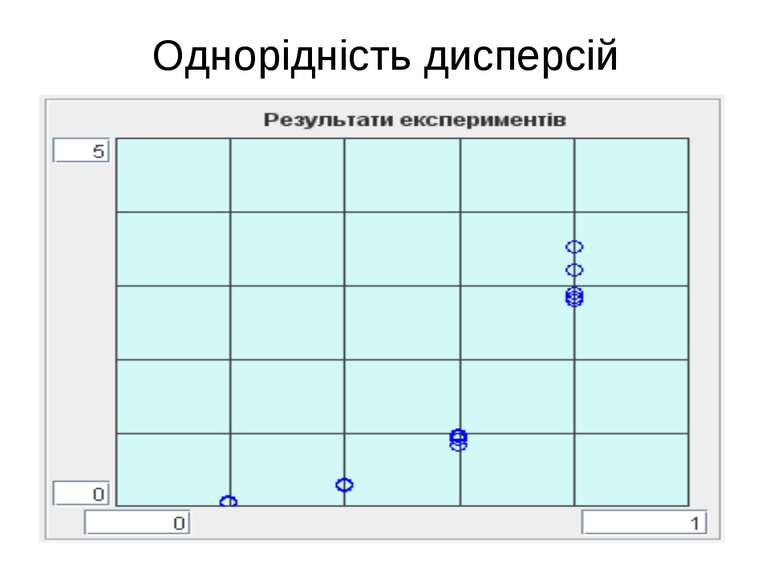
Критерій Кочрена Отримане значення відношення порівнюють із критичним значенням, яке можна знайти в статистичних таблицях розподілення Кочрена по: - кількості степенів свободи для оцінюваних дисперсій, яке дорівнює n-1 (n – кількість дослідів на рівні), - кількості порівнюваних дисперсій – p, - прийнятому рівневі значимості. Наприклад, при рівні значимості 0.05, кількості рівнів 4 і кількості експериментів на рівні 10 отримуємо критичне значення 0.5.
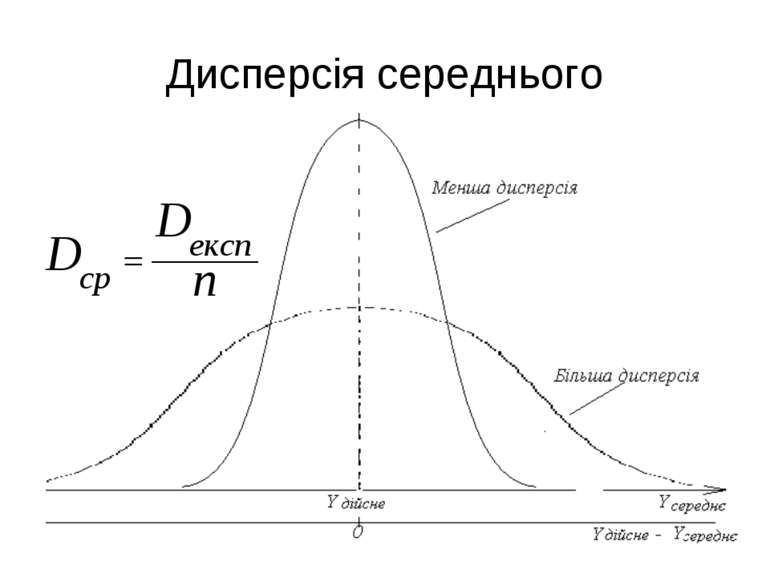
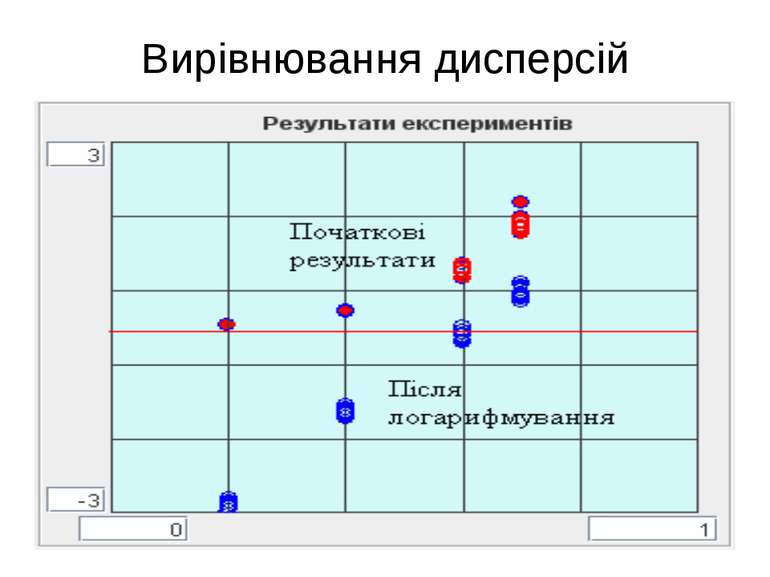
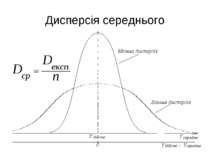
Дисперсія експерименту Якщо дисперсії однорідні, то в якості оцінки точності експериментів, які проводяться, приймають середнє значення дисперсій на рівнях.
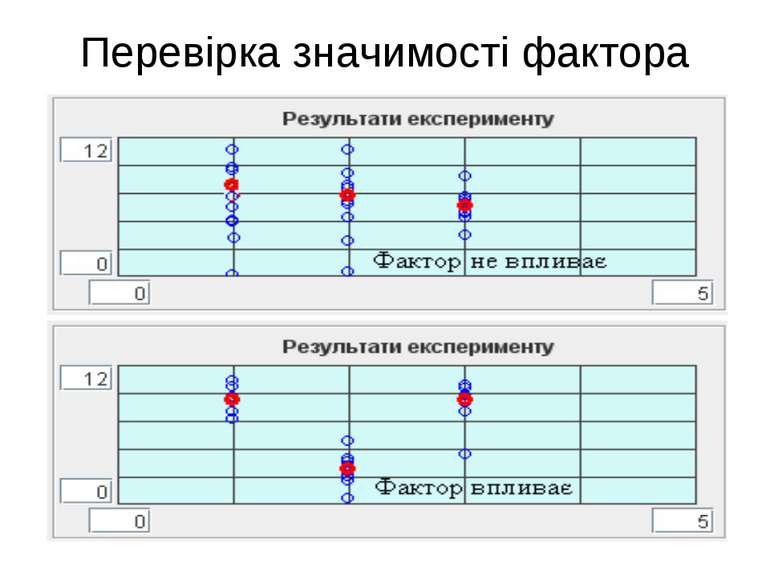
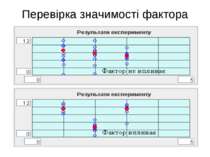
Перевірка значимості фактору Дисперсійний аналіз значимості фактору полягає у порівнянні відхилень: - пов'язаних із змінами фактору; - викликаних похибками експерименту.
Перевірка значимості фактору Якщо дисперсія фактора менше дисперсії середніх значень, то впливу фактору на відгук нема. Вплив фактора є суттєвим у тому випадку, якщо дисперсія фактора набагато більше дисперсії середніх значень відгуку
Критерій Фішера Отримане значення відношення порівнюють із критичним значенням критерію Фішера , яке можна знайти в статистичних таблицях по: - кількості степенів свободи для дисперсії фактору, яке дорівнює р -1, де р – кількість рівнів; - кількості степенів свободи для дисперсії середніх, яке дорівнює p*(n-1), де n – кількість дослідів на рівні; - прийнятому рівневі значимості. Наприклад, при рівні значимості 0.05, кількості рівнів 3 і кількості експериментів на рівні 10 отримуємо критичне значення 3.3.
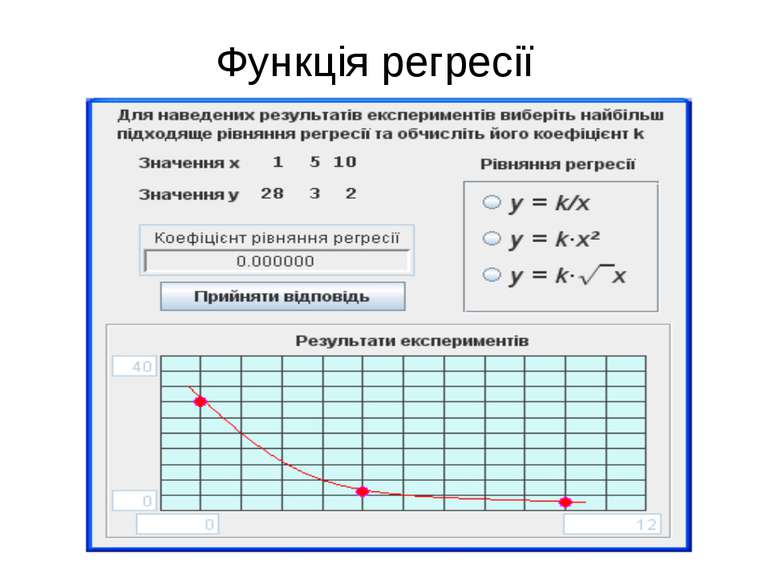
Функція регресії y(x )= a1·φ1(x)+ a2·φ2(x)+...+ an·φn(x) Зручніше всього функцію регресії представляти у вигляді лінійної комбінації елементарних функцій, які залежать від величини фактора У наведеній залежності невідомими є коефіцієнти a1, a2 ,… an. Такий вигляд функції спрощує аналітичне дослідження
Метод найменших квадратів В якості критерію близькості лінії регресії до результатів експерименту приймають суму квадратів відхилень експериментальних точок від відповідних значень лінії регресії Найкращими значеннями коефіцієнтів а1, а2,…вважаються такі, при яких сума квадратів відхилень буде мінімальною.
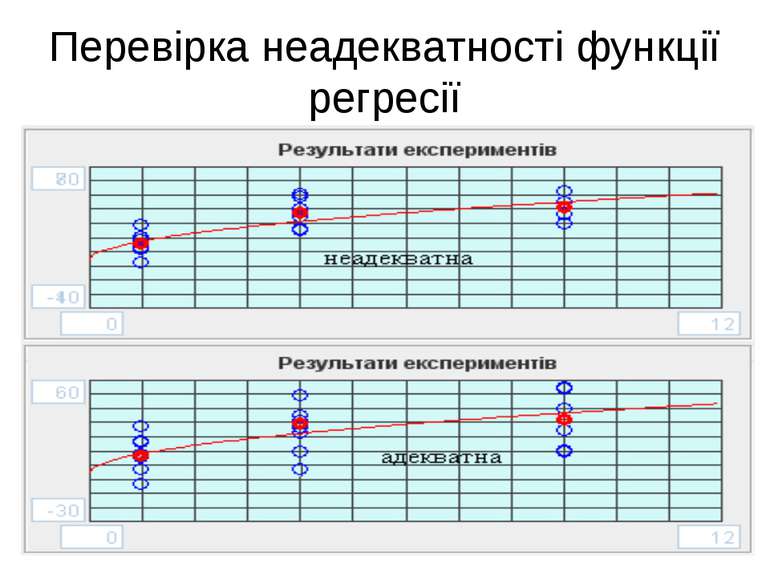
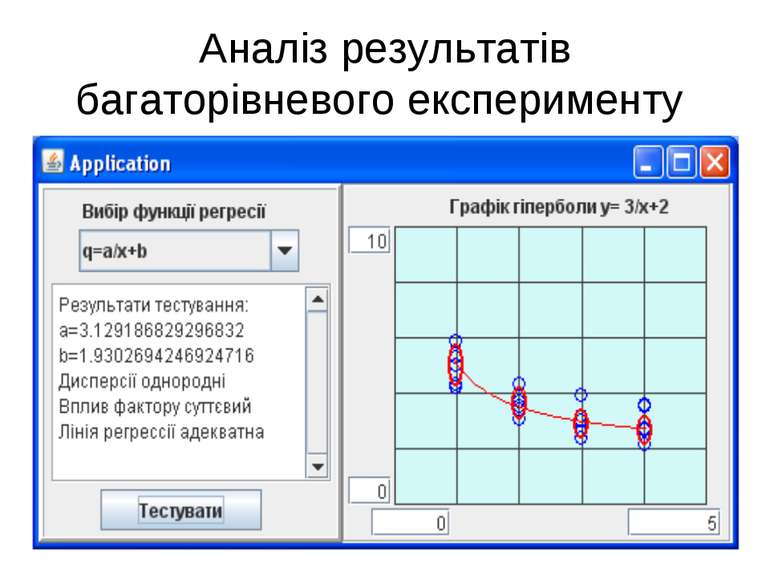
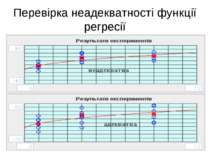
Перевірка неадекватності Дисперсійний аналіз неадекватності полягає у порівнянні : - відхилень лінії регресії від середніх значень відгуку; - відхилень пов'язаних із похибками експерименту.
Перевірка неадекватності Якщо дисперсія неадекватності менше дисперсії середніх значень, то лінію регресії можна вважати адекватно Лінію регресії вважають неадекватною у тому випадку, коли дисперсія неадекватності набагато більше дисперсії середніх значень функції відгуку
Критерій Фішера Отримане значення відношення порівнюють із критичним значенням критерію Фішера , яке можна знайти в статистичних таблицях по: - кількості степенів свободи для дисперсії неадекватності, що дорівнює р - k, де р – кількість рівнів, k - кількість коефіцієнтів функції регресії; - кількості степенів свободи для дисперсії середніх, яке дорівнює p*(n-1), де n – кількість дослідів на рівні; - прийнятому рівневі значимості. Наприклад, при рівні значимості 0.05, кількості рівнів 3 і кількості експериментів на рівні 10, для k=1 отримуємо критичне значення 3.1.
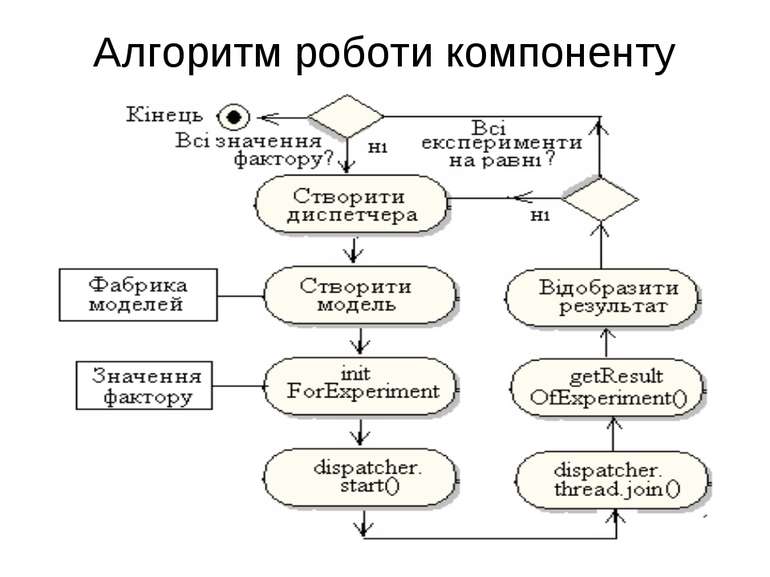
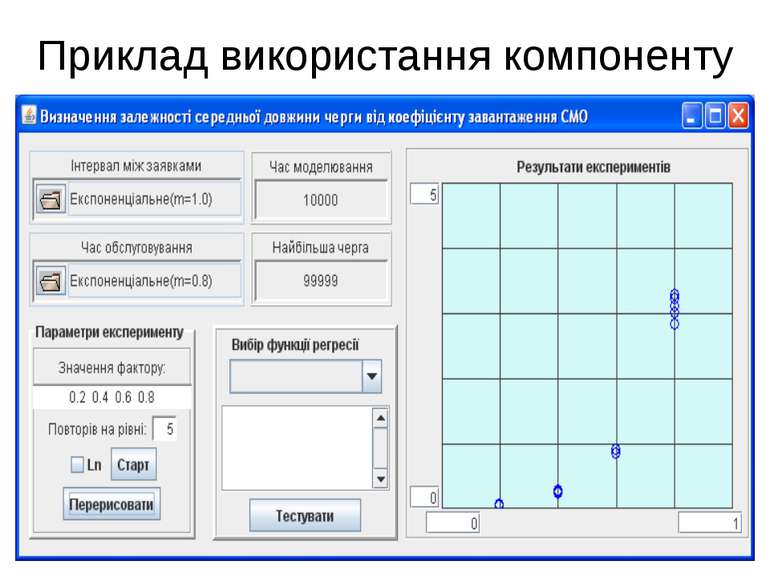
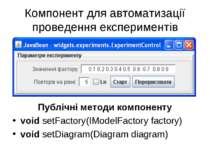
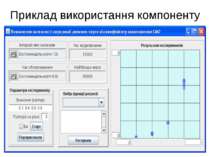
Компонент для автоматизації проведення експериментів Публічні методи компоненту void setFactory(IModelFactory factory) void setDiagram(Diagram diagram)
Інтерфейси для компоненту public interface IModelFactory { public Object createModel(Dispatcher dispatcher); } public interface IExperimentable { public void initForExperiment(double factor); public double getResultOfExperiment(); }
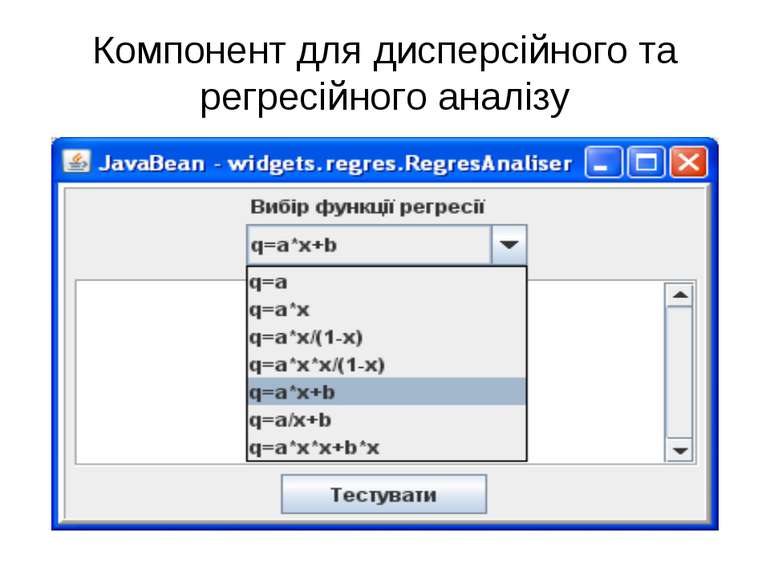
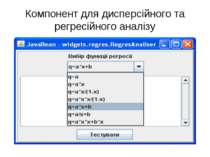
Налаштування компоненту Інтерфейс для звязку із джерелом даних public interface IRegresable { public double[] getFactorsArray(); public double[][] getResultMatrix(); } Методи ініціалізації компоненту public void setIRegresable(IRegresable r) public void setDiagram(Diagram d) public void addFunction(RegresTesters t)
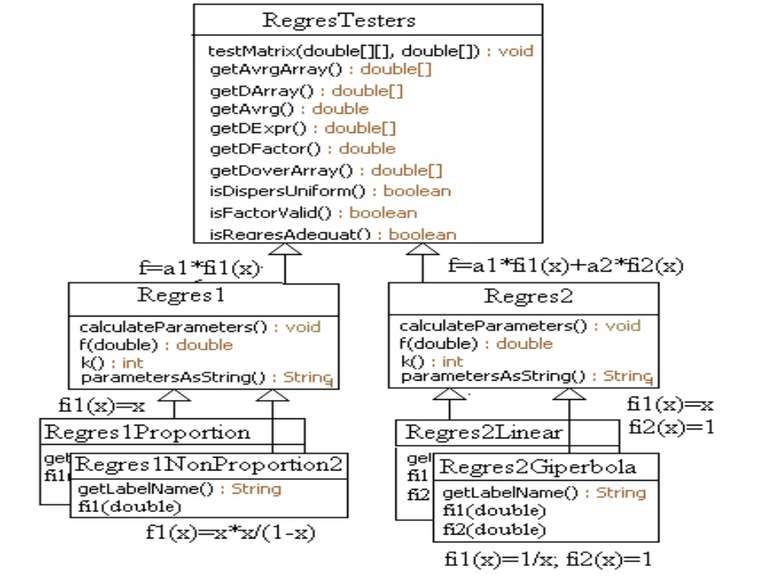
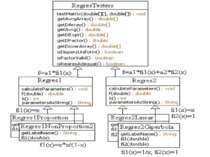
Реалізація спадкоємця класу Regres1 public class Regres1Parabola extends Regres1 { public String getLabelName() { return "q=a*x*x"; } public double fi1(double x) { return x*x; } }
Реалізація спадкоємця класу Regres2 public class Regres2Giperbola extends Regres2 { public String getLabelName() { return "q=a/x+b"; } public double fi1(double x) { return 1/x; } public double fi2(double x) { return 1; } }
Схожі презентації
Категорії