Презентація на тему:
Основні поняття математичної логіки

Основні поняття математичної логіки

Висловлення. Логічні константи. Логічні операції Логіка (грец. λόγος – слово, смисл, думка, мова) – наука про форми, методи і закони інтелектуальної пізнавальної діяльності, правильного мислення, про способи міркування. Логіка як наука вивчає способи отримання правильних висновків з висновків, отриманих раніше.

Математична логіка Математична логіка - є наука про закони математичного мислення. Основне поняття математичної логіки: Висловлення розповідне речення, про яке можна однозначно сказати, правильне (істинне) воно чи неправильне (хибне). Основна властивість висловлення істинність. Значення істинності висловлення позначають 1 або true, якщо висловлення істинне, 0 або false, якщо висловлення хибне Значення true і false називають логічними константами

Математична логіка Із заданих висловлень можна отримати нові – складені, – використовуючи логічні операції: заперечення, кон’юнкцію (лат. conjunctio – об’єднання), диз’юнкцію (лат. disjunctio – роз’єднання) та ін. Дайте відповідь: А = «Існує найменше просте число », тоді - Просте число

Математичка логіка

Математичка логіка

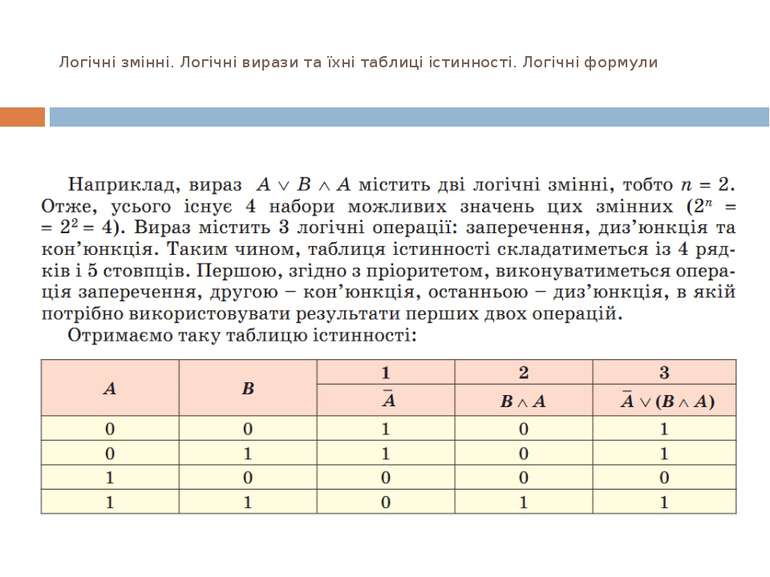
Логічні змінні. Логічні вирази та їхні таб лиці істинності. Логічні формули Алгеброю логіки (булевою логікою, алгеброю висловлень) називають розділ математичної логіки, в якому розглядаються загальні властивості виразів, складених з висловлень з використанням логічних операцій. Для логічних операцій, розглянутих вище, визначено такий пріоритет операцій: заперечення, кон’юнкція, диз’юнкція. Для змінення цього порядку виконання логічних операцій використовують дужки.

Логічні змінні. Логічні вирази та їхні таблиці істинності. Логічні формули Для обчислення значення істинності логічного виразу можна викоистати таб лиці істинності. Для складання та заповнення таб лиці істинності потрібно: 1. Обчислити кількість можливих наборів значень логічних змінних. Якщо формула містить n різних логічних змінних, то можливих наборів значень цих змінних буде 2n. Це число визначає кількість рядків у таблиці істинності. 2. Обчислити кількість логічних операцій у логічному виразі. Ця кількість плюс кількість логічних змінних визначає кількість стовпців таблиці. 3. Заповнити перші n стовпців усіма можливими наборами значень логічних змінних. 4. Заповнити кожний наступний стовпець значеннями, отриманими під час виконання чергової логічної операції. Черговість встановлюється згідно з названим пріоритетом операцій.

Логічні змінні. Логічні вирази та їхні таблиці істинності. Логічні формули

Логічні змінні. Логічні вирази та їхні таблиці істинності. Логічні формули

Перевір себе