Презентація на тему:
Квадратична функція

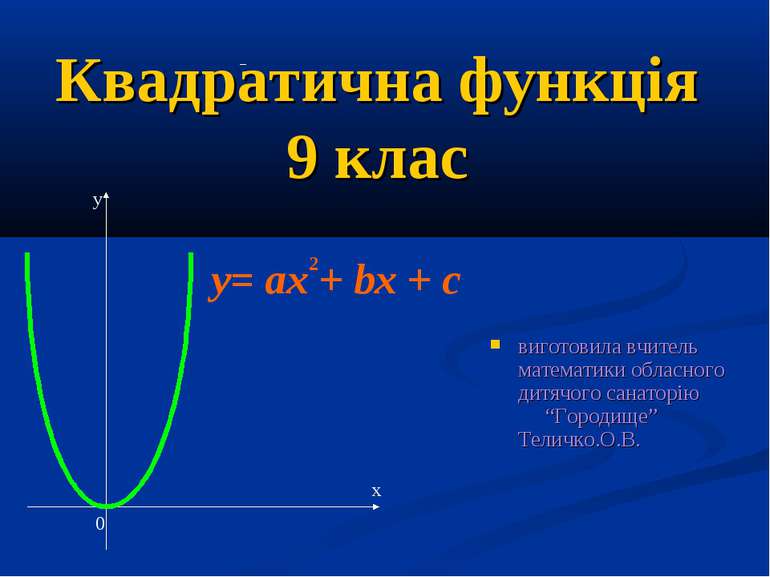
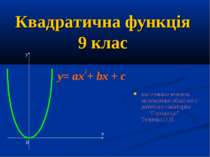
Квадратична функція 9 клас виготовила вчитель математики обласного дитячого санаторію “Городище” Теличко.О.В. у х 0 y= ax + bx + c 2

Вивчаючи тему, ми повинні навчитися : розпізнавати квадратичну функцію ; знаходити координати вершини та нулі функції ; визначати напрям віток графіка функції ; виконувати побудову графіка квадратичної функції ; вміти досліджувати властивості квадратичної функції .

Означення квадратичної функції Квадратичною функцією називається функція виду y=ax +bx+c , де х - незалежна змінна, а=0. 2 /

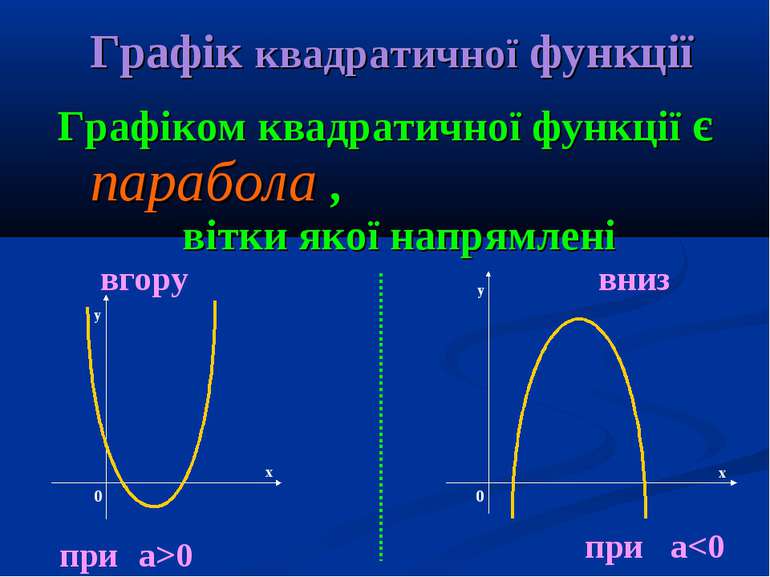
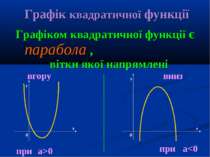
Графік квадратичної функції Графіком квадратичної функції є парабола , вітки якої напрямлені вгору при a>0 вниз при a

Координати вершини параболи: x = - , y = y(x )= , де D = b – 4ac. Рівняння осі симетрії параболи: y = x b 2a b b D 4a b b -

Алгоритм побудови графіка квадратичної функції y=ax +bx+c для прикладу побудуємо графік функції у=х - 4х +3 1. Побудуємо вершину параболи. Обчислимо координату вершини графіка функції у=х - 4х+3, та побудуємо її: x = х = =2 y = у = 2 – 4*2 +3=-1 2 2 2 b 0 b 2a -b +4ac 2 4a -4 2*1 х у 0 (2;-1)-вершина параболи 2 b

2. Знайдемо координати точки перетину параболи з осями координат , тобто знайдемо нулі функції : а) з віссю абсцис: для цього розвяжемо рівняння ax +bx+c = 0 Зауваження. Парабола може не перетинати осі абсцис. х -4х+3=0 ; х =3 , х =1. Отже (3;0) ,(1;0) – точки перетину параболи з Ох б) з віссю ординат: х = 0 , у = с Тобто х=0 , у=0 -4*0+3=3 (0;3) – точка перетину параболи з віссю Оу , 2

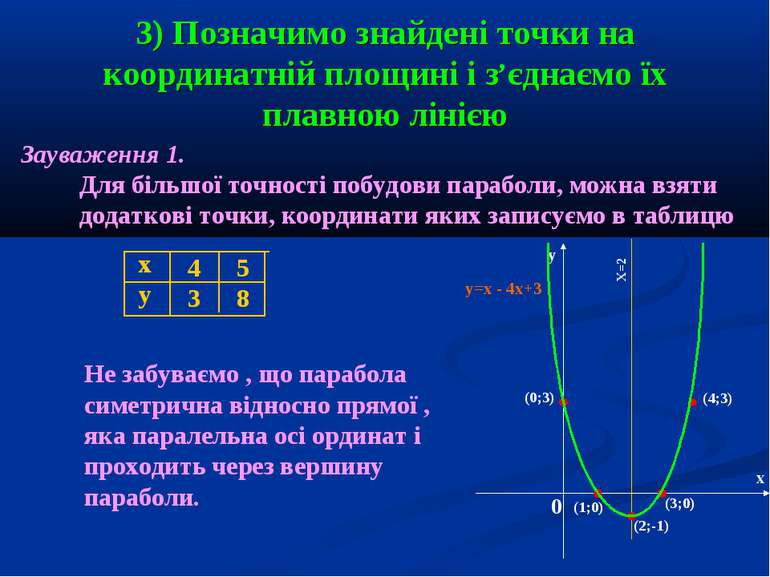
3) Позначимо знайдені точки на координатній площині і з єднаємо їх плавною лінією Зауваження 1. Для більшої точності побудови параболи, можна взяти додаткові точки, координати яких записуємо в таблицю х у 4 5 3 8 Не забуваємо , що парабола симетрична відносно прямої , яка паралельна осі ординат і проходить через вершину параболи. у х 0 (0;3) (4;3) (1;0) (2;-1) (3;0) Х=2 у=х - 4х+3 ,

Зауваження 2. Графіки квадратичних функцій у = ах , у = а(х-m) +n , y = ax +n можна побудувати , виконавши відповідні геометричні перетворення графіка функції у = х 2 2 2 2

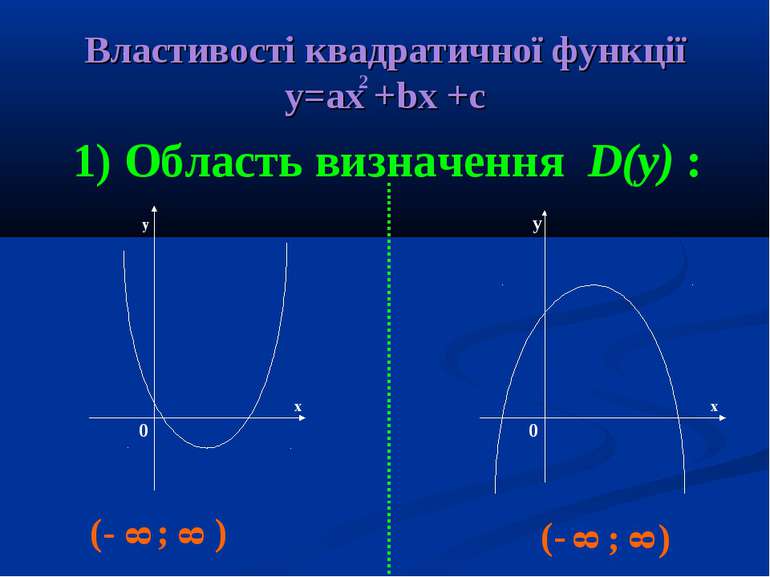
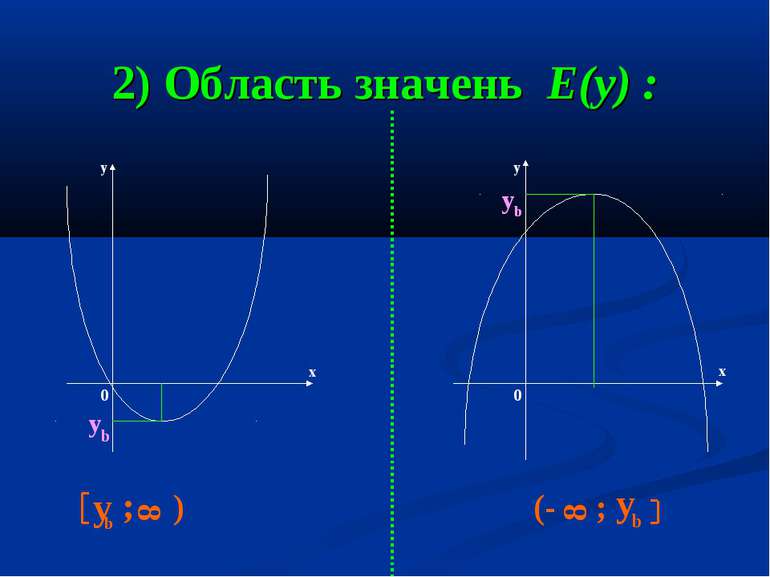
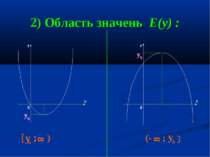
Властивості квадратичної функції у=ах +bx +c 1) Область визначення D(y) : y y x x 0 0 (- 8 ; 8 ) 8 (- ; 8 ) 2

2) Область значень Е(у) : у у х х у b y b y b ; 8 ) (- 8 ; у b 0 0

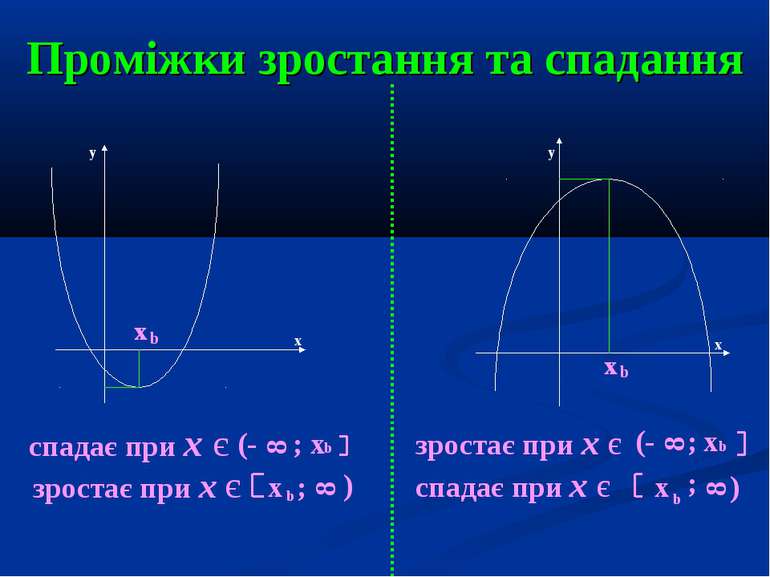
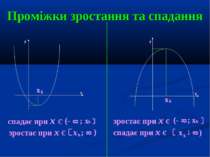
Проміжки зростання та спадання x x b b y y x x спадає при х є (- 8 ; х b зростає при х є x b ; 8 ) зростає при х є спадає при х є (- 8 ; х b x b ; 8 )

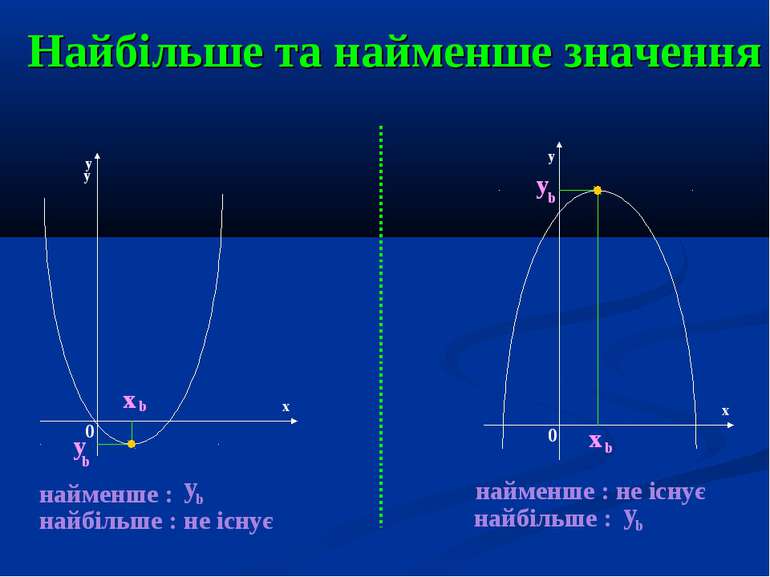
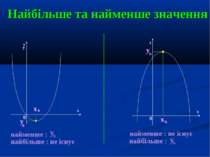
Найбільше та найменше значення y y y x x 0 0 y b x b y b x b найменше : найбільше : не існує y b найменше : не існує найбільше : y b

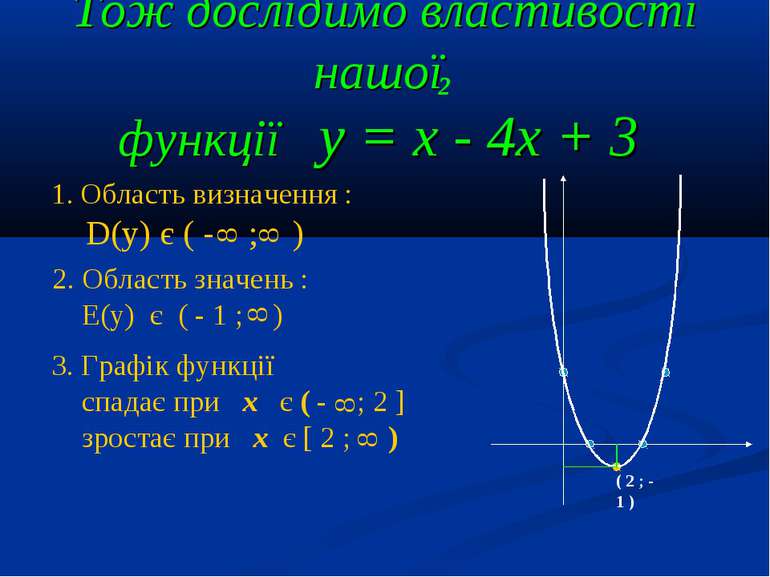
Тож дослідимо властивості нашої функції y = x - 4x + 3 2 ( 2 ; - 1 ) Область визначення : D(у) є ( - ; ) 8 8 2. Область значень : Е(у) є ( - 1 ; ) 8 3. Графік функції спадає при x є ( - ; 2 ] зростає при x є [ 2 ; ) 8 8

А тепер перевіримо на скільки добре ви засвоїли даний матеріал

Математичний диктант 1) Квадратичною функцією називається функція , яку можна задати формулою ...

2) Графіком квадратичної функції є... 3) Графік квадратичної функції у = ах + bx + c симетричний відносно прямої... 2

4) Вітки параболи напрямленні вгору , якщо ... 5) Абсцису вершини параболи можна знайти за формулою ...

6) Значення Х , при яких значення функції дорівнює нулю , називаються ...

7) Область визначення параболи - ... 8) Оласть значень : якщо а > 0 , то ... ; якщо a < 0 , то ... .

Молодці всі ті , хто добре справився із даним завданням .

Отже , вивчиши даний матеріал , ви вмієте : * розпізнавати квадратичну функцію ; * знаходити координати вершини параболи та нулі функції ; * визначати напрямок віток графіка функції ; * будувати графік квадратичної функції ; * досліджувати властивості квадратичної функції .

Дякую за співпрацю і до зустрічі