Презентація на тему:
Квадратична функція 9 клас

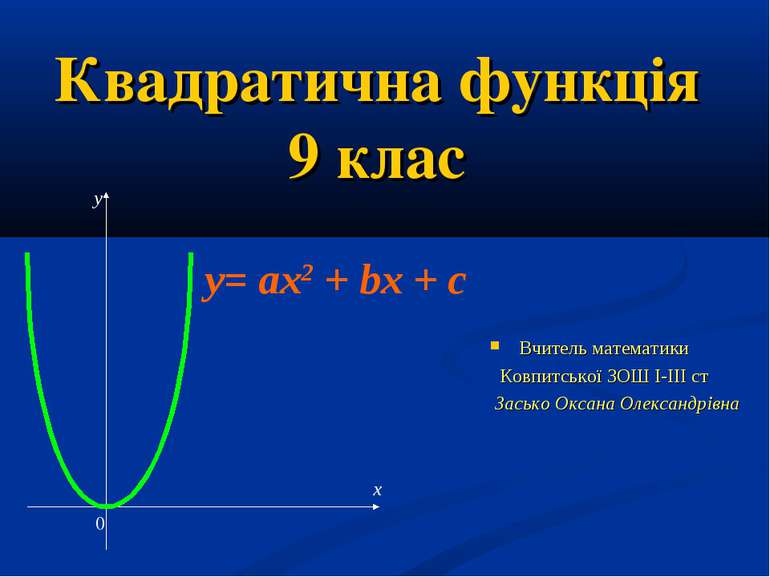
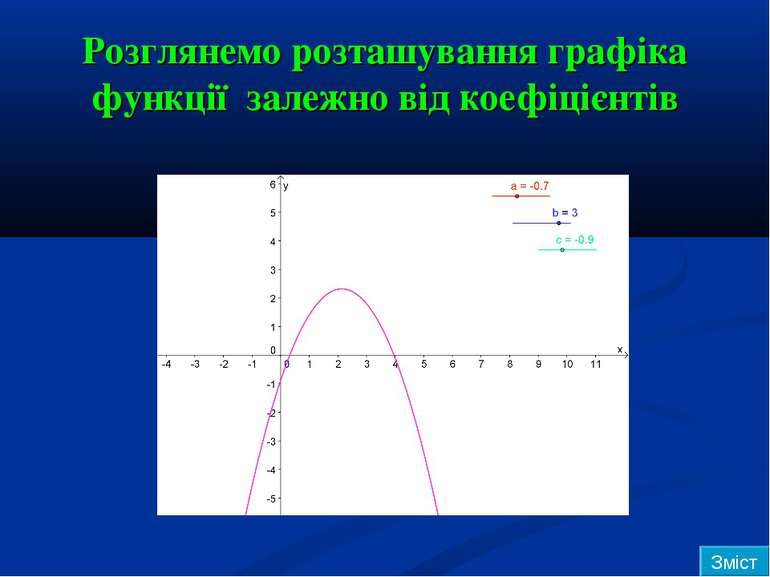
Квадратична функція 9 клас Вчитель математики Ковпитської ЗОШ І-ІІІ ст Засько Оксана Олександрівна y x 0 y= ax2 + bx + c

Вивчаючи тему, ми повинні навчитися : розпізнавати квадратичну функцію ; знаходити координати вершини та нулі функції ; визначати напрям віток графіка функції ; виконувати побудову графіка квадратичної функції ; вміти досліджувати властивості квадратичної функції .

Зміст Означення квадратичної функції. Графік квадратичної функції. Алгоритм побудови графіка. Властивості квадратичної функції. Практичні вправи.

Означення квадратичної функції Квадратичною функцією називається функція виду y=ax2+bx+c, де х - незалежна змінна, а=0, a, b, c – деякі числа / Зміст

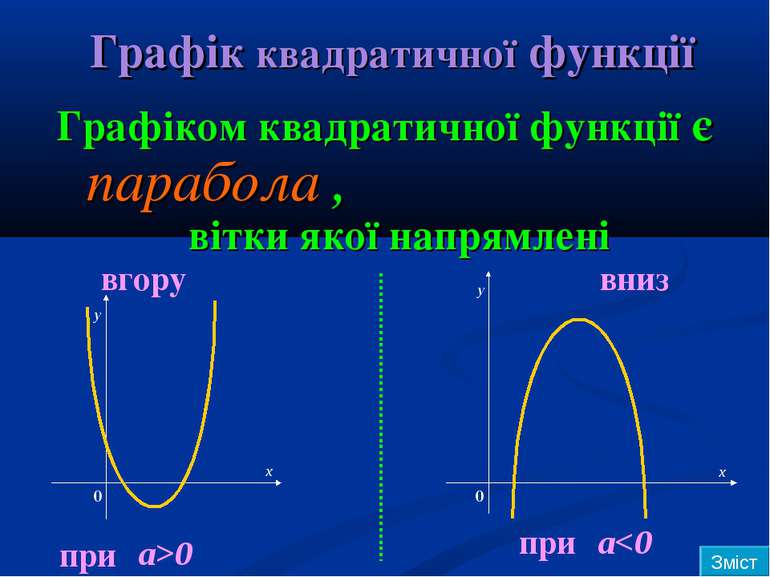
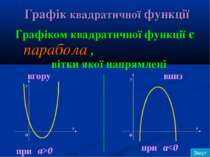
Графік квадратичної функції Графіком квадратичної функції є парабола , вітки якої напрямлені вгору при a>0 вниз при a

Координати вершини параболи: xb= - , yb = y(xb)= , де D = b2 – 4ac. Рівняння осі симетрії параболи: y = x b 2a D 4a b - Зміст

Розглянемо розташування графіка функції залежно від коефіцієнтів Зміст

Алгоритм побудови графіка квадратичної функції y=ax2+bx+c для прикладу побудуємо графік функції у=х2 - 4х +3 1. Побудуємо вершину параболи. Обчислимо координату вершини графіка функції у=х2 - 4х+3, та побудуємо її: xb= х = =2 y = у = 22 – 4·2 +3=-1 b b 2a -(b -4ac) 2 4a -4 2·1 х у 0 (2;-1)-вершина параболи Зміст

2. Знайдемо координати точки перетину параболи з осями координат , тобто знайдемо нулі функції : а) з віссю абсцис: для цього розвяжемо рівняння ax +bx+c = 0 Зауваження. Парабола може не перетинати осі абсцис. х2 -4х+3=0 ; х =3 , х =1. Отже (3;0) ,(1;0) – точки перетину параболи з Ох б) з віссю ординат: х = 0 , у = с Тобто х=0 , у=0 -4·0+3=3 (0;3) – точка перетину параболи з віссю Оу , 2 Зміст

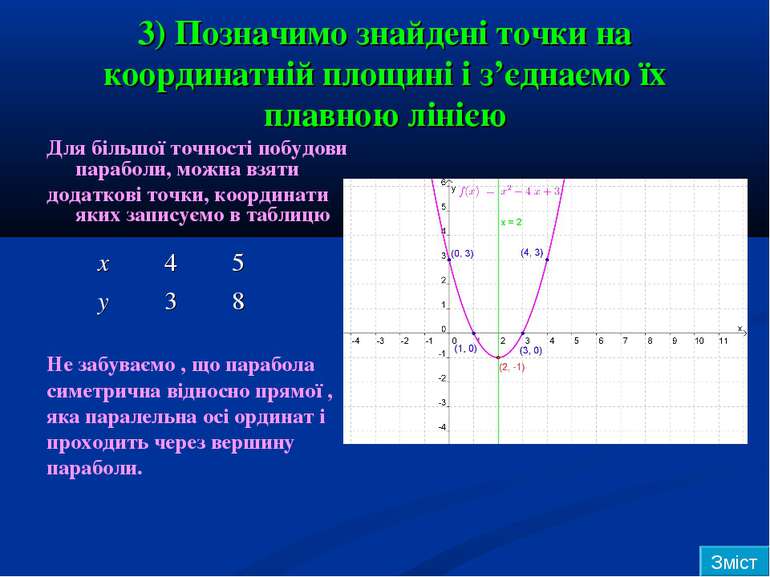
3) Позначимо знайдені точки на координатній площині і з’єднаємо їх плавною лінією Для більшої точності побудови параболи, можна взяти додаткові точки, координати яких записуємо в таблицю Не забуваємо , що парабола симетрична відносно прямої , яка паралельна осі ординат і проходить через вершину параболи. Зміст x 4 5 y 3 8

Зауваження 2. Графіки квадратичних функцій у = ах2, у = а(х-m)2+n , y = ax2+n можна побудувати , виконавши відповідні геометричні перетворення графіка функції у = х2 Зміст

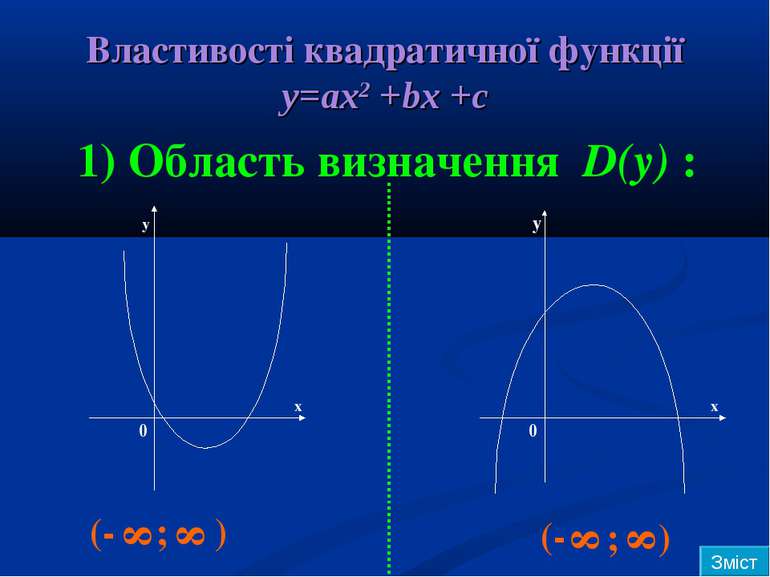
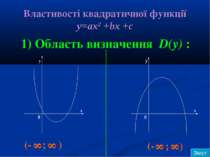
Властивості квадратичної функції у=ах2 +bx +c 1) Область визначення D(y) : y y x x 0 0 (- 8 ; 8 ) 8 (- ; 8 ) Зміст

2) Область значень Е(у) : у у х х у b y b y b ; 8 ) (- 8 ; у b 0 0 Зміст

Проміжки зростання та спадання x x b b y y x x спадає при х є (-∞; хb] зростає при х є [xb; +∞) зростає при х є (-∞; хb] спадає при х є [xb; +∞) Зміст

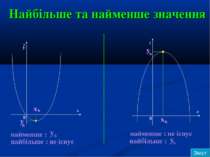
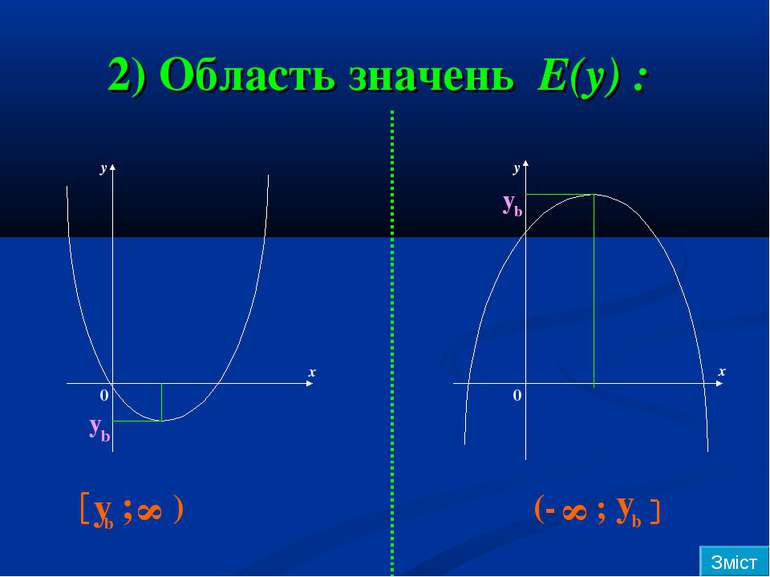
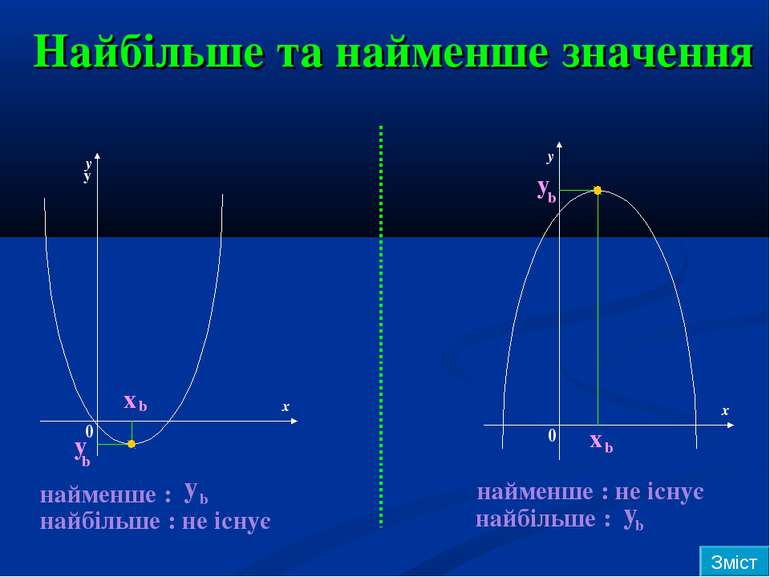
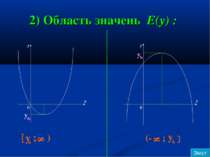
Найбільше та найменше значення y y y x x 0 0 y b x b y b x b найменше : найбільше : не існує y b найменше : не існує найбільше : y b Зміст

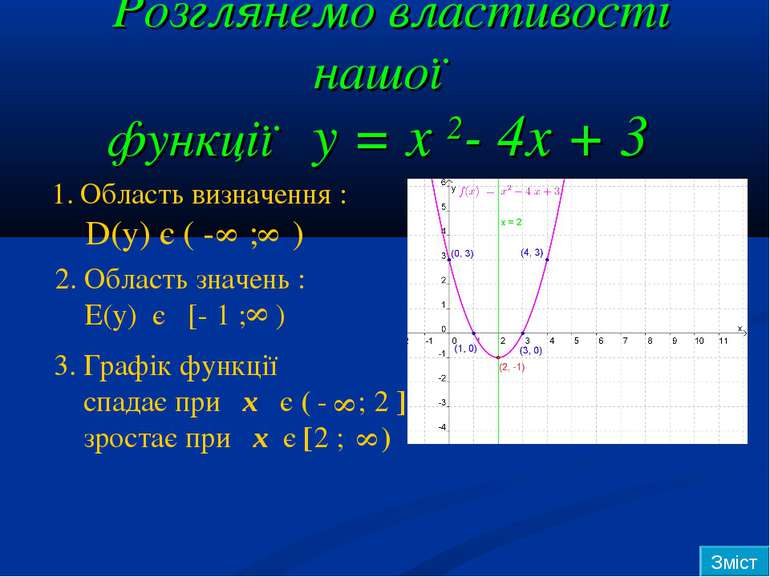
Розглянемо властивості нашої функції y = x 2- 4x + 3 Область визначення : D(у) є ( - ; ) 8 8 2. Область значень : Е(у) є [- 1 ; ) 8 3. Графік функції спадає при x є ( - ; 2 ] зростає при x є [2 ; ) 8 8 Зміст

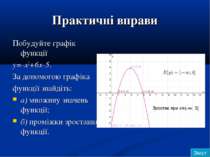
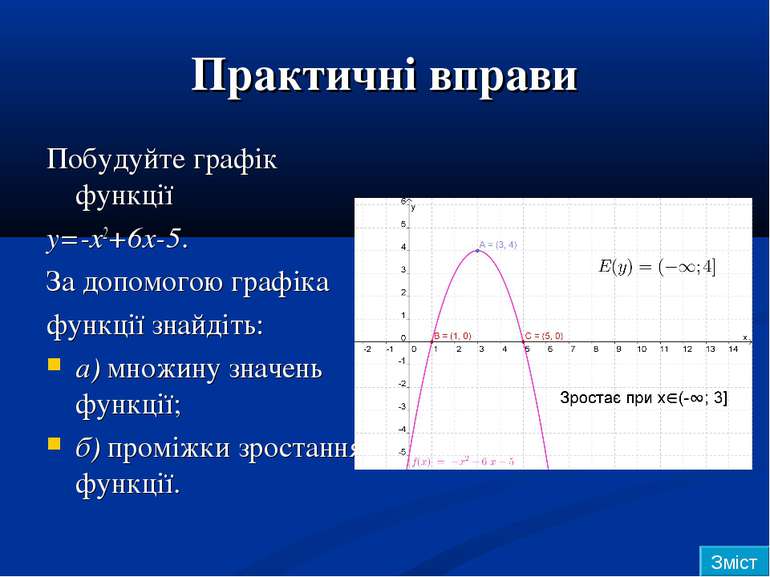
Практичні вправи Побудуйте графік функції y=-x2+6x-5. За допомогою графіка функції знайдіть: а) множину значень функції; б) проміжки зростання функції. Зміст

Підіб’ємо підсумки! 1) Квадратичною функцією називається функція , яку можна задати формулою ... Зміст

2) Графіком квадратичної функції є... 3) Графік квадратичної функції у = ах2+ bx + c симетричний відносно прямої... Зміст

4) Вітки параболи напрямленні вгору , якщо ... 5) Абсцису вершини параболи можна знайти за формулою ... Зміст

6) Значення х , при яких значення функції дорівнює нулю , називаються ... Зміст

Молодці всі ті , хто добре справився із даним завданням . Зміст

Отже , вивчиши даний матеріал , ви вмієте : * розпізнавати квадратичну функцію ; * знаходити координати вершини параболи та нулі функції ; * визначати напрямок віток графіка функції ; * будувати графік квадратичної функції ; * досліджувати властивості квадратичної функції .

Дякую за співпрацю і до зустрічі