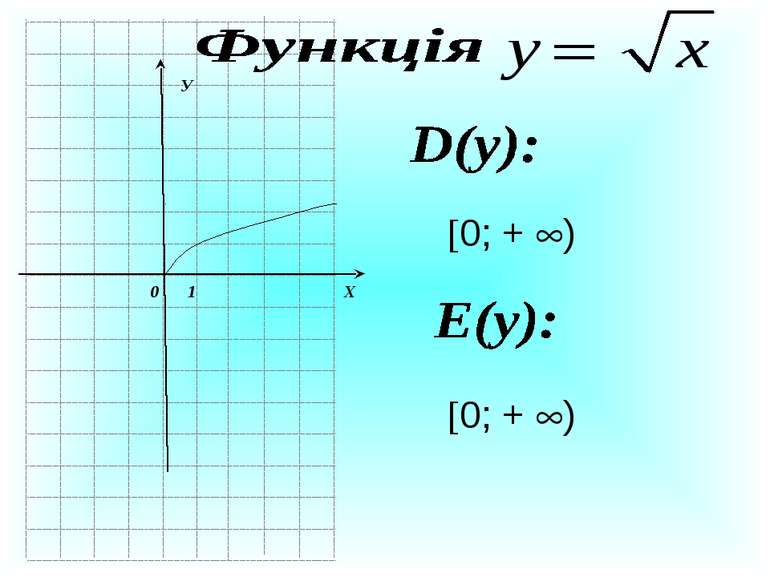
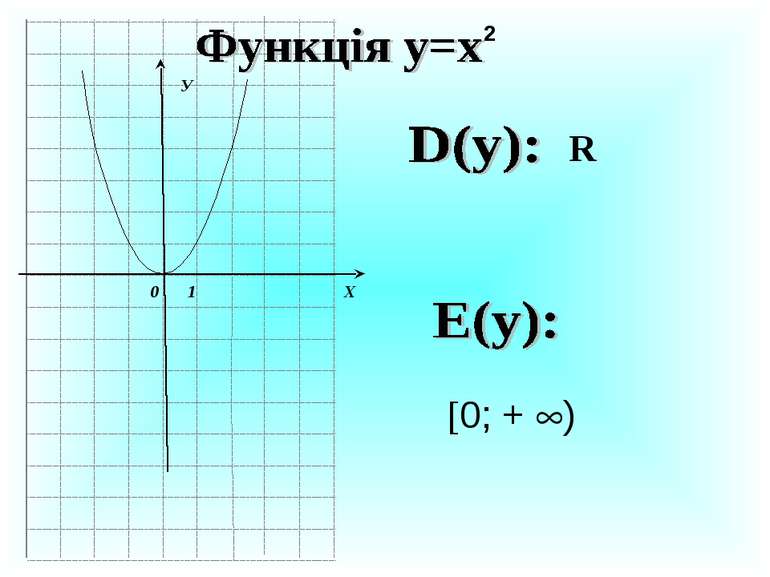
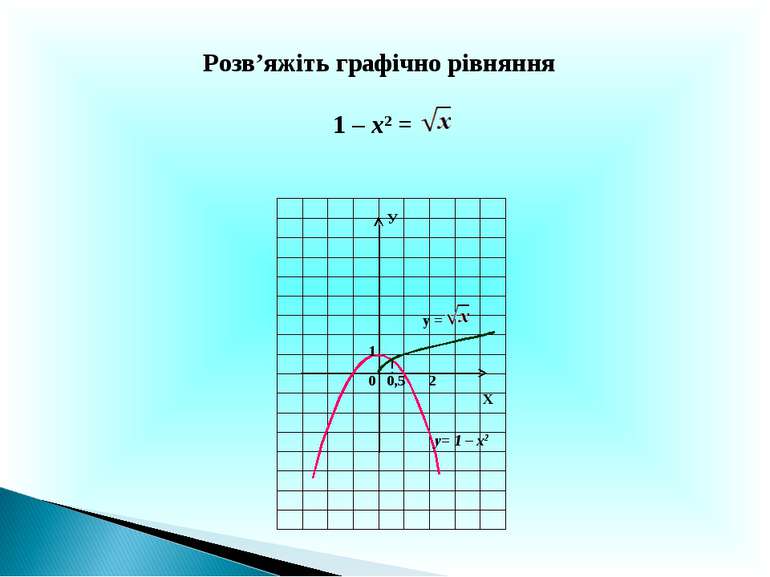
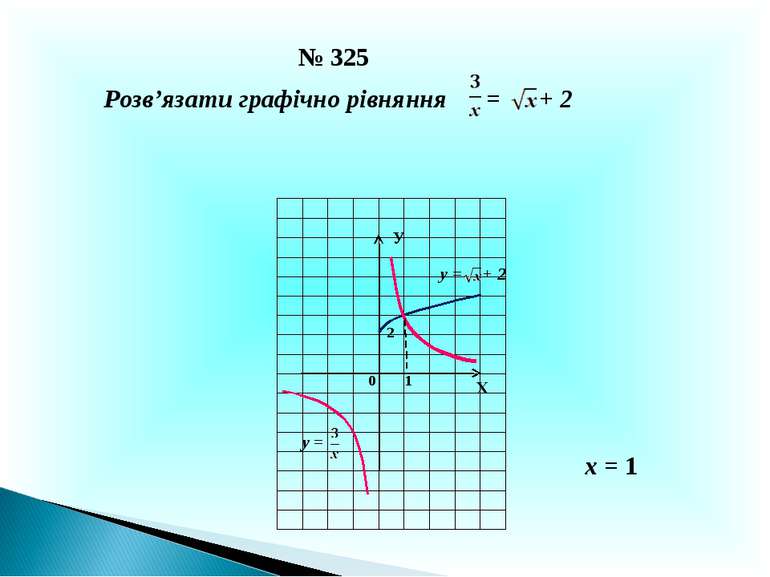
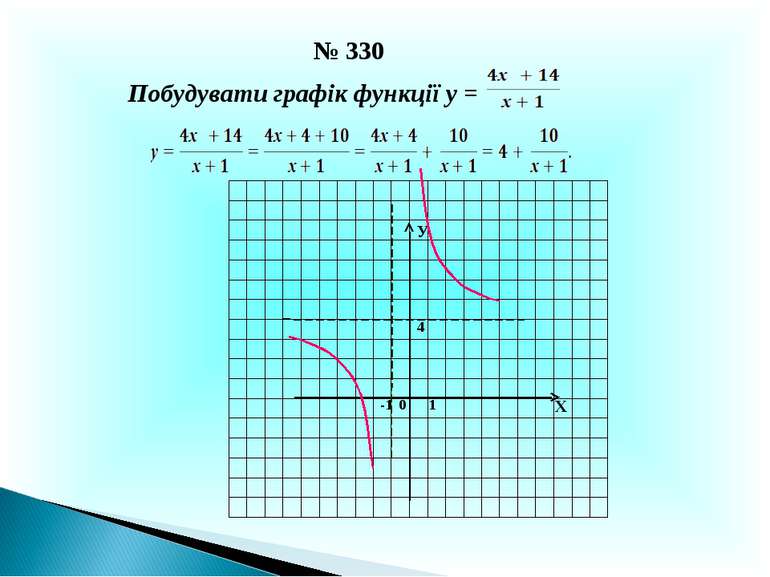
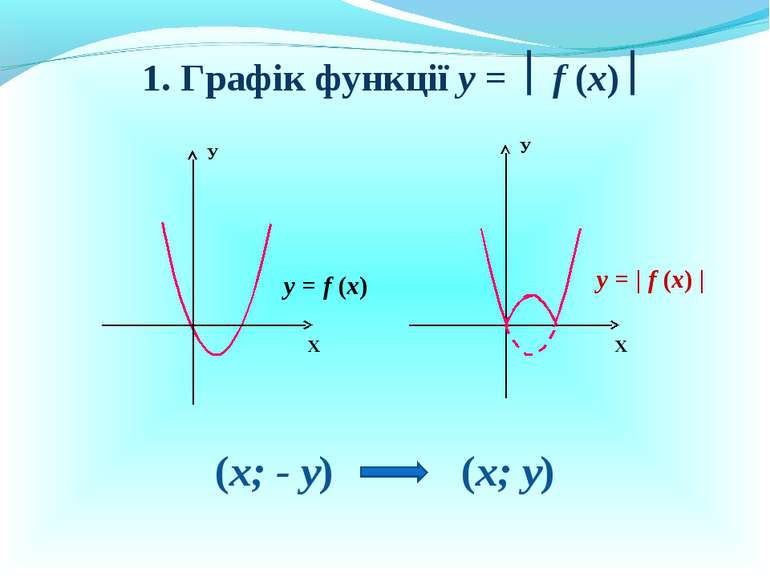
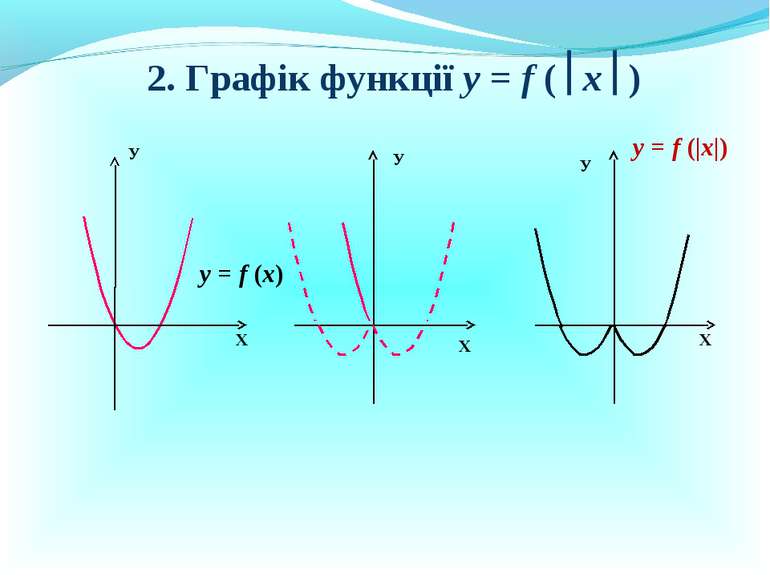
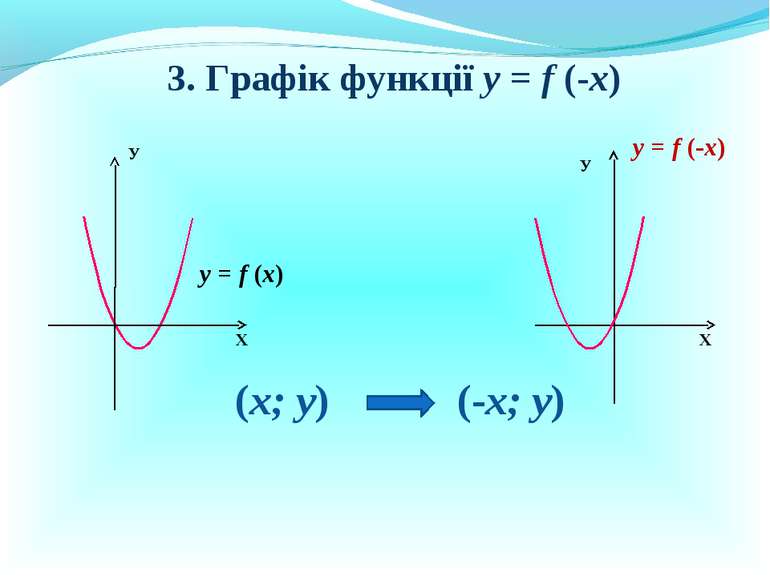
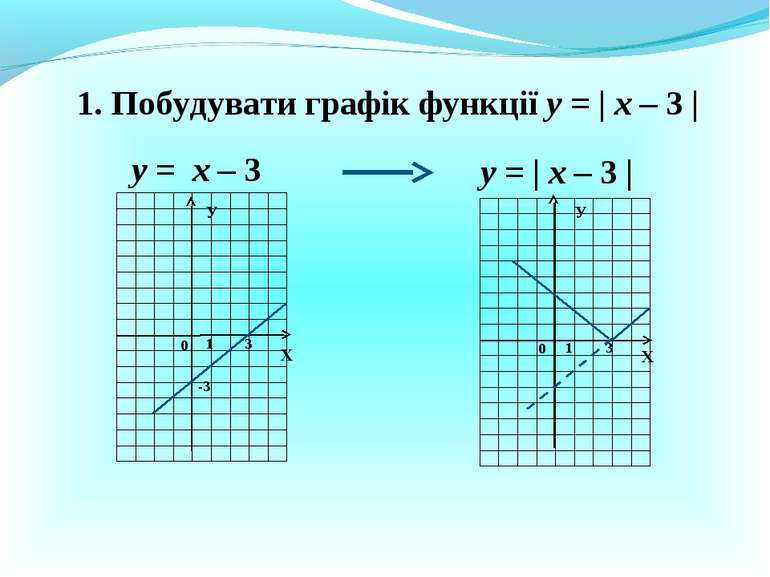
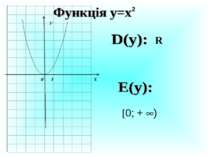
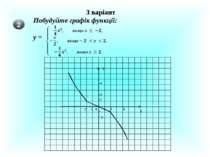
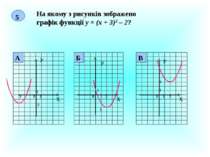
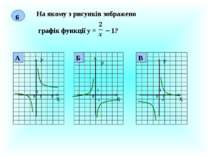
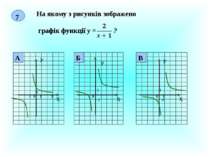
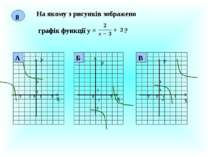
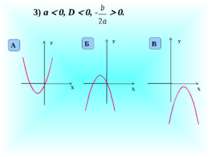
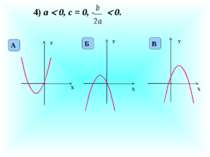
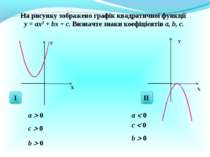
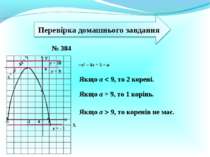
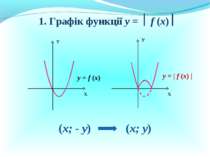
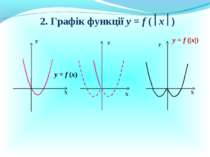
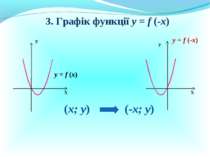
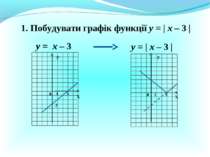
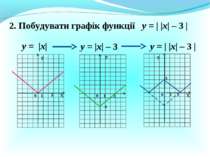
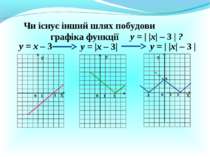
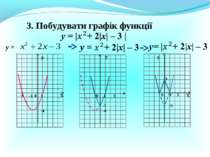
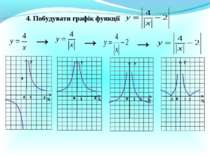
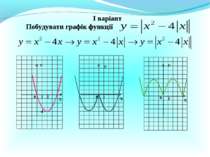
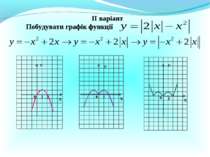
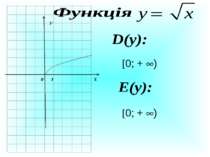Презентація на тему:
Квадратична функція 9 клас

Лисенко О. Є. м. Яготин Київської області

Уроки 1 2 3 4 5 6 7 8 9 10 11

Урок № 1 Х У

Якщо ви не сподіваєтеся знайти нічого несподіваного, то ви його не знайдете, оскільки це буде для вас непосильним. Геракліт

Тема уроку: Функція y = f (x) y = g (x)

Мета уроку: – систематизувати знання про функцію за 7-8 класи; – формувати навики знаходження значень функції при заданому значенні аргументу; області визначення функцій; – розвивати вміння читати графік функції.

Функція – це правило, за допомогою якого за кожним значенням незалежної змінної з множини Х можна знайти єдине значення залежної змінної. Область визначення функції – множина всіх значень, яких набуває аргумент. Область значень функції – множина всіх значень, яких набуває залежна змінна.

Способи задання функції: • аналітичний; • описовий; • за допомогою таблиці; • графічний.

Х У 0 1 k >0 Х Х У 0 1 k< 0

Х У 0 1 k >0 Х Х У 0 1 k< 0

Х У 0 1 k > 0 Х Х У 0 1 k< 0

X У 0 1 0; + ) 0; + )

X У 0 1 R 0; + ) 2

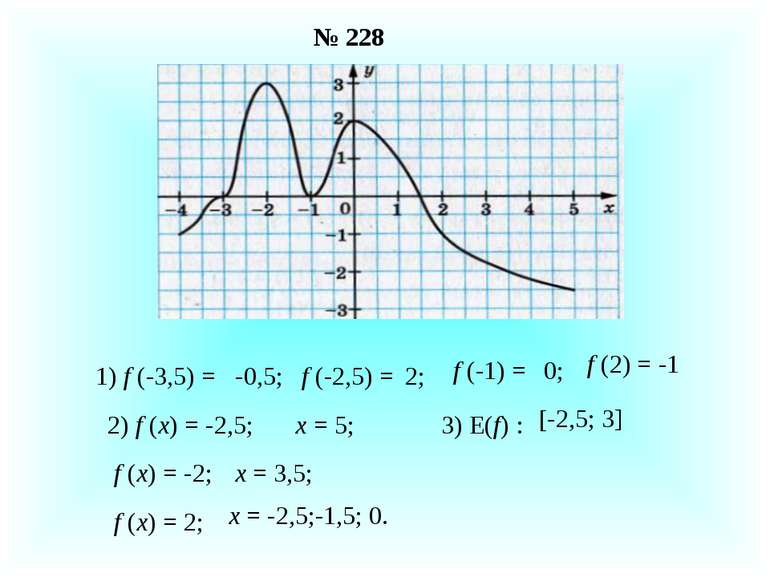
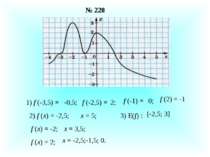
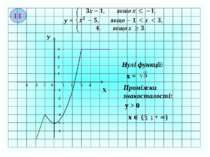
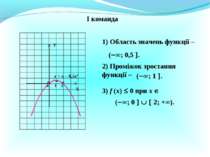
№ 228 1) f (-3,5) = -0,5; f (-2,5) = 2; f (-1) = 0; f (2) = -1 2) f (x) = -2,5; x = 5; f (x) = -2; x = 3,5; f (x) = 2; x = -2,5;-1,5; 0. 3) E(f) : -2,5; 3]

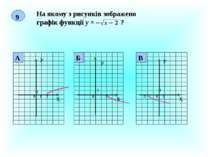
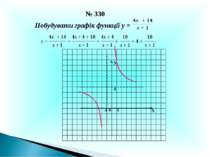
№ 230 Знайдіть область визначення функцій: R (- ; -5),(-5; + ) R [9; + ) (- ; -2), (-2; 2), (2; + ) [-6; 4] Функція Область визначення f (x) = 7x – 15 f (x) = f (x) = f (x) = f (x) = f (x) =

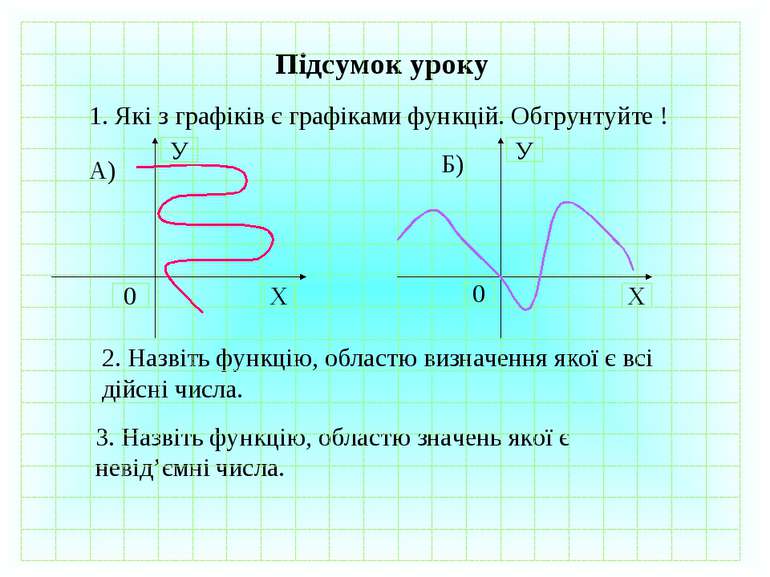
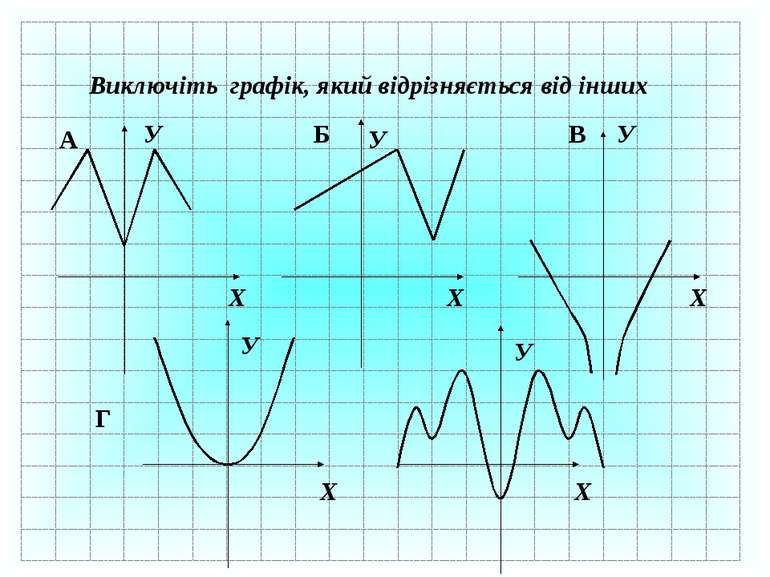
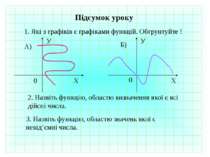
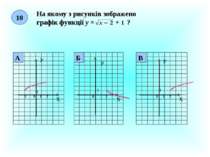
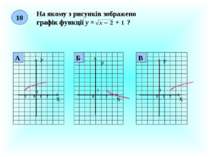
Підсумок уроку 2. Назвіть функцію, областю визначення якої є всі дійсні числа. 3. Назвіть функцію, областю значень якої є невід’ємні числа. 1. Які з графіків є графіками функцій. Обгрунтуйте ! Х У 0 Х У 0 А) Б)

Домашнє завдання: § 7, № 224, 229, 231(3-6)

Урок № 2 Х У

Математику не можна вивчати спостерігаючи, як це робить сусід. А. Нівен

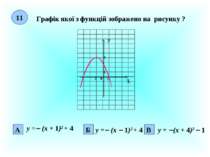
Тема уроку: Функція Мета уроку: – формувати навики знаходження області визначення, області значень функцій; – розвивати графічну культуру; – формувати вміння аналізувати, співставляти, обгрунтовувати свою думку.

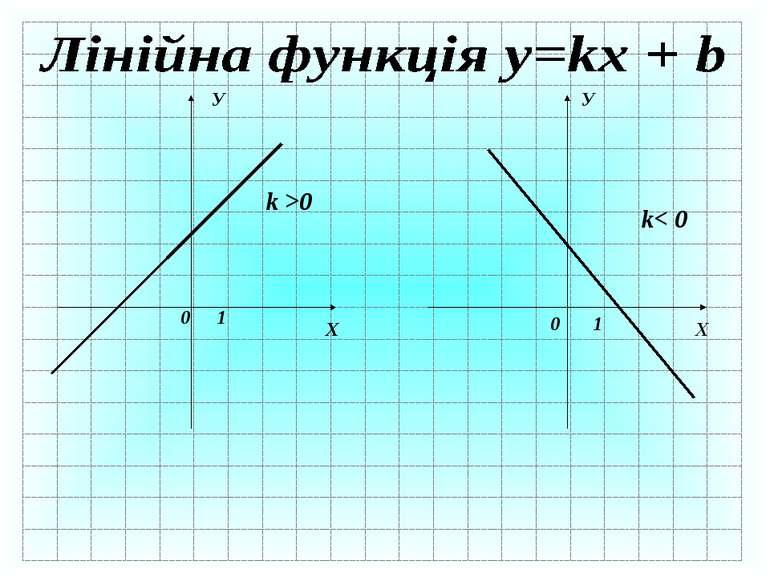
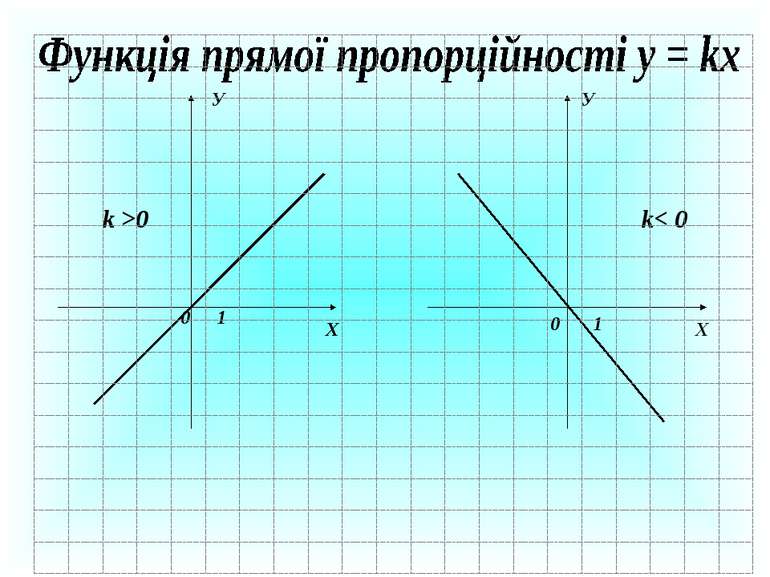
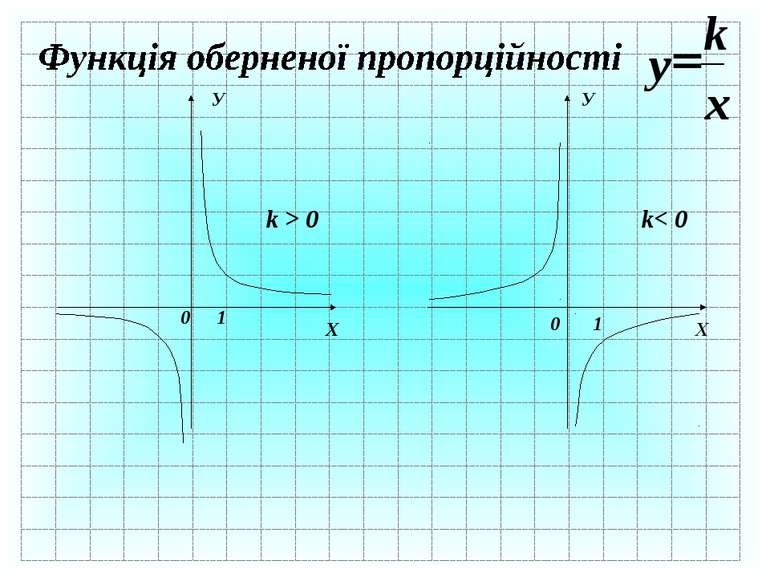
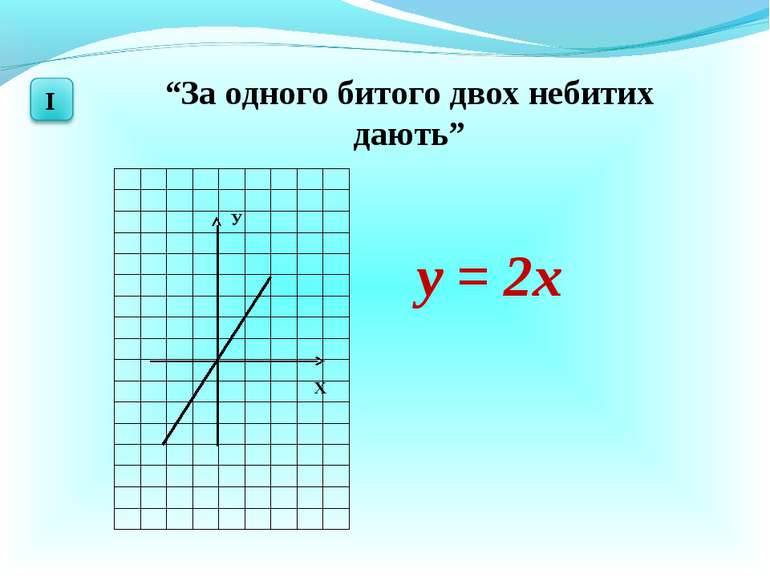
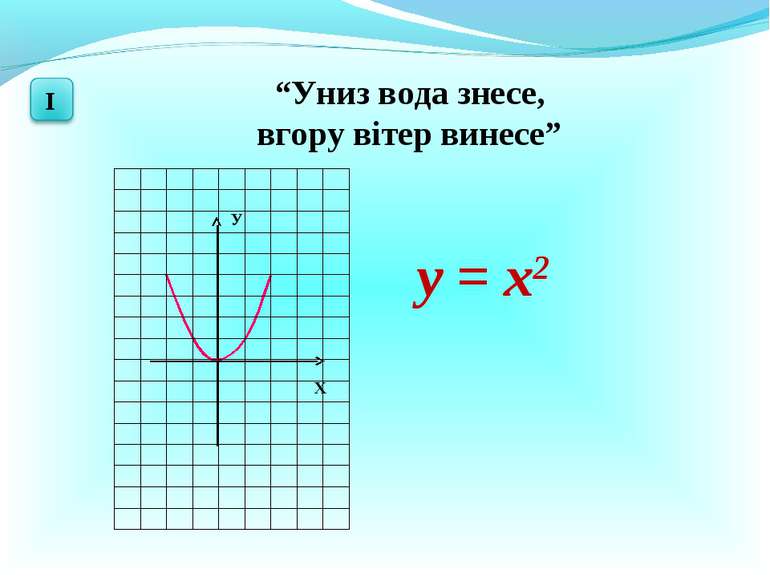
Які з даних функцій є : а) лінійними; б) функцією оберненої пропорційності ? у =2х – 3 у = х2 – 4 у = – 5х у = 8х-1 а) б) у = – 5х у =2х – 3 у = 8х-1

Серед даних функцій вибрати функції: а) областю визначення яких є всі дійсні числа; б) областю значень яких є множина додатних чисел. а) б)

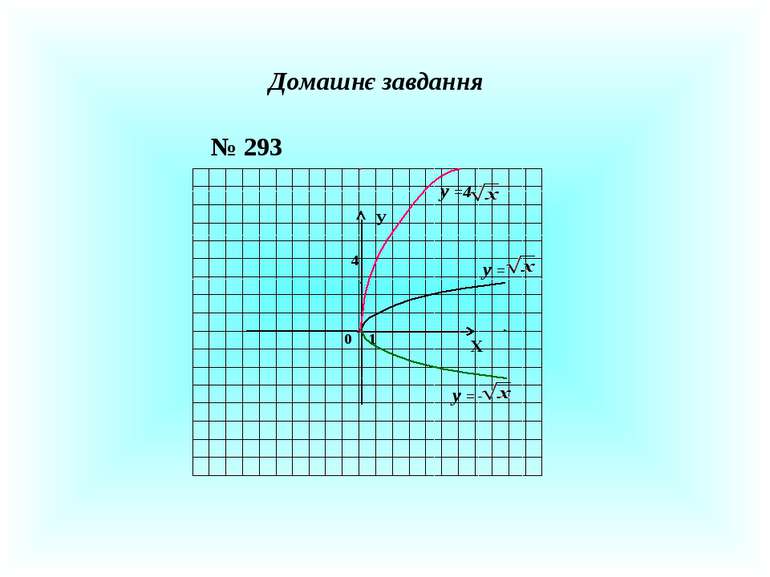
Домашнє завдання № 228 Встановіть відповідність між аргументом і значенням функції . f (3) f (0) f (-0,2) f (1,6) -2,6 2,8 7 -2

№ 237 Побудувати графік функції Х 0 У 1 -3

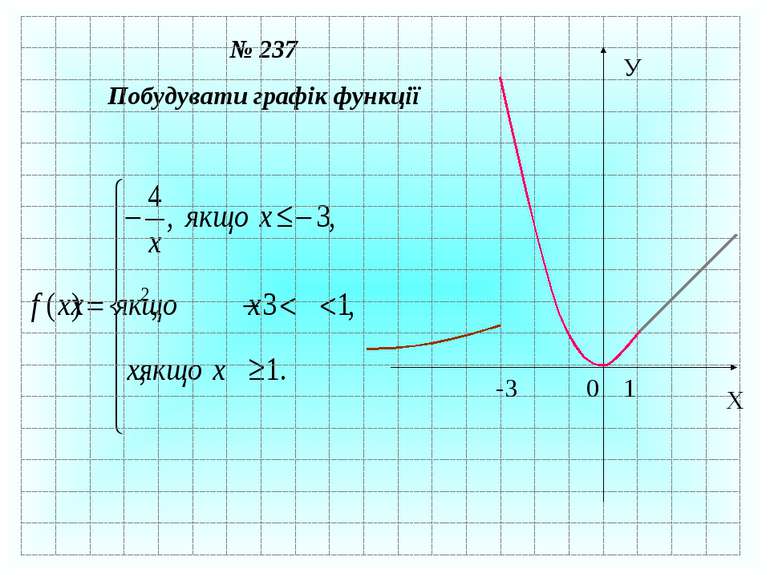
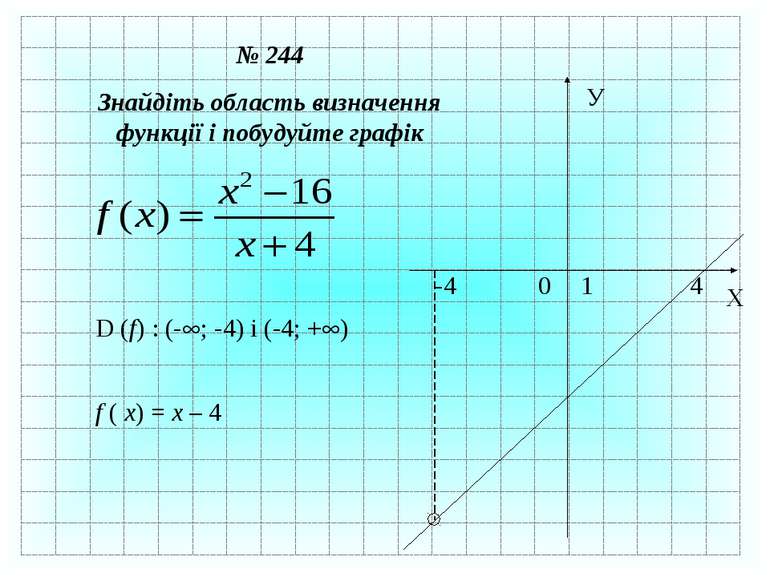
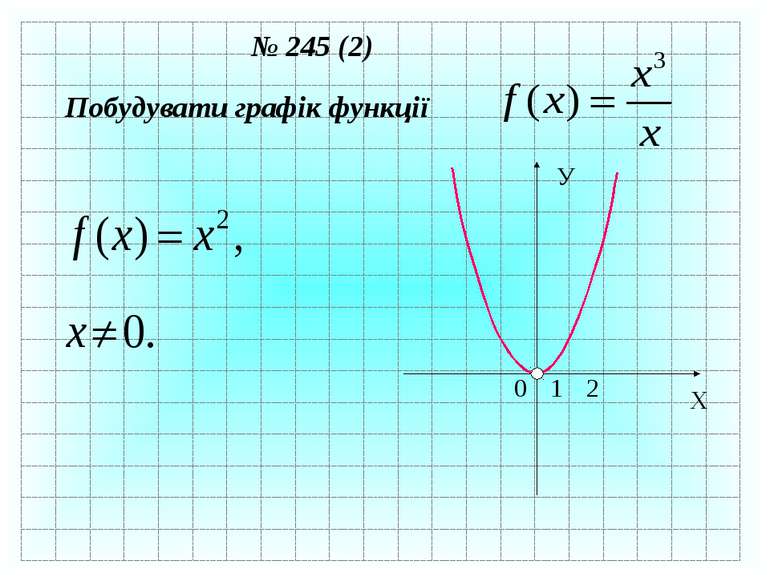
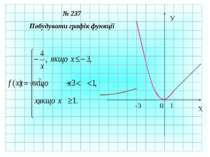
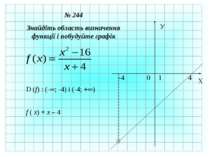
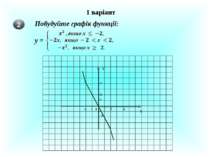
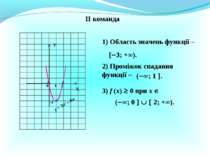
№ 244 Знайдіть область визначення функції і побудуйте графік D (f) : (- ; -4) і (-4; + ) f ( x) = x – 4 X У 0 1 4 -4

Підсумок уроку 1. Задайте формулою функцію, областю визначення якої є множина всіх чисел, більших 5. 2. Задайте формулою функцію, областю значень якої є множина від’ємних чисел. 3. Що буде графіком функції

f ( x ) = 1, x 3. X 0 У 1 1 3 -3

Домашнє завдання: § 7, № 224, 229, 231(3-6)

Урок № 3 Х У

Не все на світі просто є, Але якась закономірність саме в тому, Що істина раптово постає Крізь ліс ускладнень в самому простому! В. Коротич

Тема уроку: Мета уроку: Властивості функції дізнатися про нові властивості функції; працювати над вмінням знаходити нулі функції; вчитися бути уважним, відповідальним.

Перевірка домашнього завдання

№ 242 Встановіть відповідність між функціями і їх областями значень 1) f (x) = x2 + 3 2) f (x) = 6 – 3) f (x) = A. [ 0; + ) Б. [ 0; 3 ] В. ( – ; 6 ] Г. [ 3; + ) 1 – 2 – 3 – Г В А

Встановіть відповідність між функціями і їх областями визначеннями 1) f (x) = 2) f (x) = 3) f (x) = 4) f (x) = A. [ 0; + ) Б. ( – ; 0 ] В. (– ; 1) і (1; + ) Г. [ 1; + ) Д. ( – ; 1] 1 – 2 – 3 – 4 – Д Б В Г

№ 245 (2) Побудувати графік функції Х У 0 1 2

Х 0 У 1 2 6 1 3 8 4 –2 –7 –4 –8 –6 5 –2 –3 Читаємо графік !

Виключіть графік, який відрізняється від інших Х У Х У Х У Х У Х У А Б В Г

Знайдіть графіки, які мають однакову властивість Х У Х У Х У Х У Х У А Б В Г Д

Добудувати графік функції А) парна А) непарна Х У Х У

Домашнє завдання: § 2, п. 8, № 254, 257

Урок № 4 Х У

Зібратися разом – це початок, триматися разом – це прогрес, працювати разом – це успіх. Г. Форд

Тема уроку: Функції і їх властивості Мета уроку: Закріпити здобуті знання, показати вміння використовувати їх для розв’язання завдань

Перевірка домашнього завдання Знайдіть помилки № 254 – 1; 3; ( - 1; 3); ( 1; + ∞ ); ( - ∞; 3 .

№ 257 1. Назвіть функцію, яка має один нуль. 2. Яка з функції не має нулів? f(x) = - 5 3. Нулями якої з функцій є числа 0 і 1? f(x) = х2 - х

Практичне заняття ІІ ІІІ

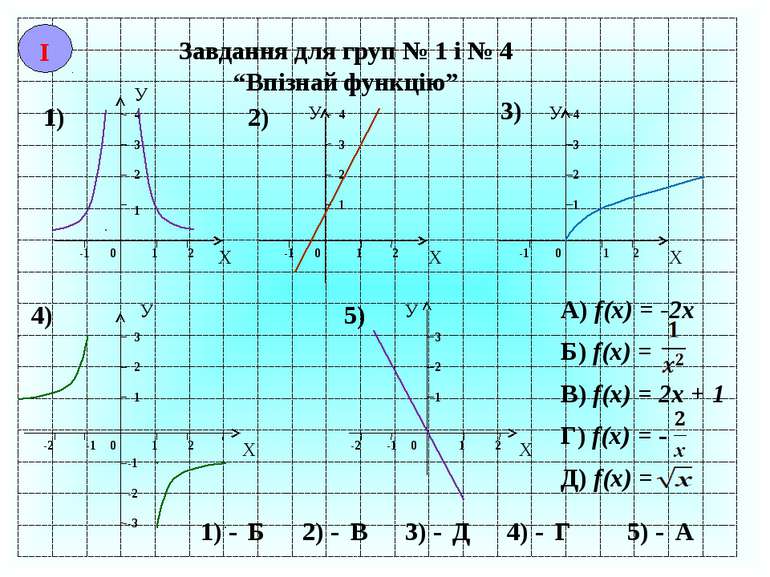
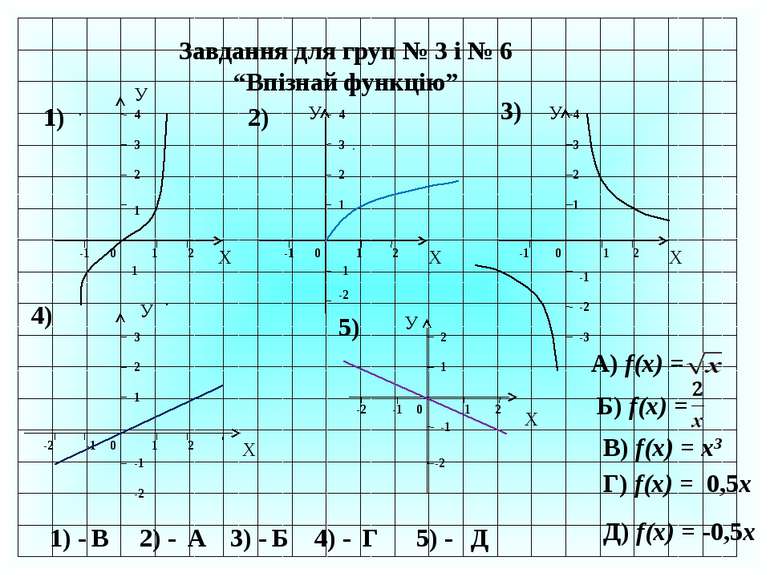
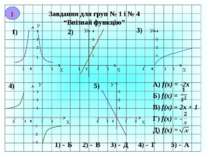
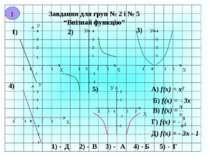
Завдання для груп № 1 і № 4 “Впізнай функцію” Х У -1 0 1 2 1 2 3 4 1) У Х -1 0 1 2 1 2 3 4 2) У Х -1 0 1 2 1 2 3 4 3) 4) 5) У Х 1 0 -1 -2 2 1 2 3 -1 -2 -3 У Х 1 2 -1 0 -2 1 2 3 A) f(x) = -2x Б) f(x) = В) f(x) = 2x + 1 Г) f(x) = - Д) f(x) = 1) - 2) - 3) - 4) - 5) - Б В Д Г А І

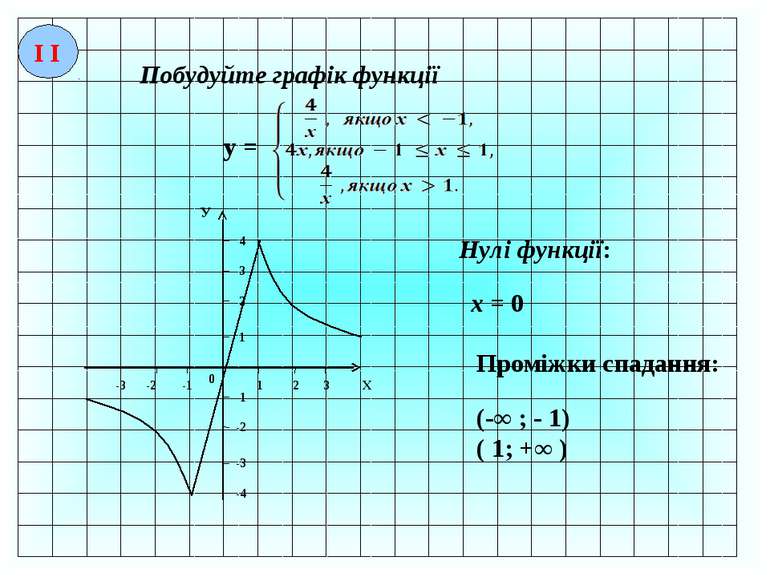
І І Побудуйте графік функції у = Укажіть нулі функції, проміжки знакосталості. ІІІ Знайдіть при якому найменшому цілому значенню а функція у = х2 + 6х + а не має нулів.

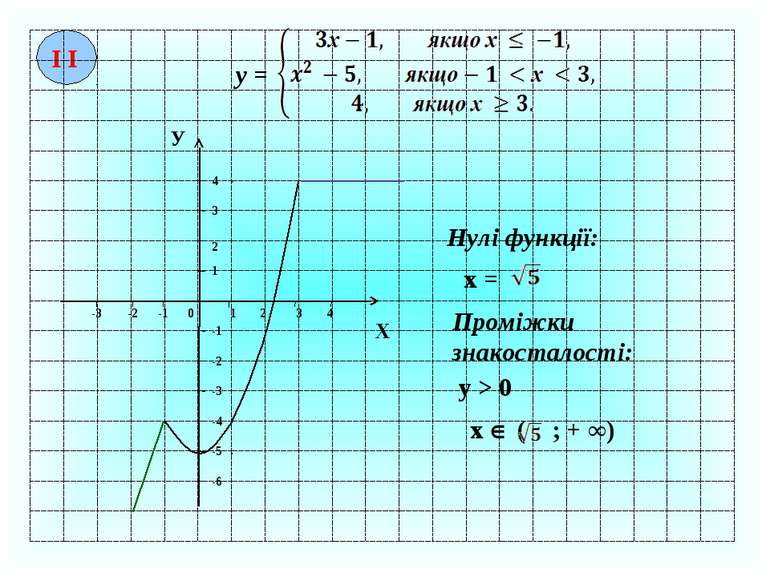
І І у = -1 2 3 4 1 2 3 4 0 -2 -3 -1 -2 -3 -4 -5 -6 Х У 1 Нулі функції: х = Проміжки знакосталості: y > 0 x ( ; + ∞)

ІІІ Знайдіть при якому найменшому цілому значенню а функція у = х2 + 6х + а не має нулів. х2 + 6х + а ≠ 0, D = b2 – 4ac < 0, 36 – 4a < 0, 4a < - 36, a > 9. Відповідь: а = 10.

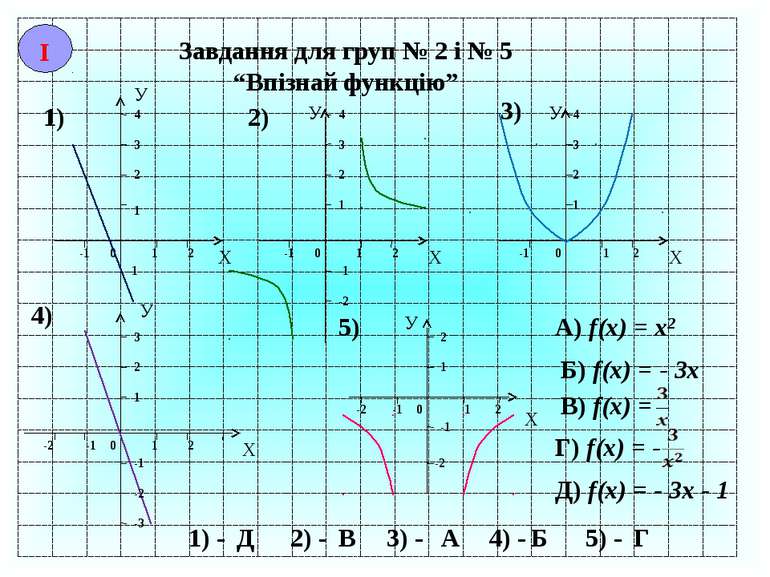
Завдання для груп № 2 і № 5 “Впізнай функцію” Х У -1 0 1 2 1 2 3 4 1) У Х -1 0 1 2 1 2 3 4 2) У Х -1 0 1 2 1 2 3 4 3) 4) 5) У Х 1 0 -1 -2 2 1 2 3 -1 -2 -3 У Х 1 2 -1 0 -2 -1 -2 1 2 -1 -2 -1 А) f(x) = x2 Б) f(x) = - 3x В) f(x) = Г) f(x) = -   Д) f(x) = - 3x - 1 1) - 2) - 3) - 4) - 5) - Д В А Б Г І

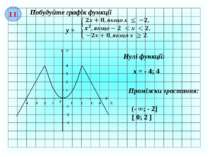
І І Побудуйте графік функції у = Укажіть нулі функції, проміжки зростання. ІІІ Знайдіть при якому найбільшому цілому значенню п функція у = (8 – 3п)х – 7 є зростаючою .

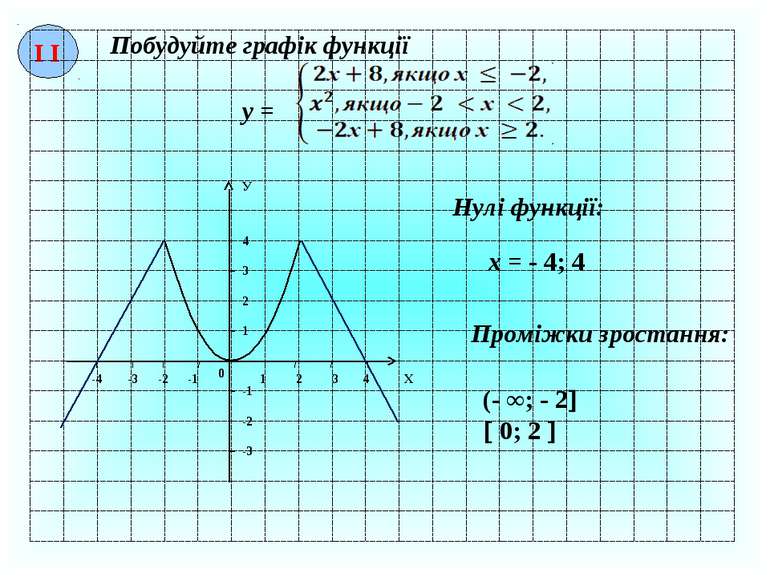
І І Побудуйте графік функції у = 1 2 3 4 1 2 3 4 0 -1 -2 -3 -4 -1 -2 -3 Х У Нулі функції: х = - 4; 4 Проміжки зростання: (- ∞; - 2 0; 2

Знайдіть при якому найбільшому цілому значенню п функція у = (8 – 3п)х – 7 є зростаючою . ІІІ 8 – 3п 0, 3п - 8, п . Відповідь: п = 2.

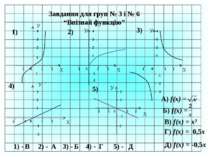
Завдання для груп № 3 і № 6 “Впізнай функцію” Х У -1 0 1 2 1 2 3 4 1) У Х -1 0 1 2 1 2 3 4 2) У Х -1 0 1 2 1 2 3 4 3) 4) 5) У Х 1 0 -1 -2 2 1 2 3 -1 -2 У Х 1 2 -1 0 -2 -1 -2 1 2 -1 -2 -1 -1 -2 -3 А) f(x) = Б) f(x) = В) f(x) = х3 Д) f(x) = -0,5х Г) f(x) = 0,5х 2) - 3) - 4) - 1) - 5) - А В Г Б Д

І І Побудуйте графік функції у = Укажіть нулі функції, проміжки спадання. ІІІ Знайдіть при якому найбільшому цілому значенню с функція у = сх – с – 3 + 2х буде спадною.

Побудуйте графік функції І І у = -1 2 3 1 3 2 4 0 -2 -3 -1 -2 -3 -4 Х У 1 Нулі функції: х = 0 Проміжки спадання: (-∞ ; - 1) ( 1; +∞ )

ІІІ Знайдіть при якому найбільшому цілому значенню с функція у = сх – с – 3 + 2х буде спадною. у= сх – с – 3 + 2х, у= х (с + 2) – с – 3, с + 2 0, с - 2 . Відповідь: с = - 3.

МОЛОДЦІ! Підсумок уроку:

Домашнє завдання

Урок № 5 y = f(x) y = -f(x) X У

Не достатньо знати, необхідно також застосувати. А. Франс

Тема уроку: Графік функції у = k f(x) Мета уроку: Перевірити вміння використовувати здобуті знання для розв’язання завдань, навчитися будувати графік функції у = k f(x) за відомим графіком у = f(x)

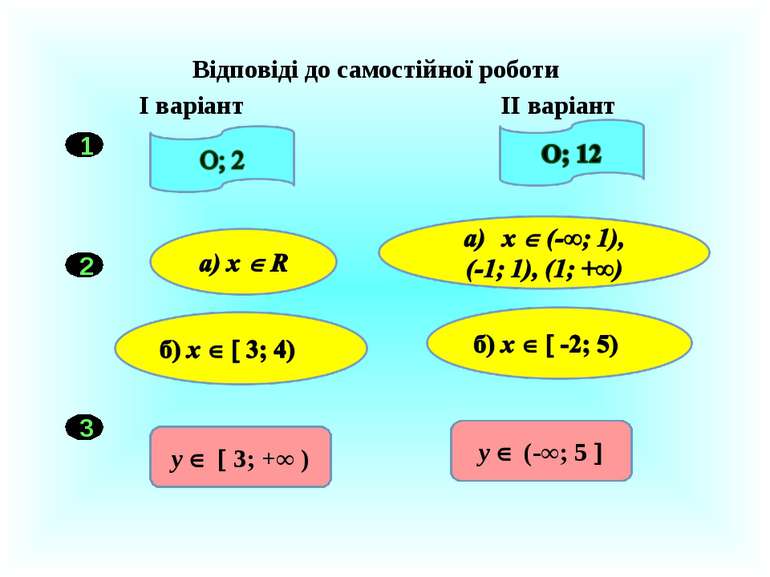
Самостійна робота з самоперевіркою І варіант ІІ варіант 1 Знайдіть нулі функції: f(x) = - 3x2 + 6x f(x) = 0,25x2 – 3x 2 Знайдіть область визначення функції: 3 Знайдіть область значень функції: f(x) = 2 f(x) = - x2 + 5

Відповіді до самостійної роботи І варіант ІІ варіант 1 2 3 у 3; +∞ ) у (-∞; 5

X 2 1 2 3 0 1 2 3 4 5 У -1 -2 -3 -1 х у - 2 4 - 1 1 0 0 1 1 2 4

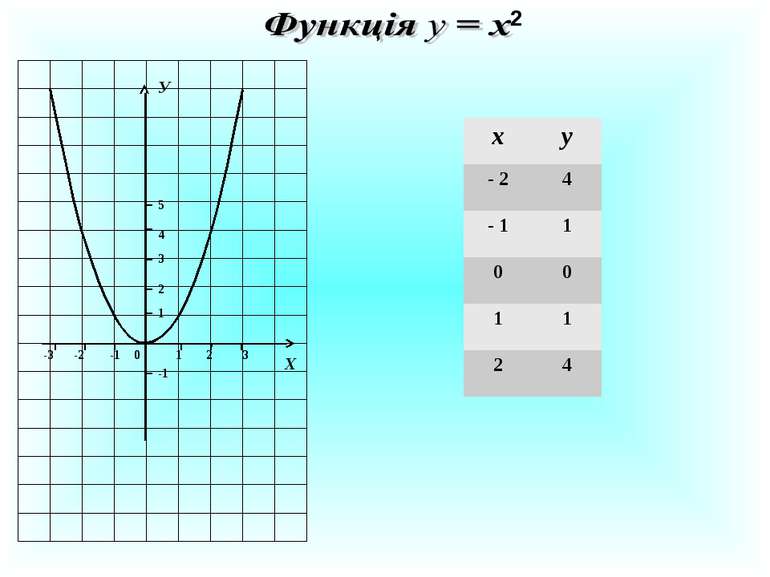
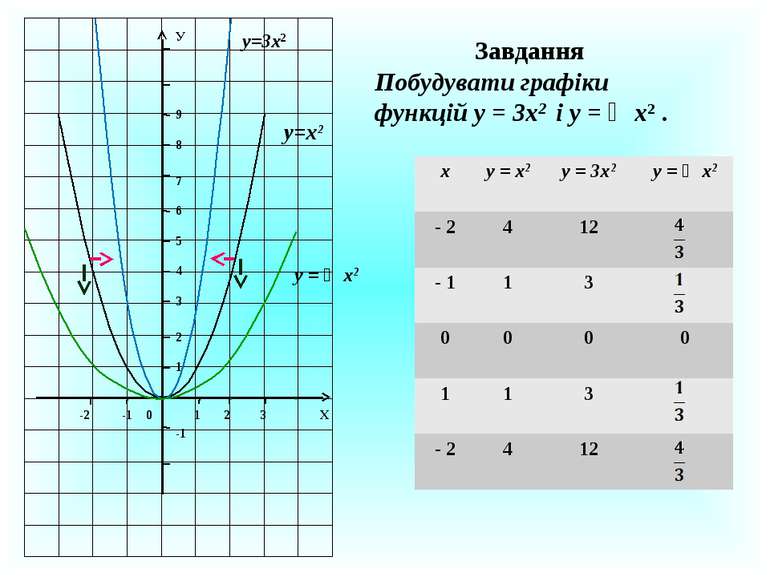
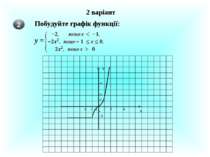
Завдання Побудувати графіки функцій у = 3х2 і у = ⅓х2 . 1 2 3 Х 1 2 3 4 5 6 7 8 9 0 -1 -2 -1 У у=х2 у=3х2 у = ⅓х2 х у = х2 у = 3х2 у = ⅓х2 - 2 4 12 - 1 1 3 0 0 0 0 1 1 3 - 2 4 12

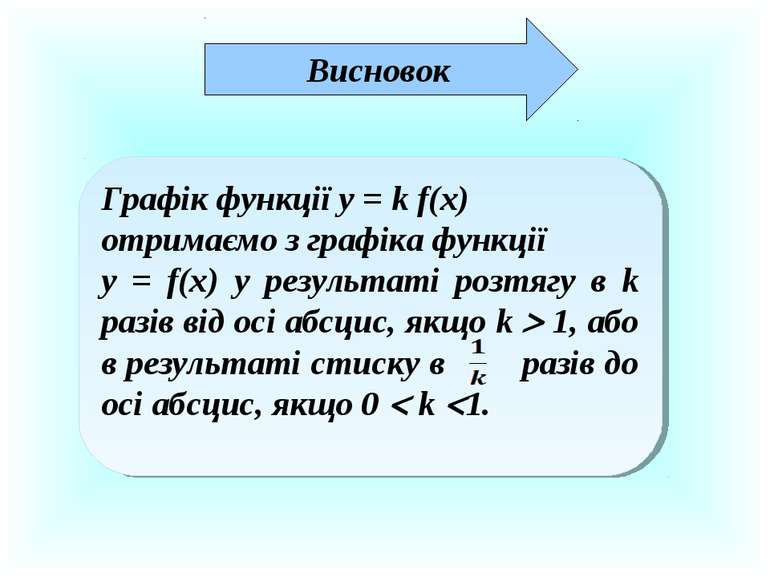
Висновок Графік функції у = k f(x) отримаємо з графіка функції у = f(x) у результаті розтягу в k разів від осі абсцис, якщо k 1, або в результаті стиску в разів до осі абсцис, якщо 0 k 1.

1 0 1 Х У 1 У Х 1 0 у = х2 у = -х2 у = 3 х2 у = -3 х2

1 0 1 Х У 1 У Х 1 0 у = ⅓х2 у = -⅓х2 y = f(x) y = -f(x) y = 0,5f(x)

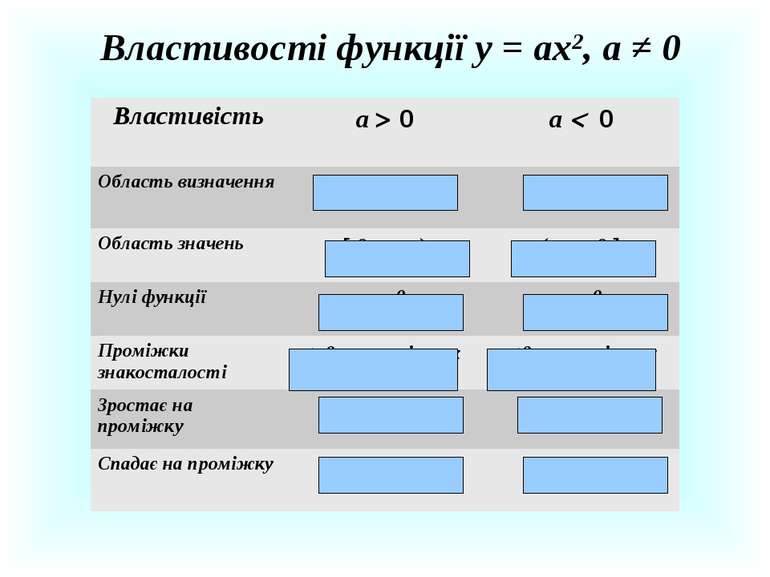
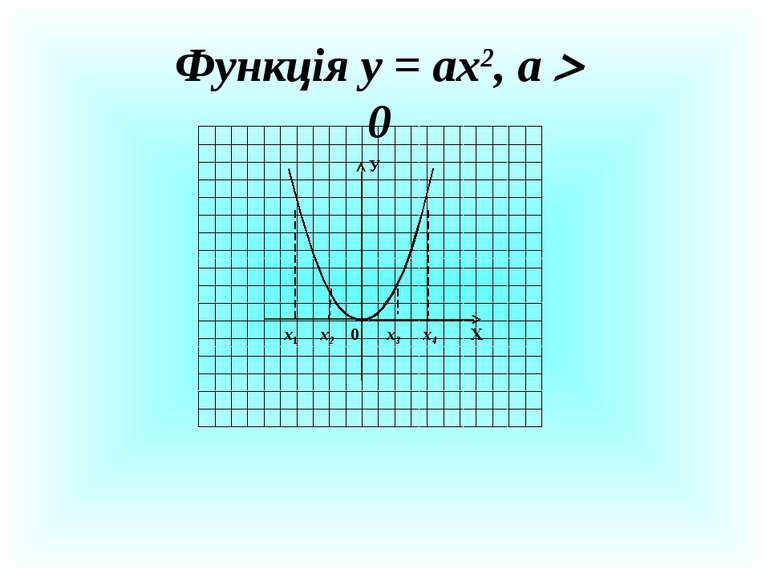
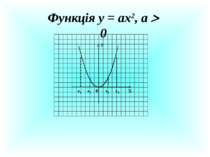
Властивості функції у = ах2, а ≠ 0 Властивість а 0 а 0 Область визначення (- ; + ) (- ; + ) Область значень 0; + ) ( - ; 0 Нулі функції х = 0 х = 0 Проміжки знакосталості у 0 на проміжках (- ; 0) і (0; + ) у 0 на проміжках (- ; 0) і (0; + ) Зростає на проміжку 0; + ) ( - ; 0 Спадає на проміжку ( - ; 0 0; + )

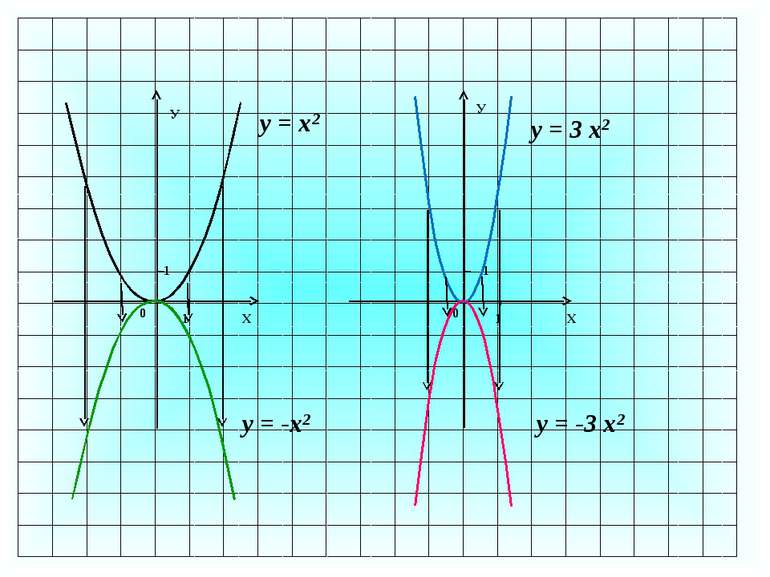
Підсумок уроку Як побудувати графік функції у = 6х2 , використовуючи при цьому графік функції у = х2? Що відбувається з графіком у = 6х2 при побудові графіка у = -6х2 ? Яка точка є вершиною параболи у = ах2 ? Де знаходиться графік функції у = ах2 при а 0? Що ви нового відкрили на уроці для себе? Які труднощі були при вивченні нового матеріалу? МОЛОДЦІ!

Домашнє завдання Вивчити п. 9 № 282, 287

Урок № 6

Як приємно дізнатися, що ти чогось дізнався. Ж. Мольєр

Тема уроку: Графік функції у = k f(x) Мета уроку: Формувати практичні навики по побудові графіків функцій; розвивати логічне мислення; почуття відповідальності

Вправа “Незакінчені речення”

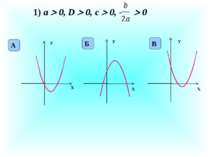
Графіком функції у = ах2, де а ≠ 0 є … парабола Якщо а 0, то графік функції у = ах2 розміщений … в І і ІІ координатних чвертях Область визначення функції у = 4х2 … ( - ∞; + ∞ ) Область значень функції у = -10х2 … ( - ∞; 0 Проміжок зростання функції у = 5х2 … 0; + ∞ ) Функція у = ах2, де а ≠ 0 має нуль … х = 0 Найбільше значення функції у = ах2 при а 0 … не існує

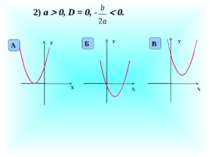
8. Проміжок, де у 0, для функції у = ах2, а 0, … ( - ∞; 0 ) і ( 0; + ∞ ) 9. Найбільше значення функції у = -3х2 … 0 10. Графік функції у = 4х2 отримаємо з графіка функції у = х2 в результаті …розтягу його в 4 рази від осі абсцис 11. Графік у = отримаємо з графіка у = х2 в результаті…стиску його в рази до осі абсцис 12. При побудові графіка функції у = - враховуємо, що всі значення функції у = , крім 0, міняються на … протилежні Молодці!

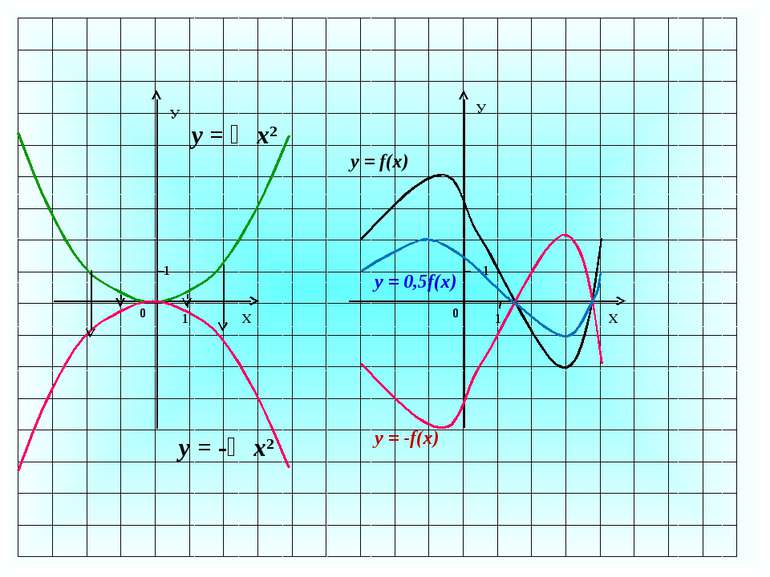
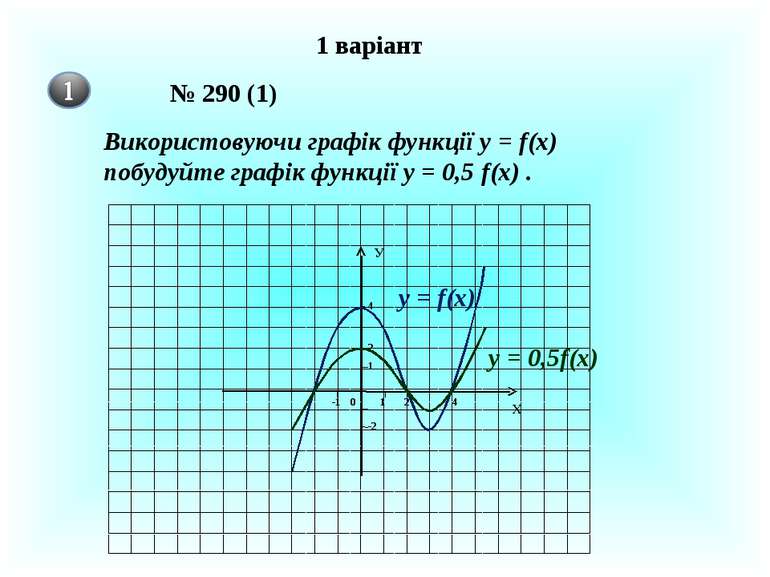
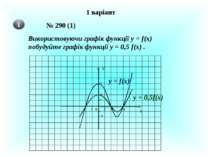
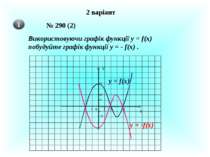
1 варіант № 290 (1) Використовуючи графік функції у = f(x) побудуйте графік функції у = 0,5 f(x) . 1 2 4 1 2 4 0 -1 -2 Х У y = f(x) y = 0,5f(x)

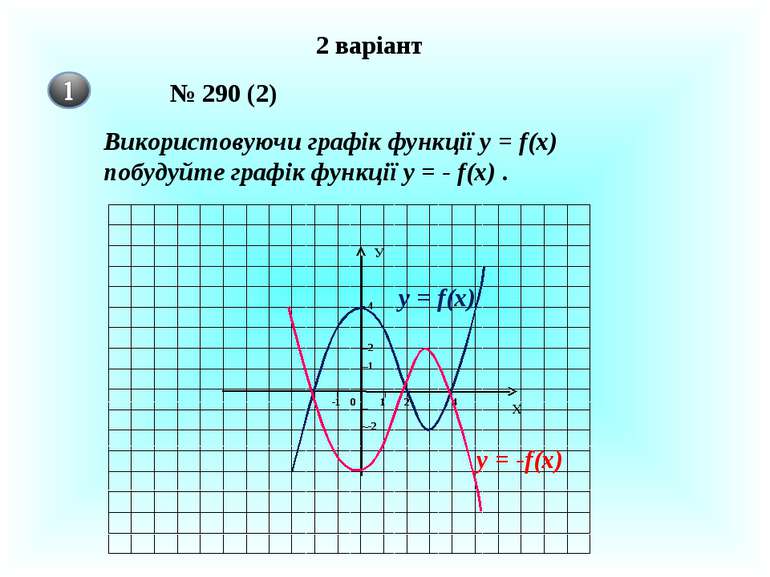
2 варіант № 290 (2) Використовуючи графік функції у = f(x) побудуйте графік функції у = - f(x) . 1 2 4 1 2 4 0 -1 -2 Х У y = f(x) y = -f(x)

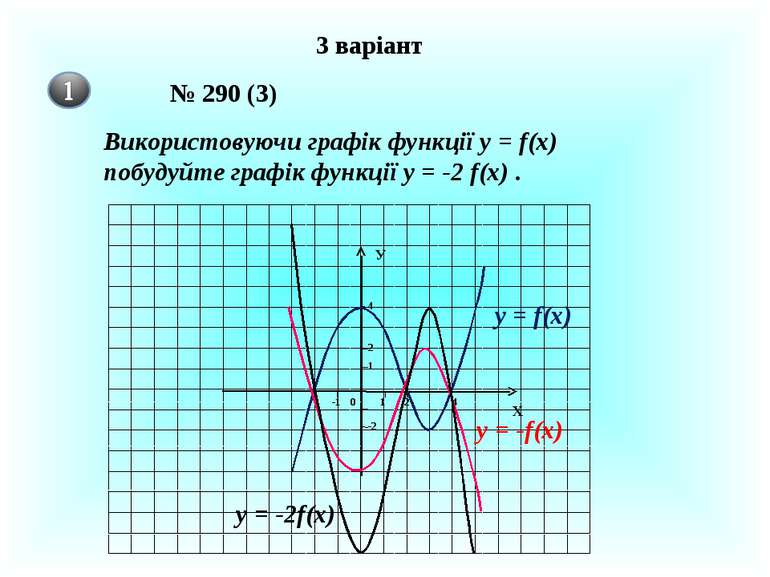
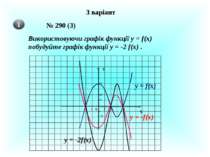
3 варіант № 290 (3) Використовуючи графік функції у = f(x) побудуйте графік функції у = -2 f(x) . 1 2 4 1 2 4 0 -1 -2 Х У y = f(x) y = -f(x) y = -2f(x)

1 варіант 1 2 4 1 2 4 0 -1 -2 Х У Побудуйте графік функції: у = -2

2 варіант 1 2 4 1 2 4 0 -1 -2 Х У Побудуйте графік функції: у = -2

3 варіант 1 2 4 1 2 4 0 -1 -2 Х У Побудуйте графік функції: у = -2

Задача на доведення

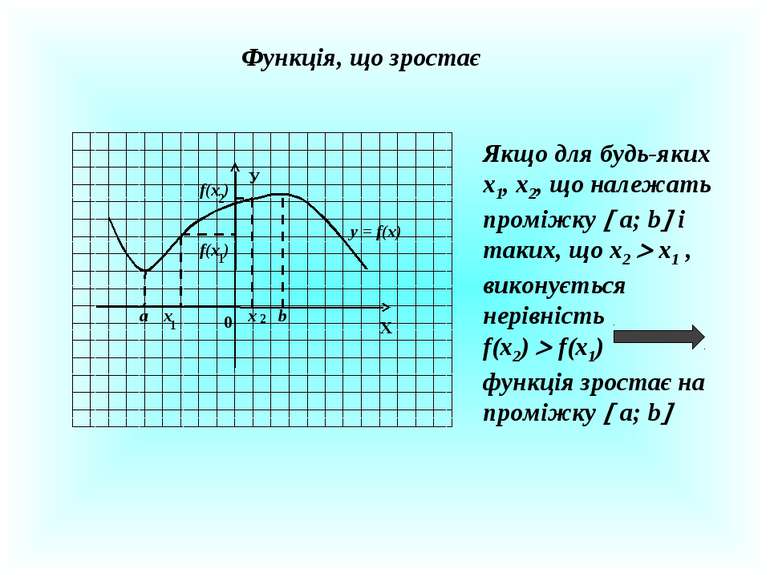
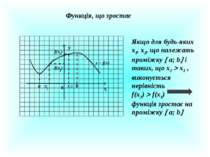
Функція, що зростає Х У 0 x x 1 2 f(x ) f(x ) 1 2 y = f(x) а b Якщо для будь-яких х1, х2, що належать проміжку а; b і таких, що х2 х1 , виконується нерівність f(x2) f(x1) функція зростає на проміжку а; b

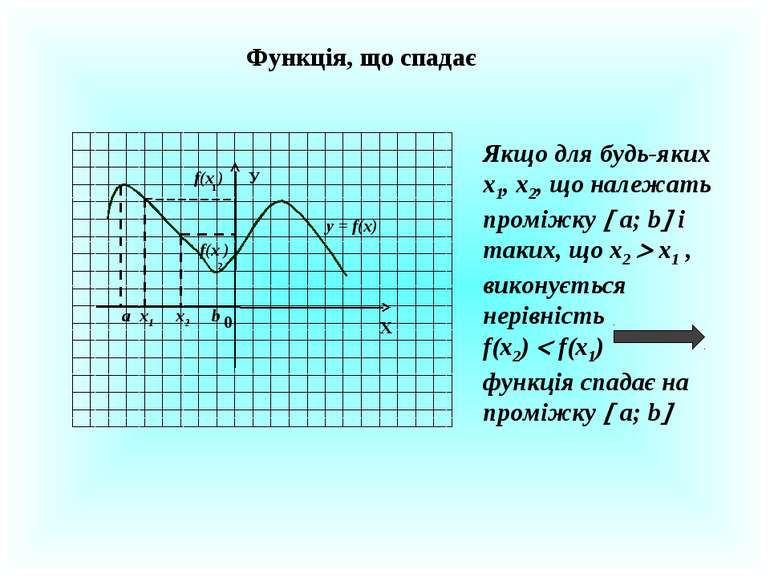
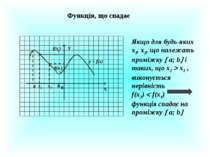
Функція, що спадає Х У 0 x2 х1 f(x ) f(x ) 2 1 y = f(x) а b Якщо для будь-яких х1, х2, що належать проміжку а; b і таких, що х2 х1 , виконується нерівність f(x2) f(x1) функція спадає на проміжку а; b

Функція у = ах2, а 0 Х У 0 х1 х2 х3 х4

Підсумок уроку

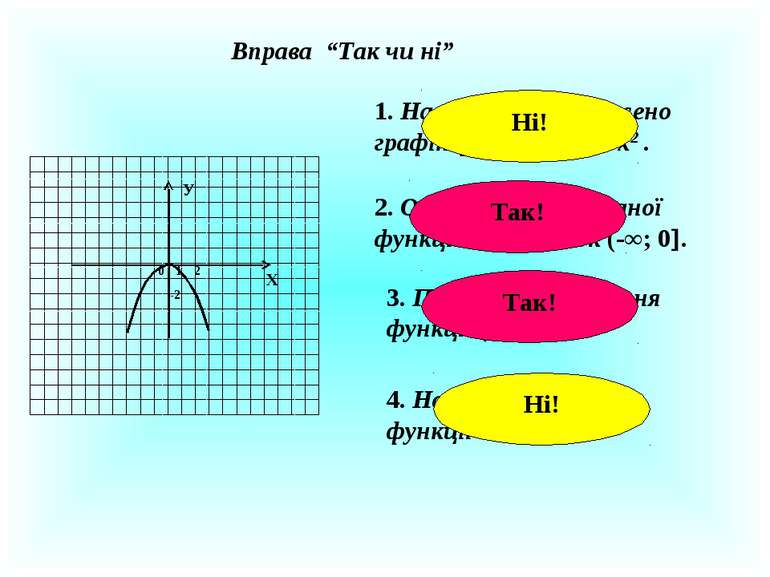
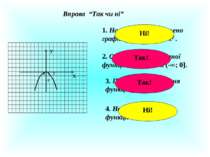
Вправа “Так чи ні” 1. На малюнку зображено графік функції у = 0,5х2 . 2. Область значень даної функції – проміжок (-∞; 0 . 3. Проміжок зростання функції (-∞; 0 . 4. Найменше значення функції 0. 0 У 1 2 Х -2 Ні! Так! Так! Ні!

Домашнє завдання Вивчити п. 9, № 293, 295 Підготуватися до роботи в групах

Урок № 7

Відкриття – це 10% натхнення і 90% праці. Т. Едісон

Тема уроку: Графіки функцій у = f(x) + а, у = f(x + а) Мета уроку: Навчитися як за допомогою графіка функції у = f(x) будувати графіки функцій у = f(x) + а, у = f(x + а); розвивати графічну культуру; вміння працювати в групах

Домашнє завдання № 293 Х У 1 0 у = у =4 у = - 4

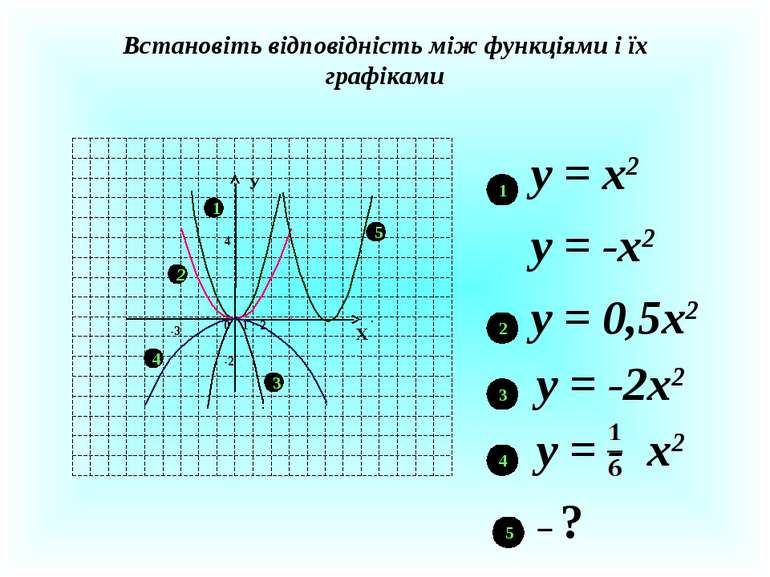
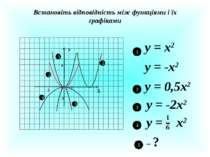
Встановіть відповідність між функціями і їх графіками Х У 1 0 2 4 -2 1 2 3 -3 4 5 у = х2 у = -х2 у = 0,5х2 у = -2х2 у = - х2 1 2 3 4 5 ?

Робота в групах

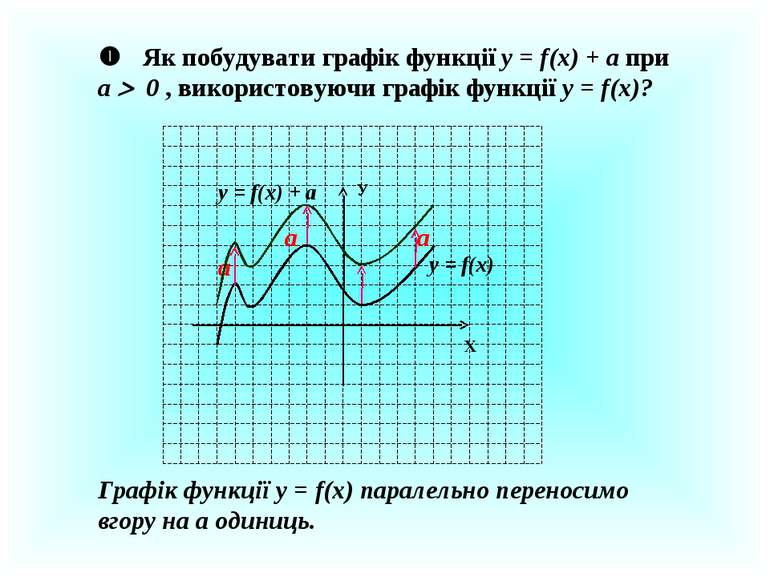
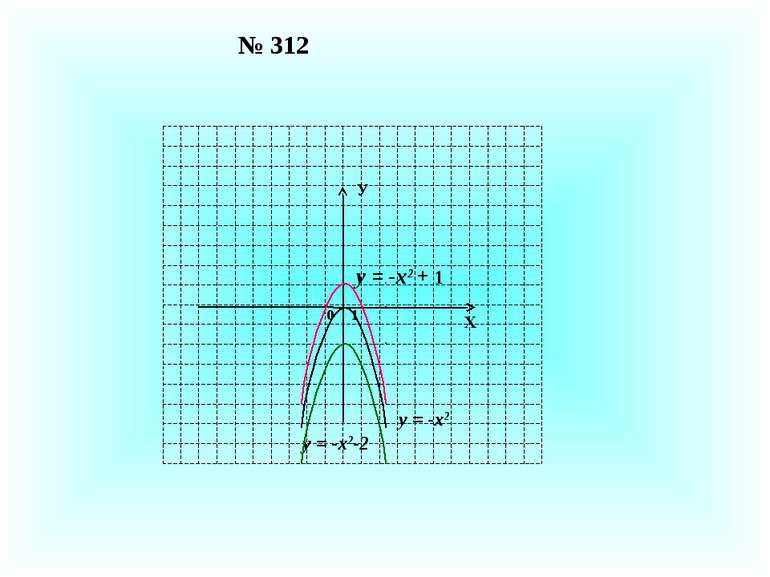
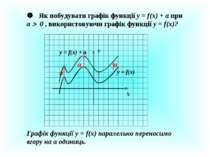
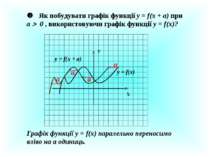
Як побудувати графік функції у = f(x) + a при a 0 , використовуючи графік функції у = f(x)? У Х у = f(x) a a a у = f(x) + а Графік функції у = f(x) паралельно переносимо вгору на а одиниць.

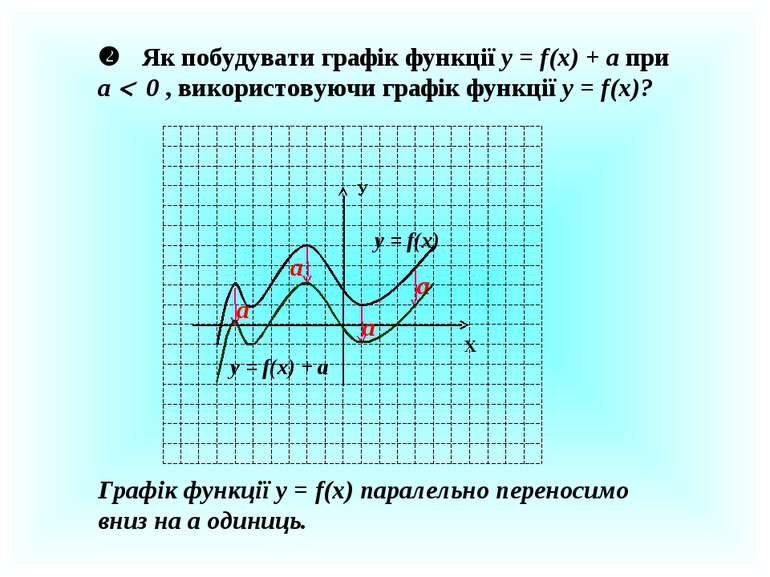
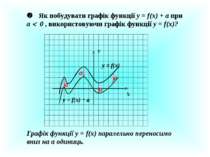
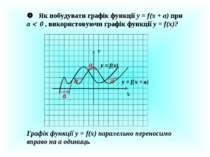
Як побудувати графік функції у = f(x) + a при a 0 , використовуючи графік функції у = f(x)? У Х у = f(x) a a a a у = f(x) + а Графік функції у = f(x) паралельно переносимо вниз на а одиниць.

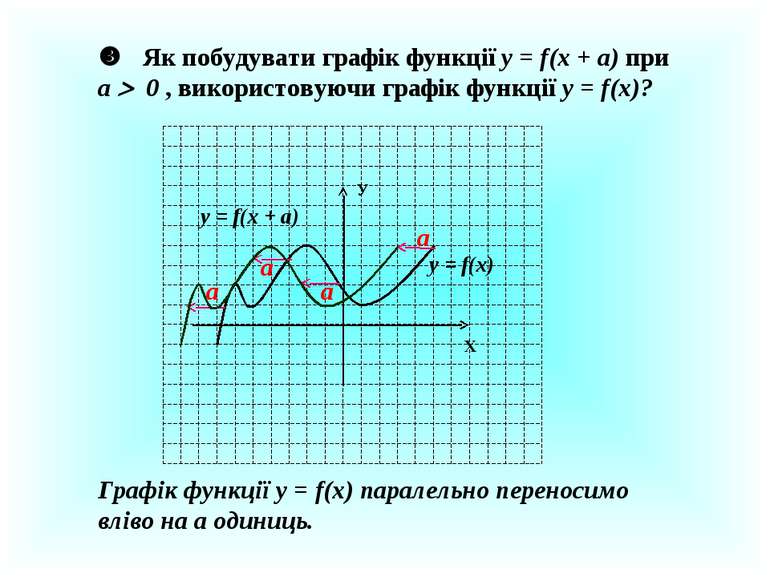
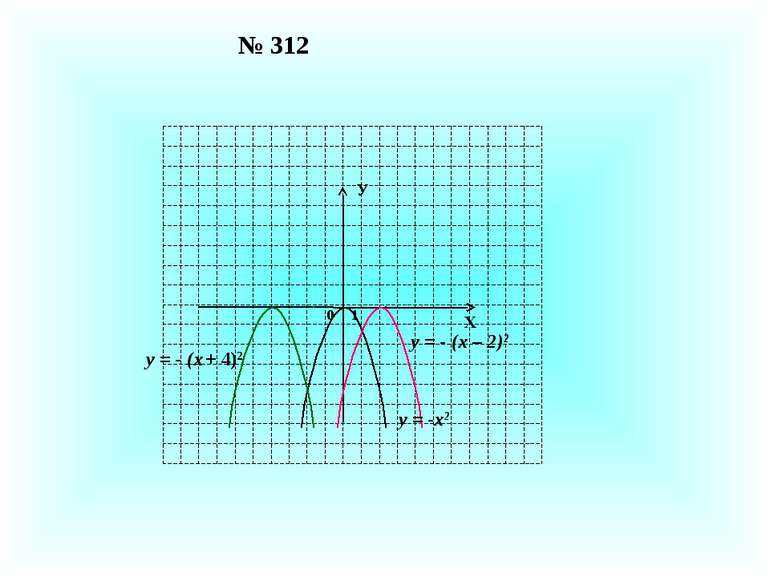
Як побудувати графік функції у = f(x + a) при a 0 , використовуючи графік функції у = f(x)? У Х у = f(x) a a a a у = f(x + а) Графік функції у = f(x) паралельно переносимо вліво на а одиниць.

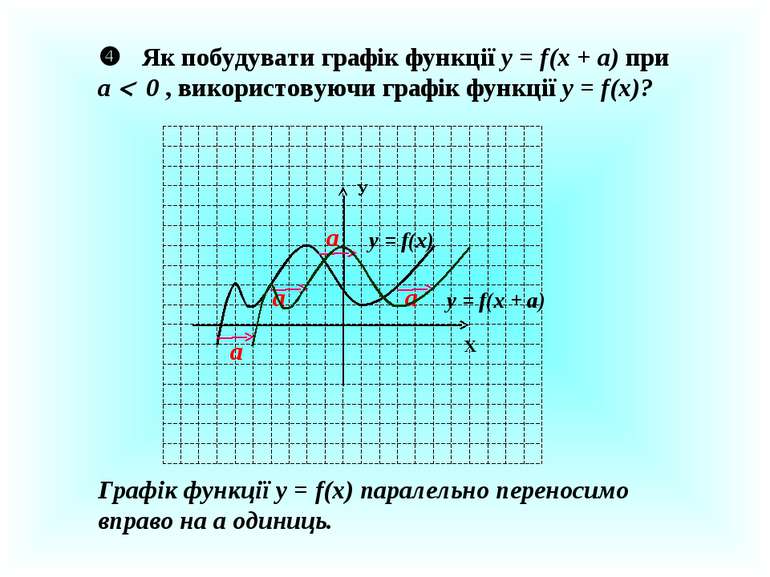
Як побудувати графік функції у = f(x + a) при a 0 , використовуючи графік функції у = f(x)? У Х у = f(x) a a a a у = f(x + а) Графік функції у = f(x) паралельно переносимо вправо на а одиниць.

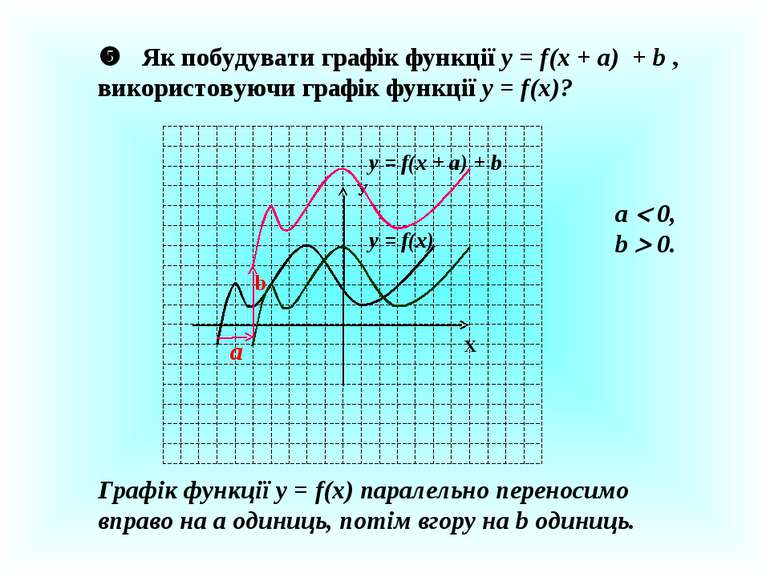
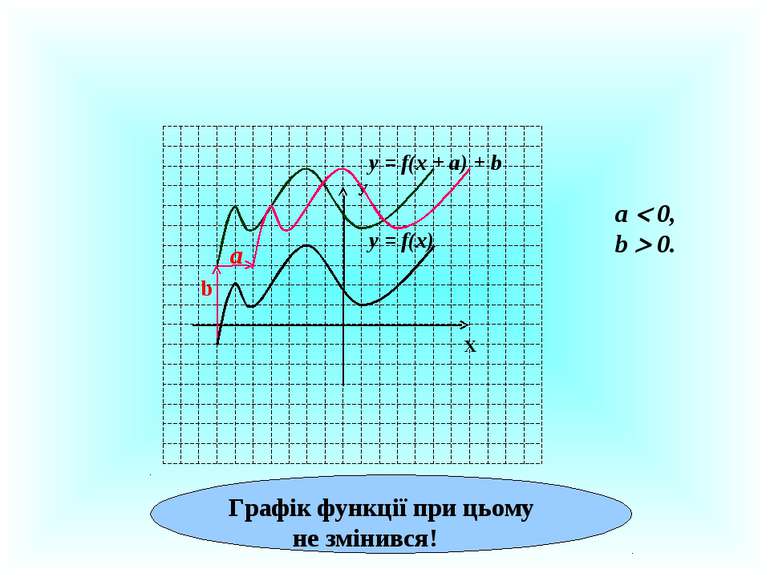
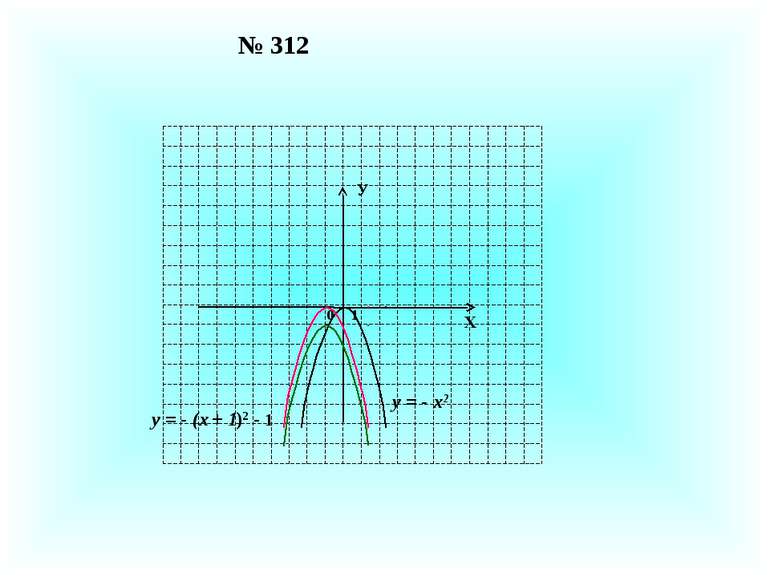
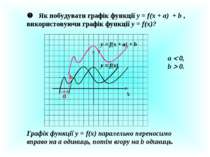
Як побудувати графік функції у = f(x + a) + b , використовуючи графік функції у = f(x)? У Х у = f(x) a у = f(x + а) + b Графік функції у = f(x) паралельно переносимо вправо на а одиниць, потім вгору на b одиниць. а 0, b 0. b

А якщо спочатку графік функції у = f(x) паралельно перенести вгору на b одиниць, потім вправо на а одиниць? Чи зміниться при цьому графік функції у = f(x + а) + b ?

У Х у = f(x) a у = f(x + а) + b а 0, b 0. b Графік функції при цьому не змінився!

У Х 0 1 № 312 у = -х2-2 у = -х2 + 1 у = -х2

У Х 0 1 № 312 у = - (х + 4)2 у = -х2 у = - (х – 2)2

У Х 0 1 № 312 у = - (х + 1)2 - 1 у = - х2

У Х 0 1 № 312 у = - (х - 3)2 + 4 у = - х2

Підсумок уроку

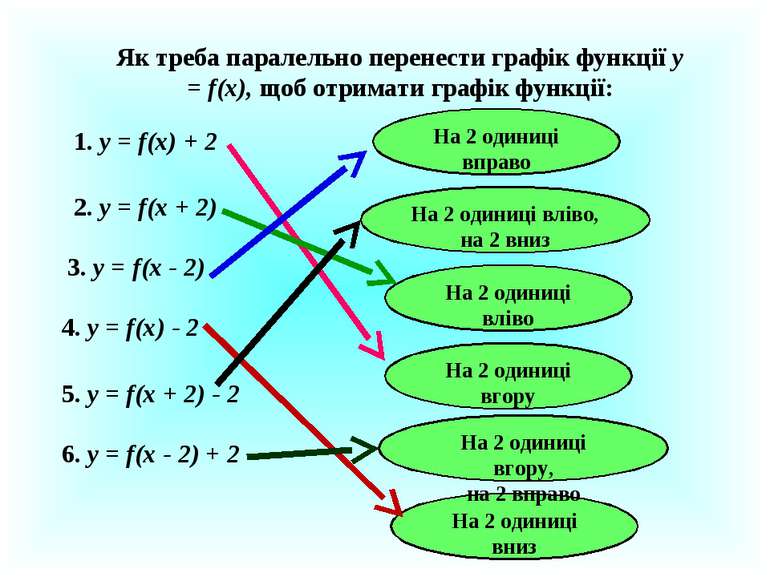
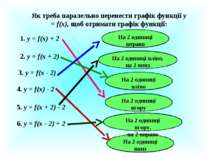
Як треба паралельно перенести графік функції у = f(x), щоб отримати графік функції: 1. у = f(x) + 2 2. у = f(x + 2) 3. у = f(x - 2) 4. у = f(x) - 2 5. у = f(x + 2) - 2 6. у = f(x - 2) + 2 На 2 одиниці вправо На 2 одиниці вниз На 2 одиниці вліво На 2 одиниці вгору На 2 одиниці вгору, на 2 вправо На 2 одиниці вліво, на 2 вниз

Домашнє завдання Вивчити п. 10, № 311, 314

Урок № 8

Щоб уникати помилок, необхідно набувати досвіду, щоб набувати досвіду, треба робити помилки. Л. Дж. Пітер

Тема уроку: Побудова графіків функцій Мета уроку: Формувати практичні навики побудови графіків функцій; розвивати графічну культуру, математичну мову; вміння аналізувати і співставляти, робити висновки

Тестові завдання

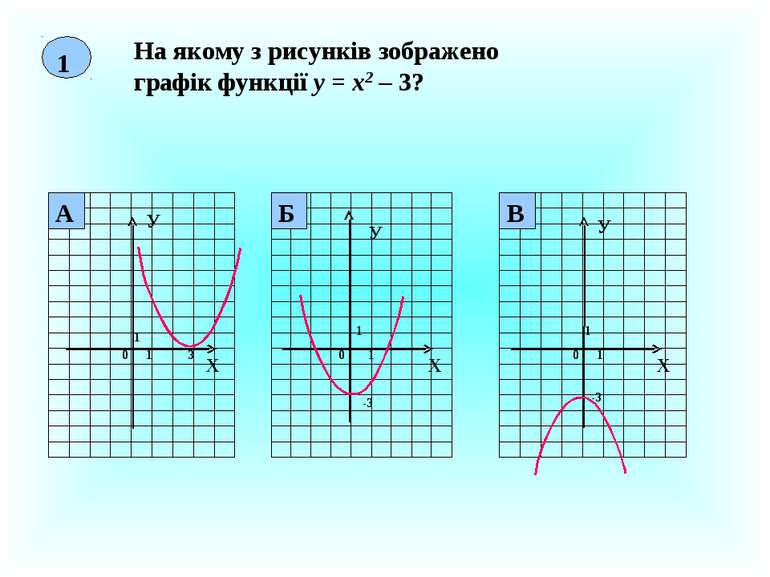
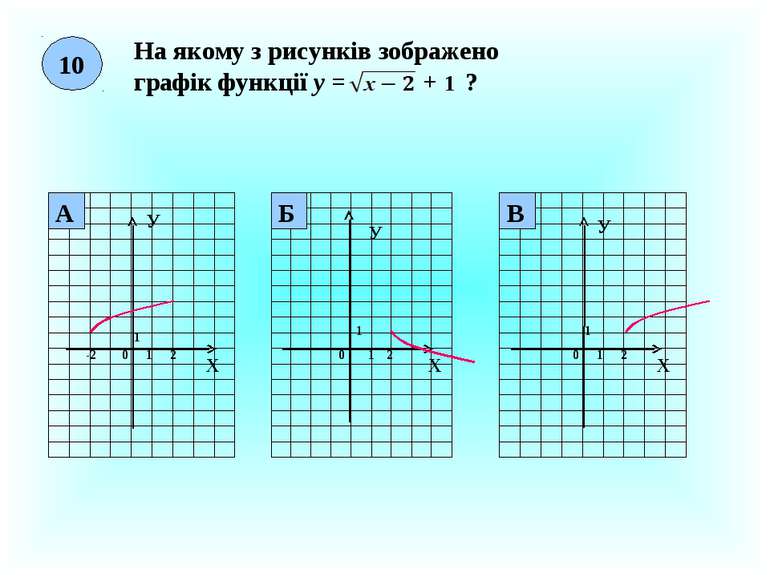
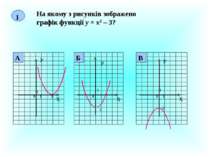
1 На якому з рисунків зображено графік функції у = х2 – 3? Х У 0 1 1 3 Х У 0 1 1 -3 Х У 1 1 0 -3 Б А В

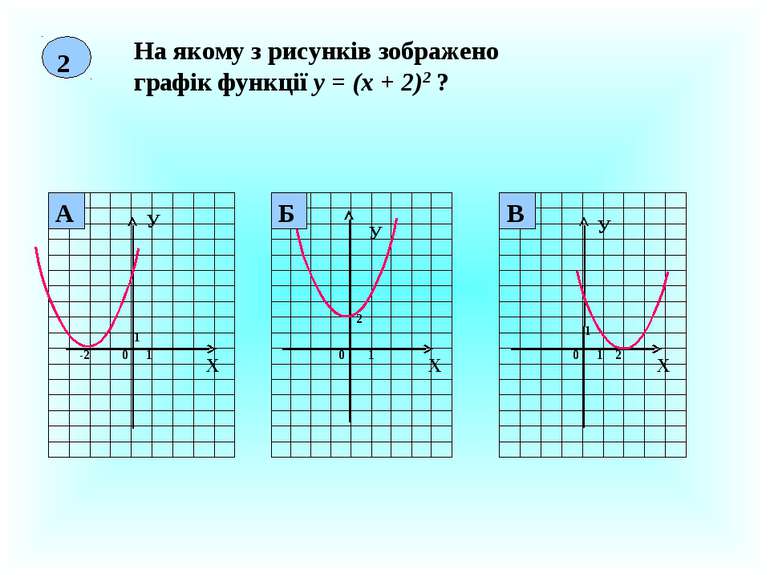
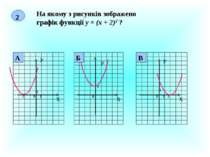
2 На якому з рисунків зображено графік функції у = (х + 2)2 ? Х У 0 1 1 -2 Х У 0 1 2 Х У 1 1 0 2 А Б В

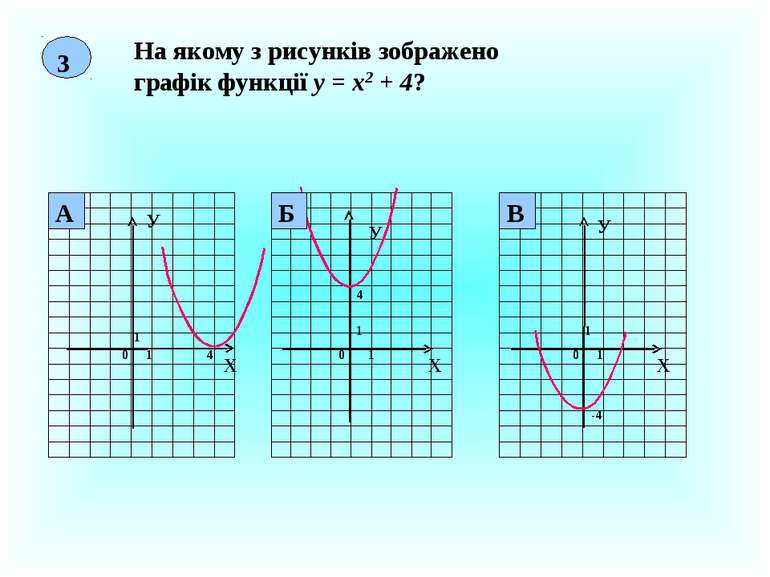
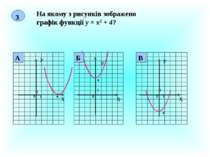
3 На якому з рисунків зображено графік функції у = х2 + 4? Х У 0 1 1 4 Х У 0 1 1 4 Х У 1 1 0 -4 Б А В

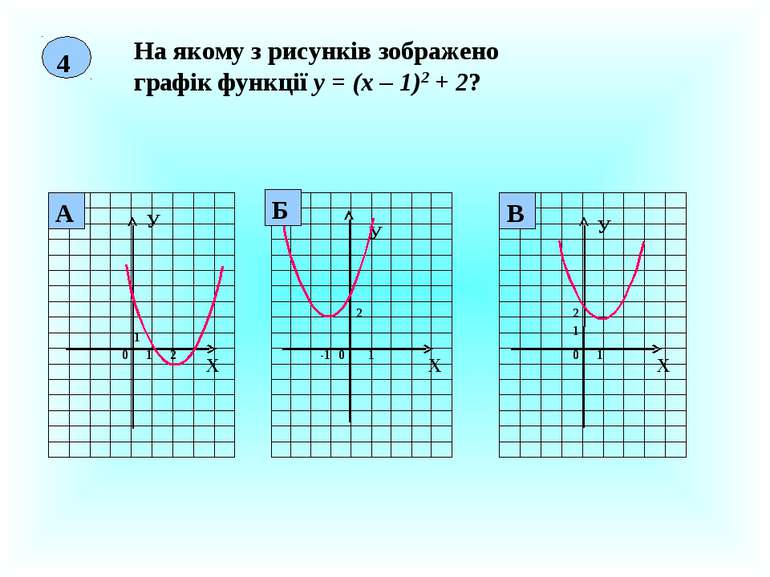
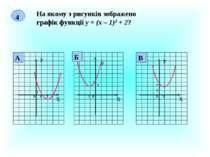
4 На якому з рисунків зображено графік функції у = (х – 1)2 + 2? Х У 0 1 1 2 Х У 0 1 2 -1 Х У 1 1 0 2 В Б А

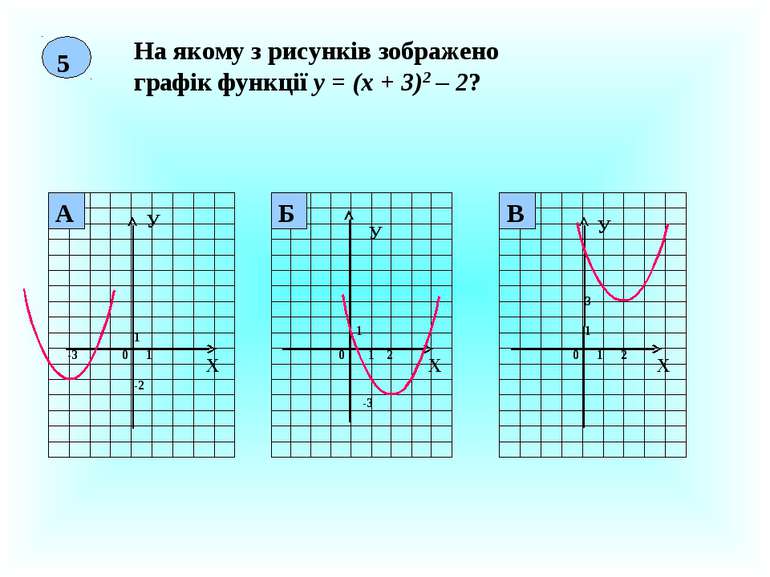
5 На якому з рисунків зображено графік функції у = (х + 3)2 – 2? Х У 0 1 1 -3 Х У 0 1 1 -3 Х У 1 1 0 3 А -2 2 2 Б В

6 На якому з рисунків зображено графік функції у = 1? Х У 0 1 1 3 Х У 0 1 1 -1 Х У 1 1 0 -1 В Б А

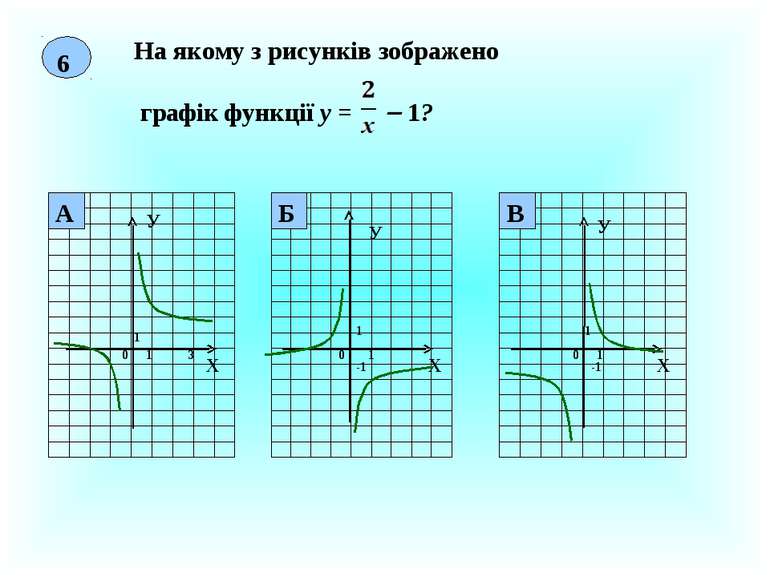
7 На якому з рисунків зображено графік функції у = ? Х У 0 1 1 3 Х У 0 1 1 -1 Х У 1 1 0 -1 В Б А -1

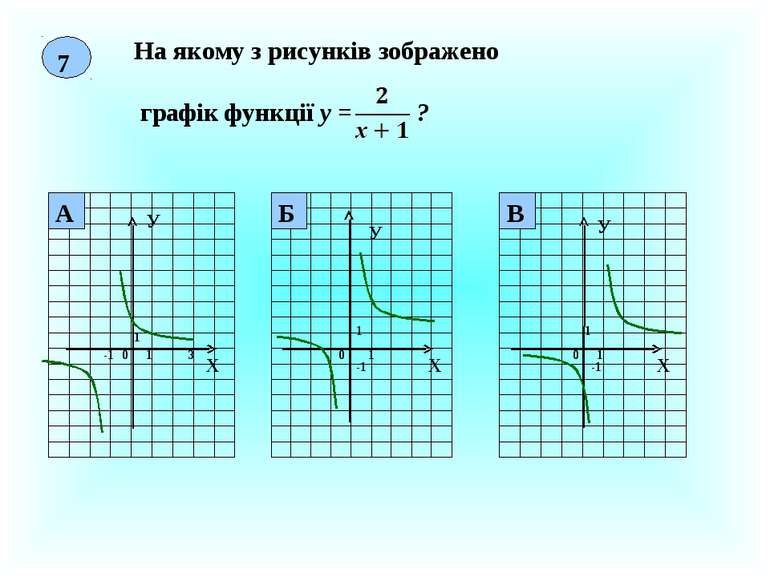
8 На якому з рисунків зображено графік функції у = ? Х У 0 1 1 3 Х У 0 1 1 -1 Х У 1 1 0 -1 В Б А -1 3 3 -3 3 -3 -3 3

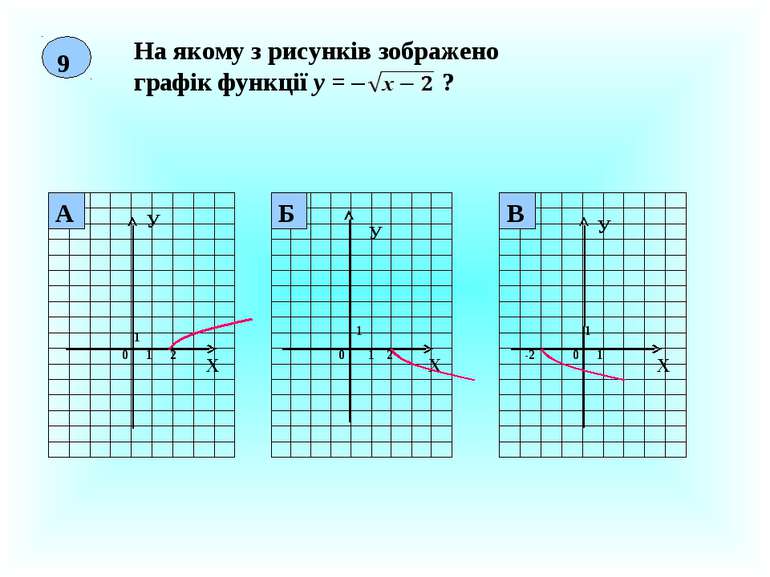
9 На якому з рисунків зображено графік функції у = – ? Х У 0 1 1 2 Х У 0 1 1 Х У 1 1 0 -2 Б 2 А В

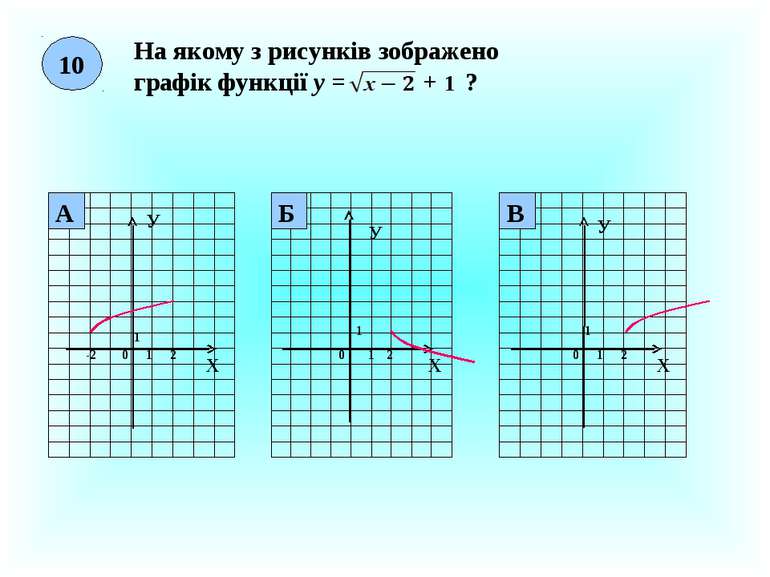
10 На якому з рисунків зображено графік функції у = + 1 ? Х У 0 1 1 2 Х У 0 1 1 Х У 1 1 0 Б 2 А В 2 -2

10 На якому з рисунків зображено графік функції у = + 1 ? Х У 0 1 1 2 Х У 0 1 1 Х У 1 1 0 Б 2 А В 2 -2

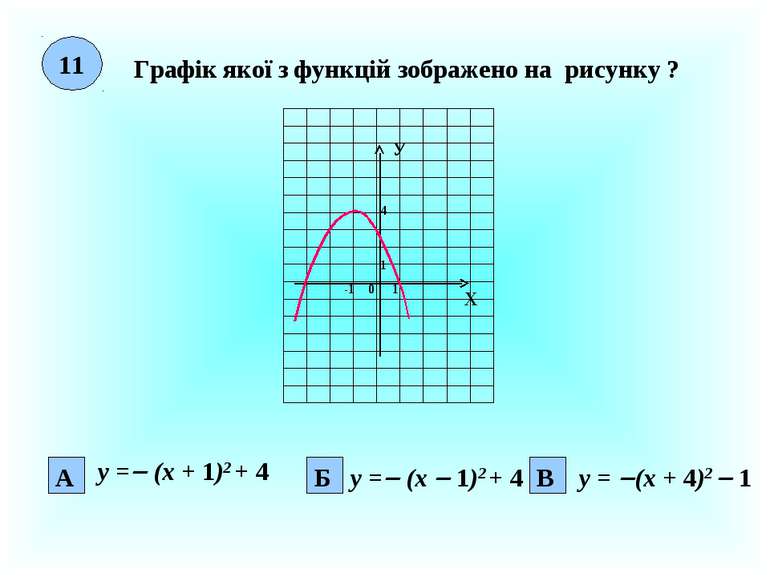
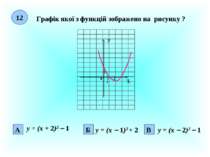
11 Графік якої з функцій зображено на рисунку ? Х У 0 1 1 4 А Б -1 В у = (х + 1)2 + 4 у = (х 1)2 + 4 у = (х + 4)2 1

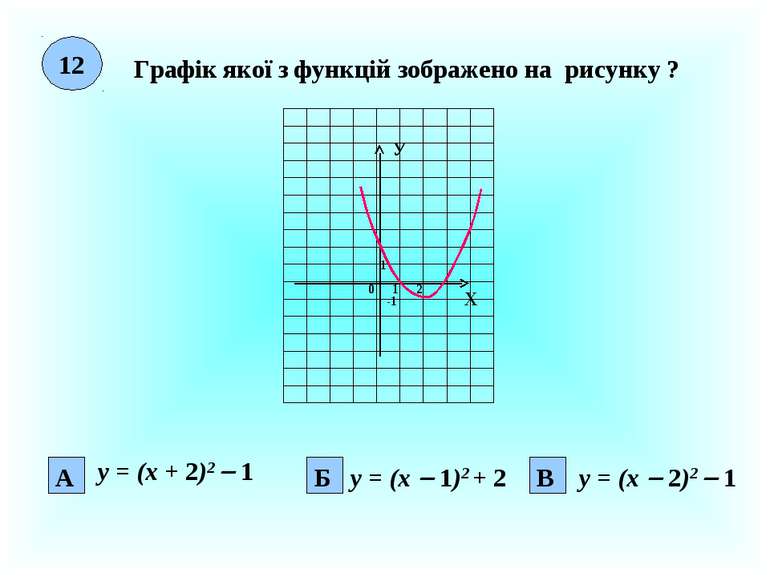
12 Графік якої з функцій зображено на рисунку ? Х У 0 1 1 2 А Б -1 В у = (х + 2)2 1 у = (х 1)2 + 2 у = (х 2)2 1

“Акваріум”

Розв’яжіть графічно рівняння (х – 1)2 = Х У 0 1 у=(х – 1)2 2 у =

Розв’яжіть графічно рівняння 1 – х2 = Х У 0 0,5 у= 1 – х2 2 1 у =

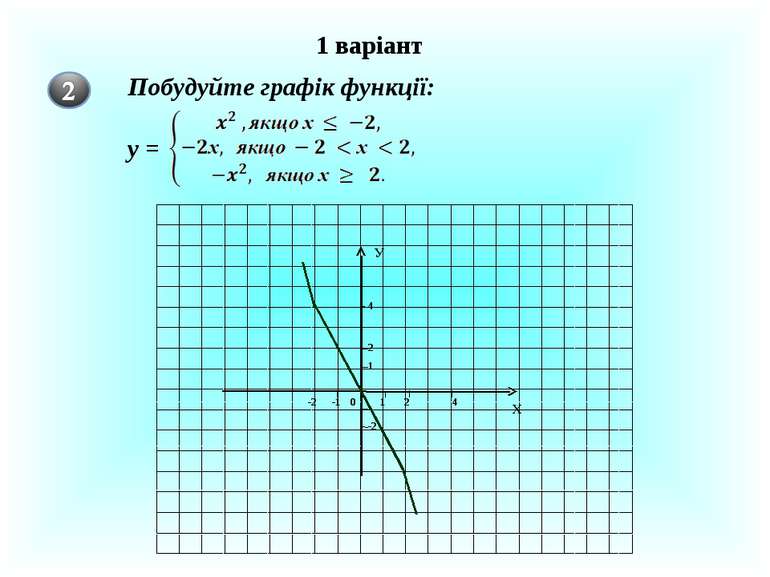
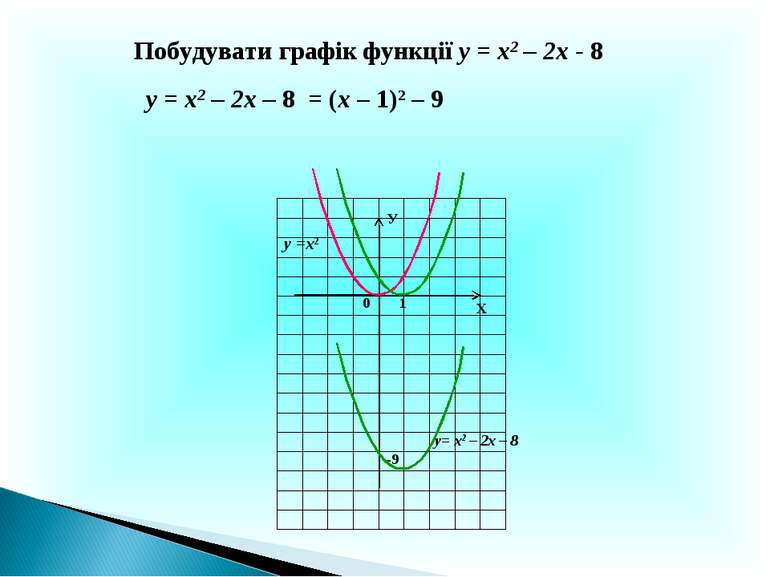
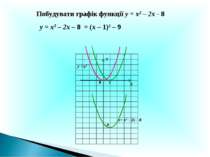
Х У 0 у= х2 – 2х – 8 1 Побудувати графік функції у = х2 – 2х - 8 -9 у = х2 – 2х – 8 = (х – 1)2 – 9 у =х2

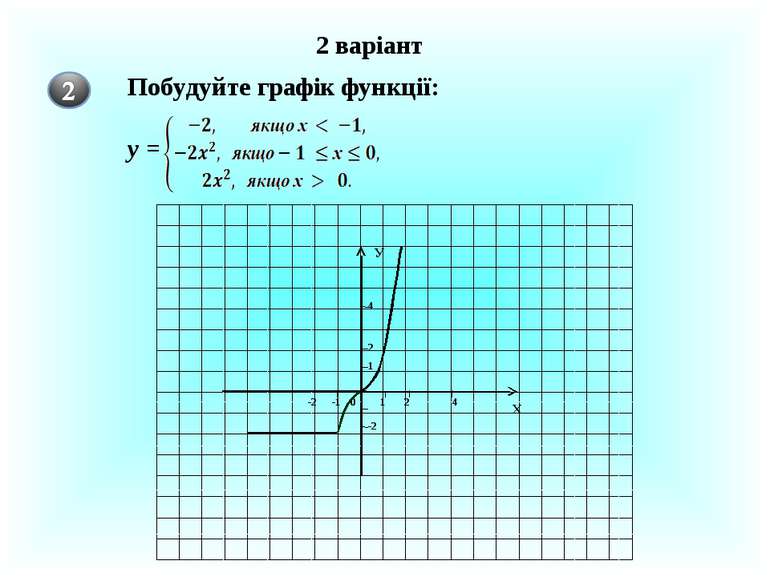
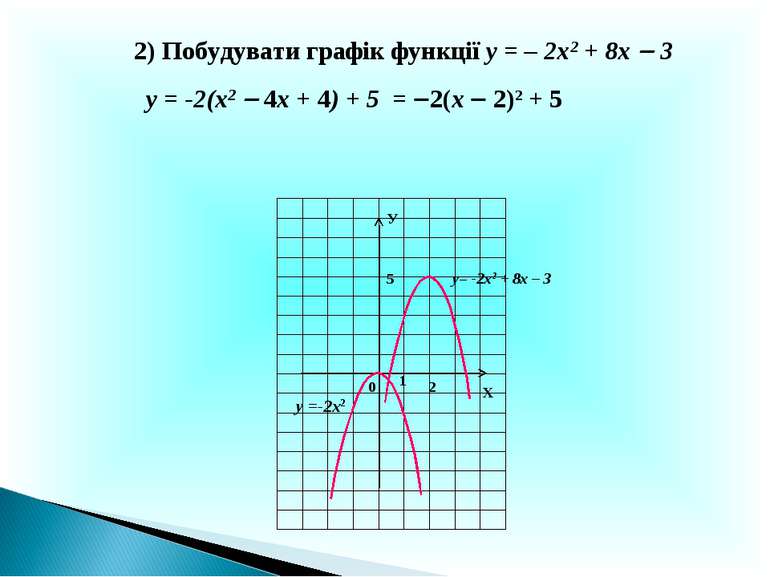
Х У 0 у= -2х2 + 8х – 3 1 2) Побудувати графік функції у = – 2х2 + 8х 3 у = -2(х2 4х + 4) + 5 = 2(х 2)2 + 5 у =-2х2 2 5

Підсумок уроку

Домашнє завдання Повторити п. 9-10 № 325, 330

Урок № 9

Знання збираються по краплині, як вода в долині. Прислів’я

Тема уроку: Квадратична функція, її графік і властивості Мета уроку: Ввести поняття квадратичної функції; розглянути способи побудови її графіка; розвивати логічне мислення; вміння самостійно працювати

Перевірка домашнього завдання

№ 325 Розв’язати графічно рівняння = + 2 Х У 0 1 2 у = + 2 у = х = 1

№ 330 Побудувати графік функції у = Х У 0 1 -1 4

Означення: Функцію, яку можна задати формулою виду у = ах2 + bх + с, де х – незалежна змінна, а, b, с – деякі числа, причому а ≠ 0, називають квадратичною.

Побудова графіка квадратичної функції

1. Виділення квадрата двочлена у = ах2 + bx + c = а = a = a x0 = - , y0 = (x0; y0) – координати вершини параболи.

2. Побудова графіка за схемою А. Визначаємо напрям віток параболи в залежності від значення а. Б. Знаходимо абсцису вершини параболи за формулою х0 = - . В. Знаходимо ординату вершини параболи, підставивши значення х0 в умову. Г. Знаходимо точки перетину графіка з віссю абсцис, розв’язавши рівняння у = 0. Д. Знаходимо точку перетину графіка з віссю ординат. Е. Будуємо графік, сполучаючи точки.

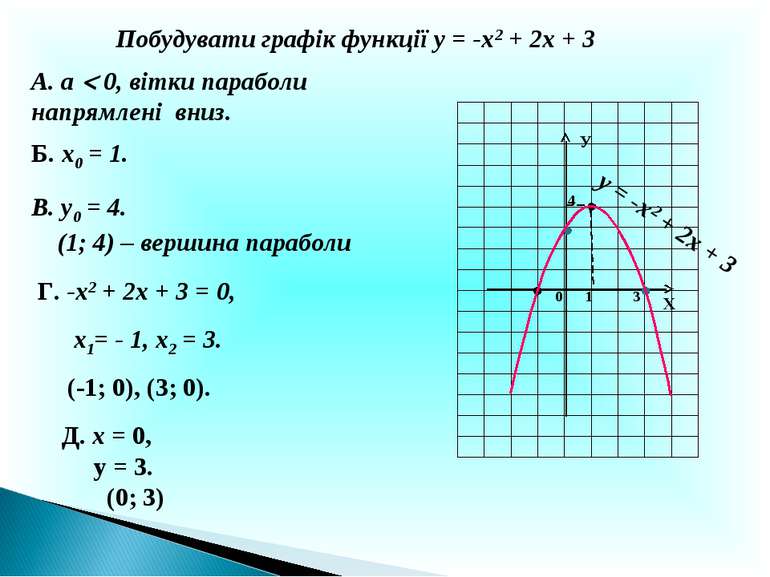
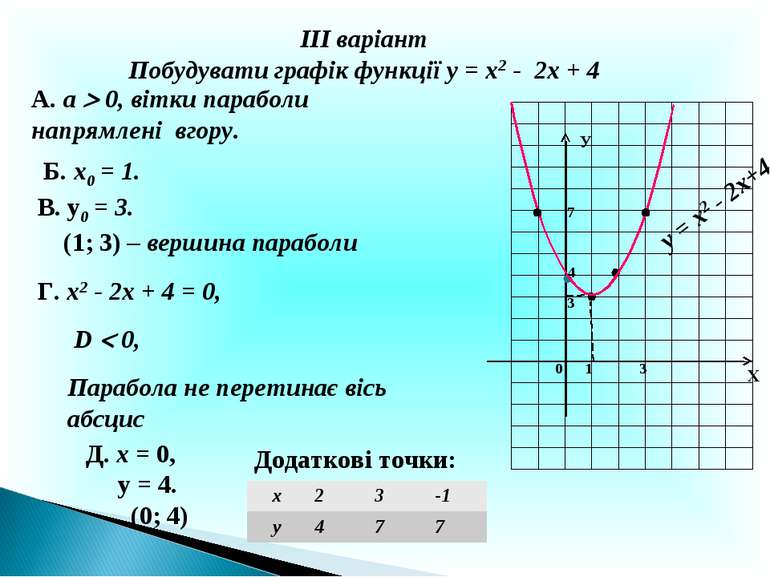
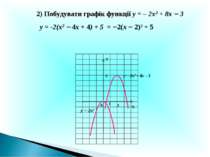
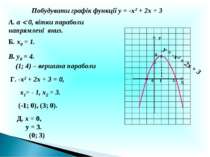
Побудувати графік функції у = -х2 + 2х + 3 А. а 0, вітки параболи напрямлені вниз. Б. х0 = 1. В. у0 = 4. (1; 4) – вершина параболи Г. -х2 + 2х + 3 = 0, х1= - 1, х2 = 3. (-1; 0), (3; 0). Д. х = 0, у = 3. (0; 3) Х У 1 0 4 3 у = -х2 + 2х + 3

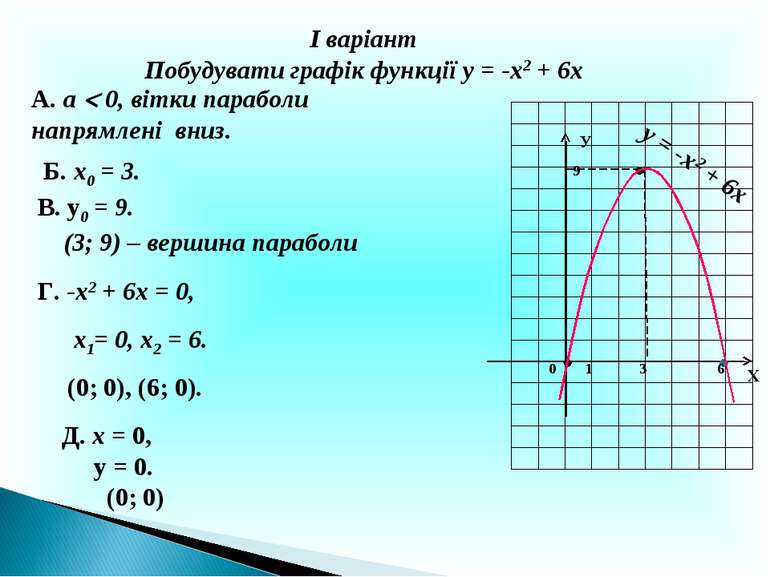
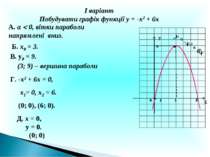
І варіант Побудувати графік функції у = -х2 + 6х А. а 0, вітки параболи напрямлені вниз. Б. х0 = 3. В. у0 = 9. (3; 9) – вершина параболи Г. -х2 + 6х = 0, х1= 0, х2 = 6. (0; 0), (6; 0). Д. х = 0, у = 0. (0; 0) Х У 9 3 у = -х2 + 6х 1 0 6

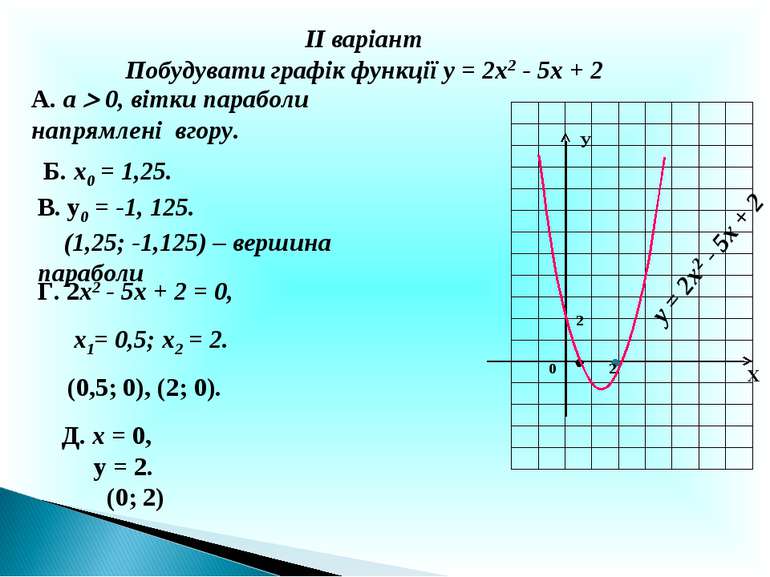
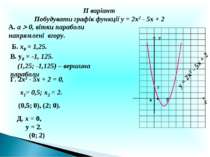
ІІ варіант Побудувати графік функції у = 2х2 - 5х + 2 А. а 0, вітки параболи напрямлені вгору. Б. х0 = 1,25. В. у0 = -1, 125. (1,25; -1,125) – вершина параболи Г. 2х2 - 5х + 2 = 0, х1= 0,5; х2 = 2. (0,5; 0), (2; 0). Д. х = 0, у = 2. (0; 2) Х У 2 у = 2х2 - 5х + 2 0 2

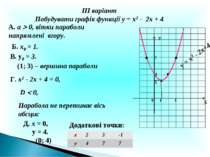
ІІІ варіант Побудувати графік функції у = х2 - 2х + 4 А. а 0, вітки параболи напрямлені вгору. Б. х0 = 1. В. у0 = 3. (1; 3) – вершина параболи Г. х2 - 2х + 4 = 0, D 0, Парабола не перетинає вісь абсцис Д. х = 0, у = 4. (0; 4) Х У 3 у = х2 - 2х+4 1 0 4 Додаткові точки: 3 7 х 2 3 -1 у 4 7 7

“Інтелектуальна розминка” Зобразіть схематично графік функції у = ах2 + bх + с , якщо:

1) а 0, D 0, c 0, - 0 X У X У X У А Б В

2) а 0, D = 0, - 0. X У X У X У А Б В

3) а 0, D 0, - 0. X У X У X У А Б В

4) а 0, с = 0, - 0. X У X У X У А Б В

Підсумок уроку

Вивчити п.11, № 341(1; 3), 349 Домашнє завдання

Урок № 10

Математика – наука молодих. Інакше й не може бути. Заняття математикою – це така гімнастика розуму, для якої потрібна вся гнучкість і вся витривалість молодості. Н. Вінер

Тема уроку: Функції і їх властивості Мета уроку: Систематизувати здобуті знання; розвивати логічне мислення; вміння працювати самостійно і в команді

І команда 1. Графіком лінійної функції є пряма. 2. Функція, яку можна задати формулою у = ах2 + bх + с, де а ≠ 0, х – змінна, а, b, с – числа, називається квадратичною. 3. Найменше значення функції у = ах2, де а 0, дорівнює нулю. 4. Множиною значень функції у = х2 + 1 є проміжок 1; +∞ ). 5. Вершина параболи у = 2х2 – 4х + 5 знаходиться в точці (1; 3). 6. Щоб отримати графік функції у = (х + 4)2 переносимо графік функції у = х2 паралельно вліво.

ІІ команда 1. Графіком функції обернена пропорційність є гіпербола. 2. Функція, яку можна задати формулою у = kх, де k ≠ 0, називається прямою пропорційністю. 3. Областю визначення квадратичної функції є ( ∞; +∞). 4. Найбільше значення функції у = -4х2 дорівнює нулю. 5. Вершина параболи у = 3х2 + 6х 1 знаходиться в точці ( 1; 4). 6. Щоб отримати графік функції у = х2 – 3 переносимо графік функції у = х2 паралельно вниз.

Знайдіть область визначення даних функції і розшифруйте вислів. у = у = у = у = у = у =

( ∞; 2), (2; +∞ ) х R х 5 х 4 х 4 ( ∞; 2), ( 2; 2), (2; + ∞)

Щоб перетравити знання, потрібно поглинати їх з апетитом. А. Франс

Молодці!

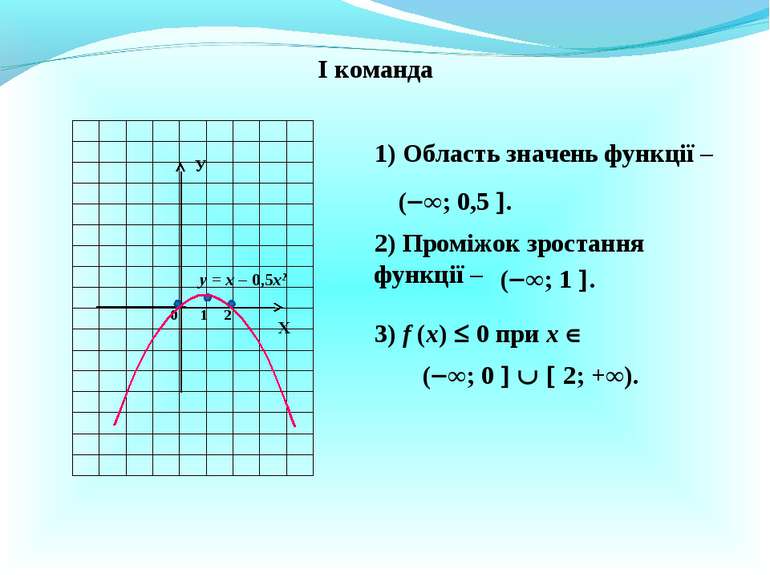
І команда у = х – 0,5х2 Х У 0 1 2 1) Область значень функції – ( ∞; 0,5 . 2) Проміжок зростання функції – ( ∞; 1 . 3) f (x) 0 при х ( ∞; 0 2; +∞).

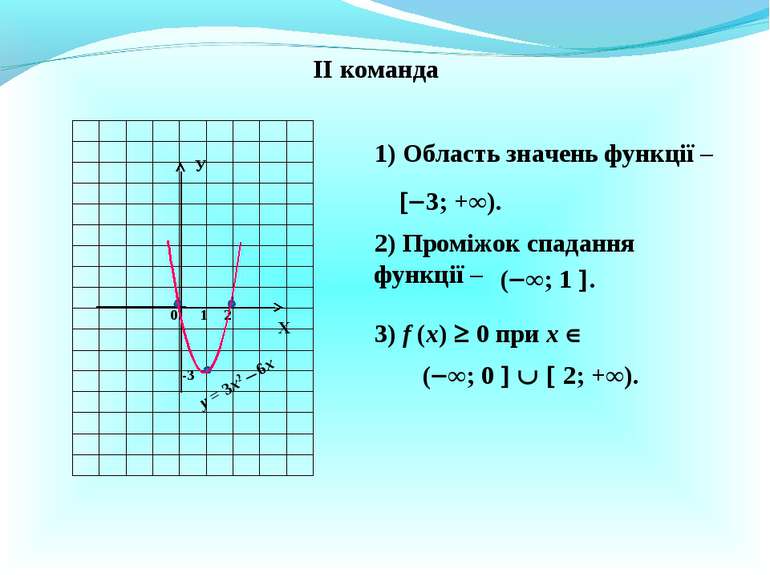
ІІ команда у = 3х2 6х Х У 0 1 2 1) Область значень функції – 3; +∞). 2) Проміжок спадання функції – ( ∞; 1 . 3) f (x) 0 при х ( ∞; 0 2; +∞). -3

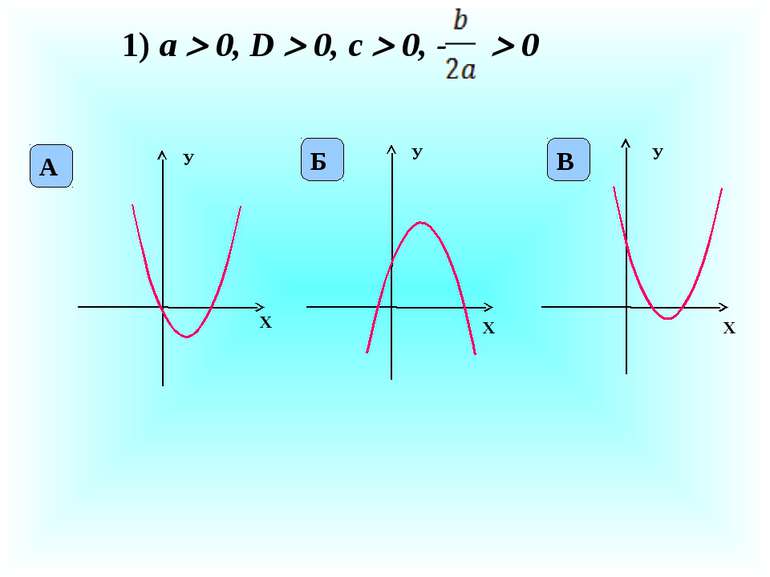
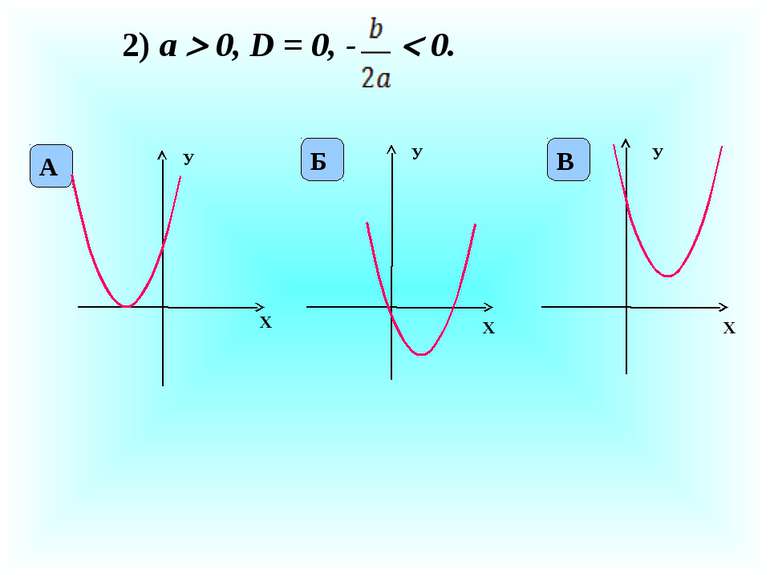
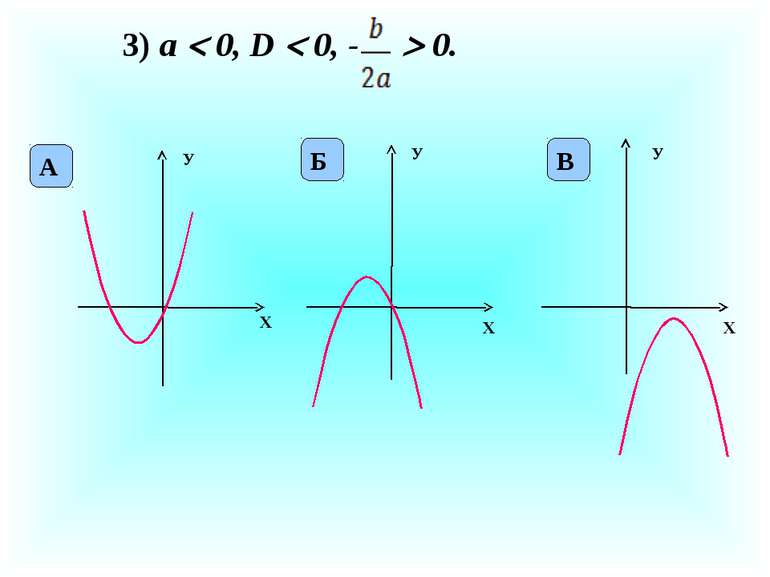
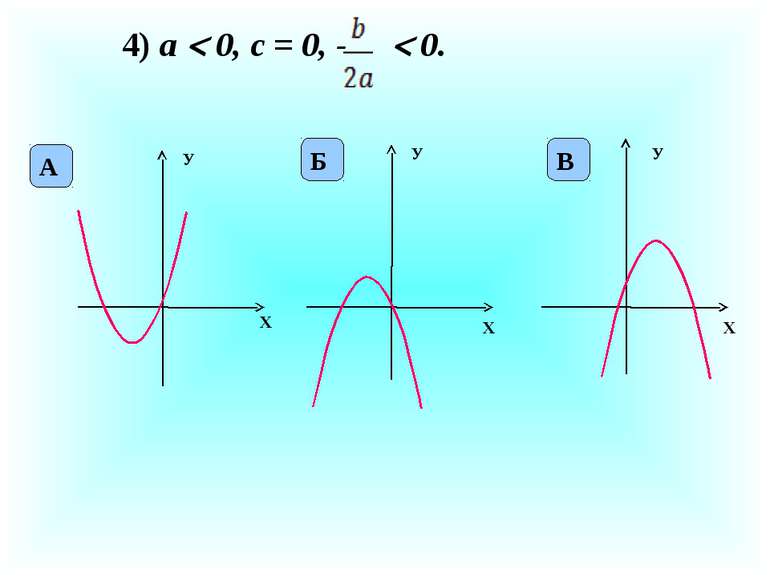
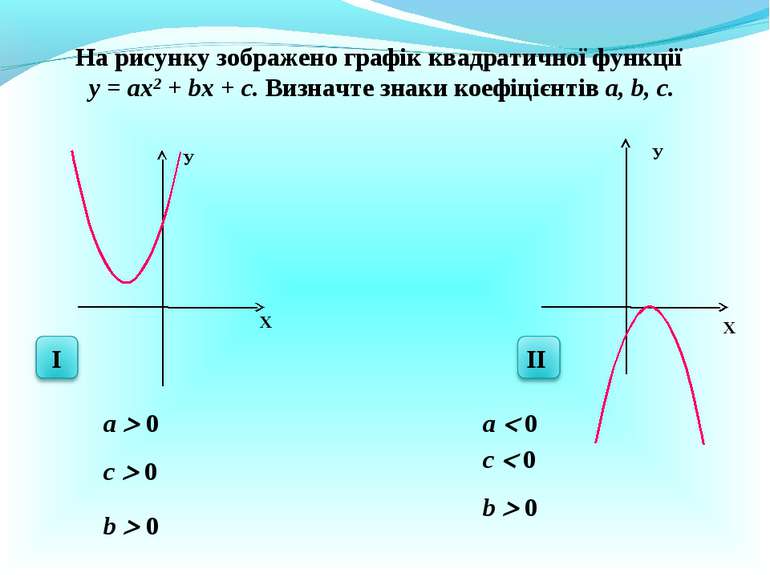
X У X У На рисунку зображено графік квадратичної функції у = ах2 + bх + с. Визначте знаки коефіцієнтів а, b, с. а 0 с 0 b 0 а 0 с 0 b 0

Не будуючи графіків функцій, знайти найменше значення функцій:

“За одного битого двох небитих дають” у = 2х Х У

“Униз вода знесе, вгору вітер винесе” у = х2 Х У

МОЛОДЦІ!

Дякую за урок!

Те, що я встиг пізнати, чудово. Сподіваюся, таке ж чудове те, що мені доведеться пізнати. Сократ

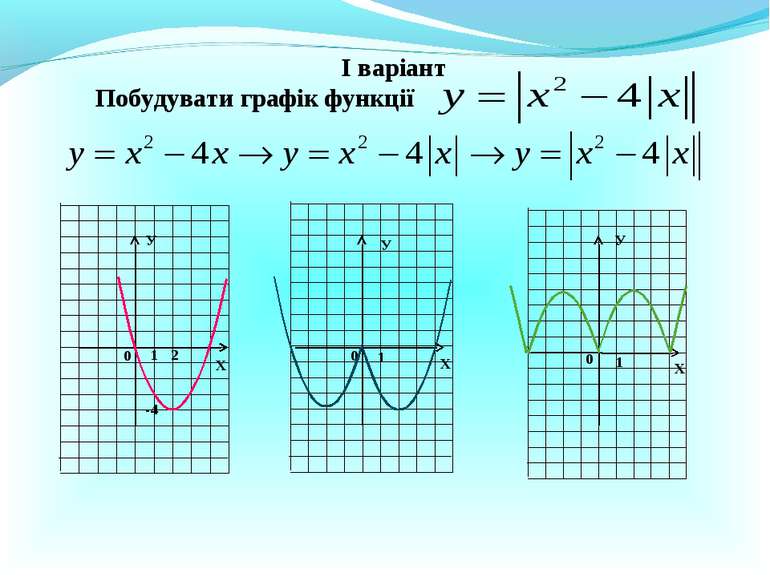
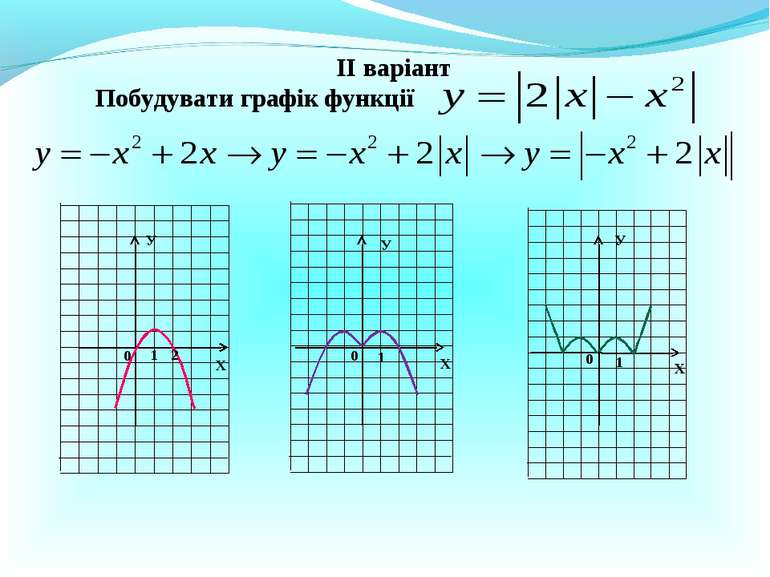
Тема уроку: Побудова графіків функцій, що містять модуль Мета уроку: Навчитися будувати графіки функцій, що містять модуль, використовуючи перетворення; формувати графічну культуру; вміння спостерігати і аналізувати

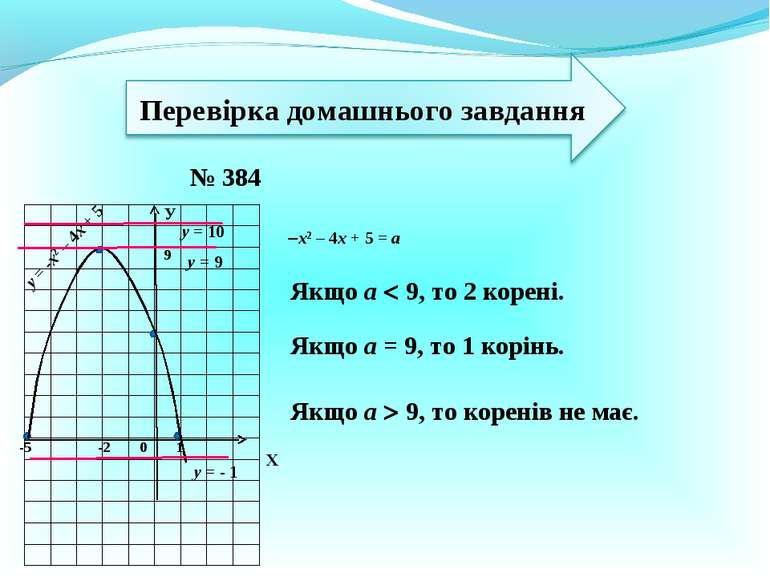
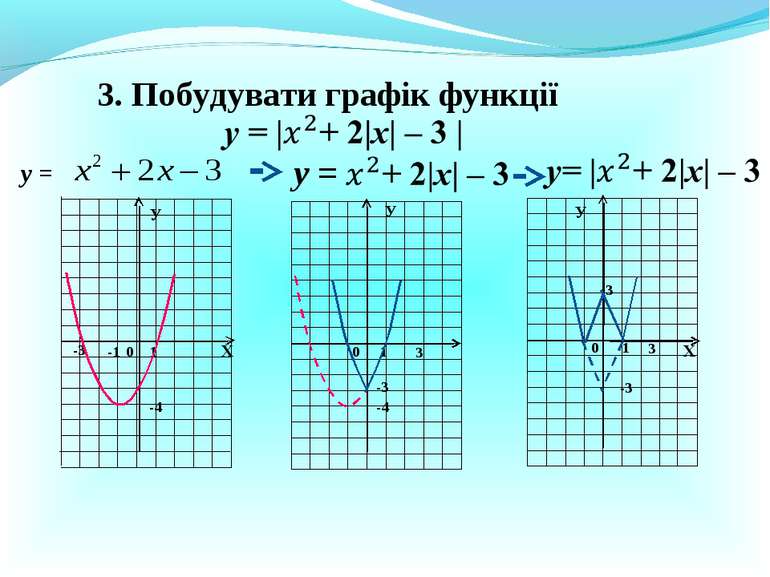
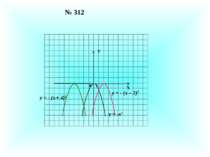
№ 384 Х У 0 1 -2 9 -5 у = -х2 – 4х + 5 у = - 1 у = 9 у = 10 х2 – 4х + 5 = а Якщо а 9, то 2 корені. Якщо а = 9, то 1 корінь. Якщо а 9, то коренів не має.

Спростіть вирази: , якщо х 2; А) х 4; Б) х; В) х + 4; Г) х 4. 1) 3 5 = А) 8; Б) 2; В) 2; Г) 8. 2) 6 8 = А) 2; Б) 14; В) 14; Г) 2. 3) x 2x = , якщо х 0; А) 3х; Б) х; В) х; Г) 3х. 4) 2 – х + 2, якщо х 2; А) 4 – х; Б) х; В) х + 4; Г) х – 4. 5) 1 2 3 4 5 В Г А Б А

Чи правильно побудовано графік функції у = |f (x)| ? Х У 0 1

Означення модуля: f (x) = f (x), якщо f (x) 0, f (x), якщо f (x) 0.

1. Графік функції у = f (x) Х У Х У у = f (x) у = | f (x) | (х; - у) (х; у)

2. Графік функції у = f ( x ) Х У Х У у = f (x) у = f (|x|) У Х

3. Графік функції у = f (-x) Х У у = f (x) у = f (-x) У Х (х; у) (-х; у)

1. Побудувати графік функції у = | х – 3 | у = х – 3 у = | х – 3 | Х Х У У 0 1 3 -3 0 1 3

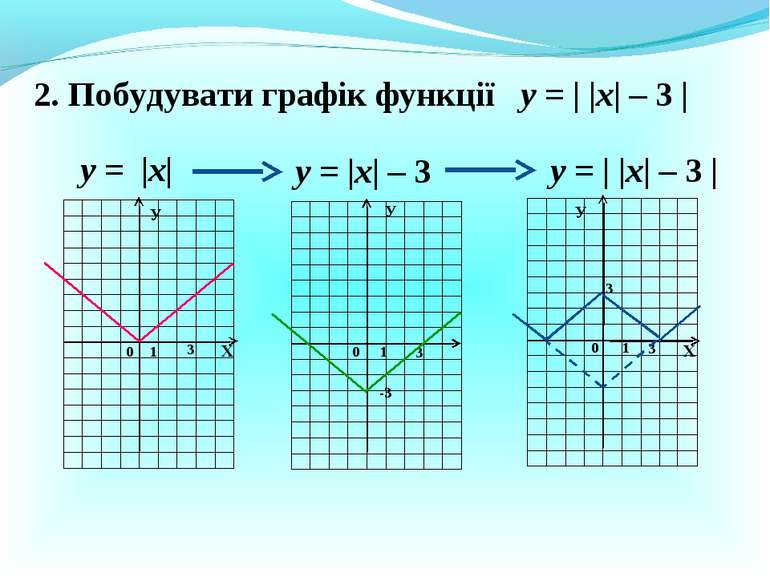
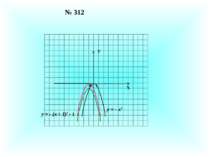
2. Побудувати графік функції у = |х| у = |х| – 3 Х Х У У 0 1 3 -3 0 1 3 у = | |х| – 3 | у = | |х| – 3 | 0 1 3 У 3

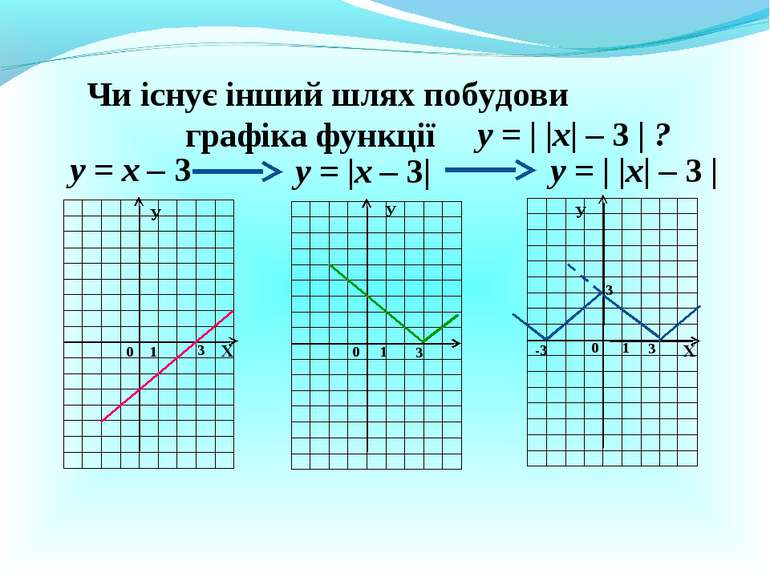
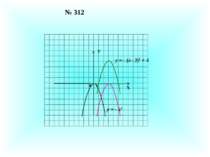
Чи існує інший шлях побудови графіка функції у = х – 3 у = |х – 3| Х Х У У 0 1 3 0 1 3 у = | |х| – 3 | у = | |х| – 3 | ? 0 1 3 У -3 3

3. Побудувати графік функції у = Х Х У У 0 1 -3 0 1 3 0 1 3 У 3 у = -1 -4 -4 -3 -3

4. Побудувати графік функції → → → Х Х Х Х У У У У 1 0 0 0 0 1 1 1 4 4 4 2 2 -2

5. Побудувати графіки функції І варіант ІІ варіант

І варіант Побудувати графік функції Х Х Х У У У 0 1 0 0 1 1 2 -4

ІІ варіант Побудувати графік функції Х Х Х У У У 0 1 0 0 1 1 2