Презентація на тему:
Фігурні числа

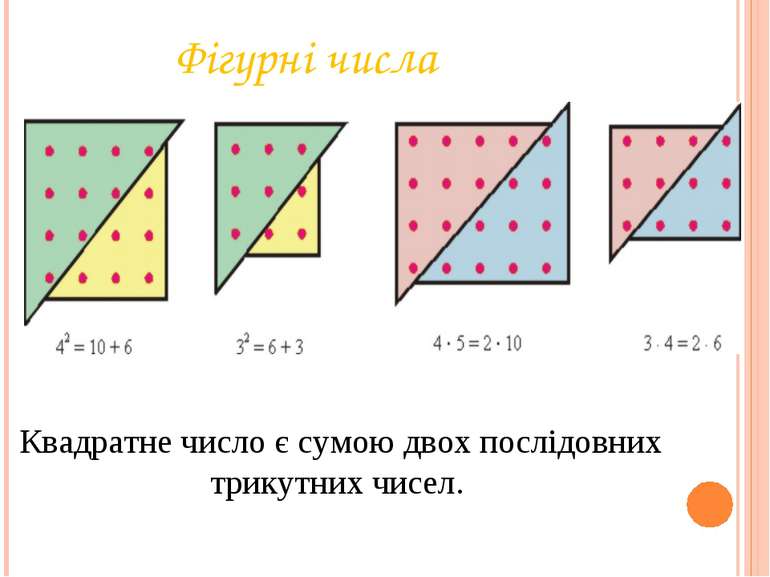
ФІГУРНІ ЧИСЛА материал подготовлен для сайта matematika. ukoz. com

1. Види фігурних чисел: А) лінійні, Б) плоскі, В) телесні, Г) многокутні. 2. Фігурні числа і трикутник Паскаля. материал подготовлен для сайта matematika. ukoz. com

Фігурні числа Фигу рні чи сла — загальна назва чисел, пов'язаних з тією або іншою геометричною фігурою . Припускають, що вперше вони з'явилися в VI столітті до нашої ери - у школі Піфагора. Надалі багато математиків цікавилися цими числами.

Фигурні числа Згідно піфагорійскому вченню, в основі світу лежать числа ( натуральні ) . З цих міркувань арифметика піфагорійців була тісно пов'язана з геометрією : вони виділяли класи чисел, що мають одну і ту ж форму, а саме: трикутні, квадратні , п'ятикутні  і так далі. Числа стародавніми греками, а разом з ними Піфагором і піфагорійцями мислилися зримо, у вигляді камінчиків , розкладених на піску або на лічильної дошці - абаці . З цієї причини греки не знали нуля , тому що його неможливо було "побачити" .

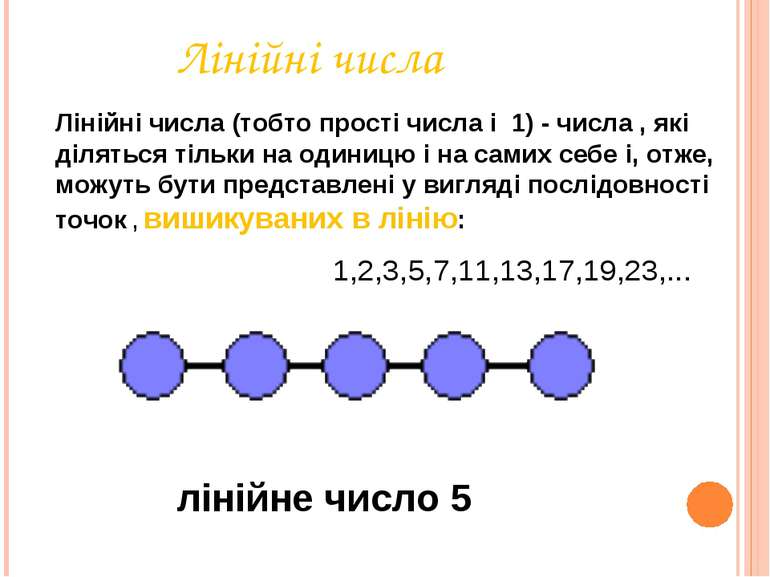
Лінійні числа Лінійні числа (тобто прості числа і 1) - числа , які діляться тільки на одиницю і на самих себе і, отже, можуть бути представлені у вигляді послідовності точок , вишикуваних в лінію: лінійне число 5 1,2,3,5,7,11,13,17,19,23,...

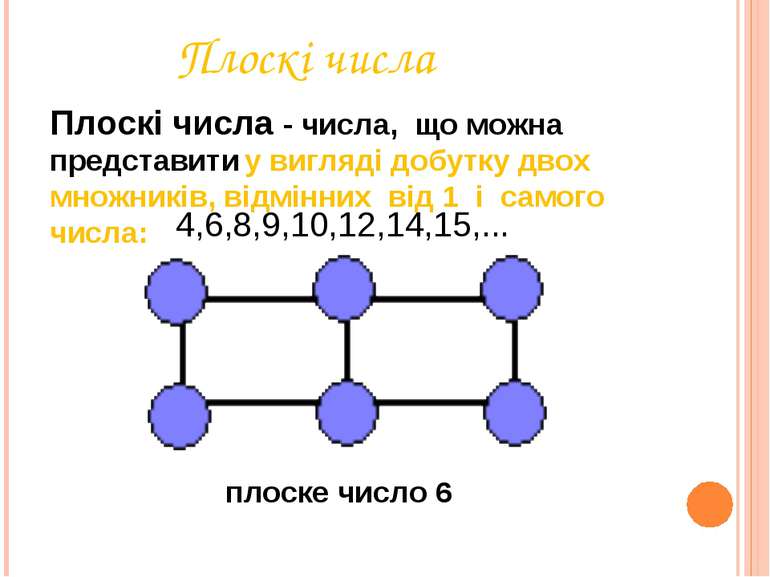
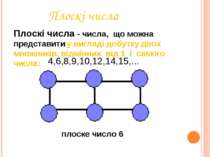
Плоскі числа Плоскі числа - числа, що можна представити у вигляді добутку двох множників, відмінних від 1 і самого числа: плоске число 6 4,6,8,9,10,12,14,15,...

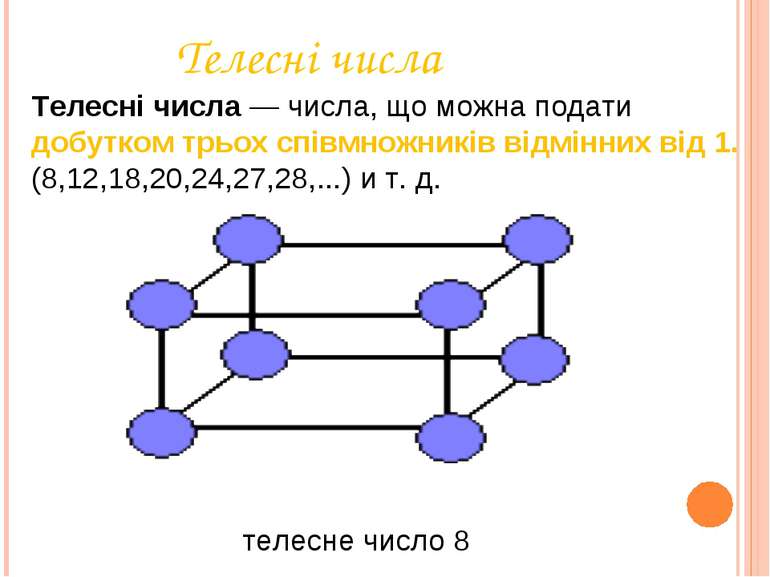
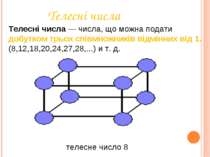
Телесні числа Телесні числа — числа, що можна подати добутком трьох співмножників відмінних від 1. (8,12,18,20,24,27,28,...) и т. д. телесне число 8

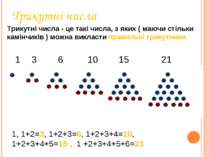
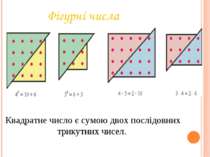
Трикутні числа Трикутні числа - це такі числа, з яких ( маючи стільки камінчиків ) можна викласти правильні трикутники. 1 3 6 10 15 21 1, 1+2=3, 1+2+3=6, 1+2+3+4=10, 1+2+3+4+5=15 , 1 +2+3+4+5+6=21

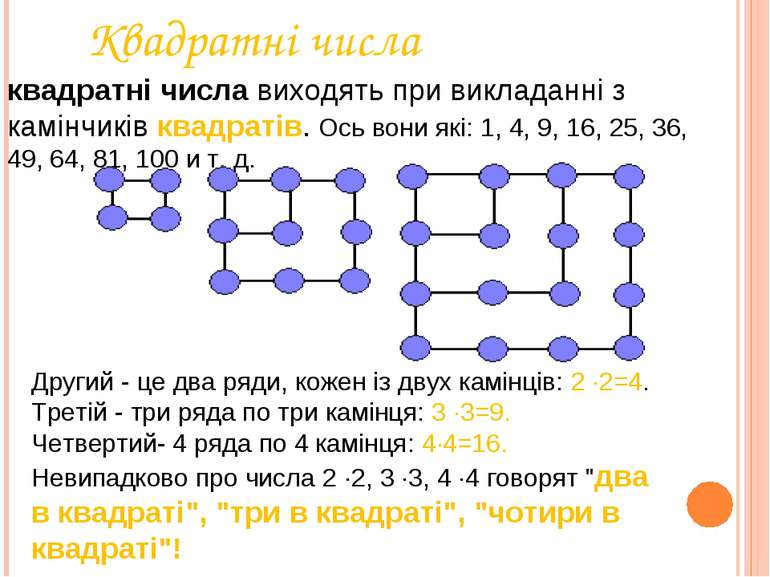
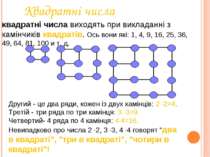
Квадратні числа квадратні числа виходять при викладанні з камінчиків квадратів. Ось вони які: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 и т. д. Другий - це два ряди, кожен із двух камінців: 2 ·2=4. Третій - три ряда по три камінця: 3 ·3=9. Четвертий- 4 ряда по 4 камінця: 4·4=16. Невипадково про числа 2 ·2, 3 ·3, 4 ·4 говорят "два в квадраті", "три в квадраті", "чотири в квадраті"!

П’ятикутні числа Можна розглядати і шестикутні, і семикутні числа, і взагалі , числа , що виникають при складанні різноманітних багатокутників , з різними  сторонами або з однаковими .

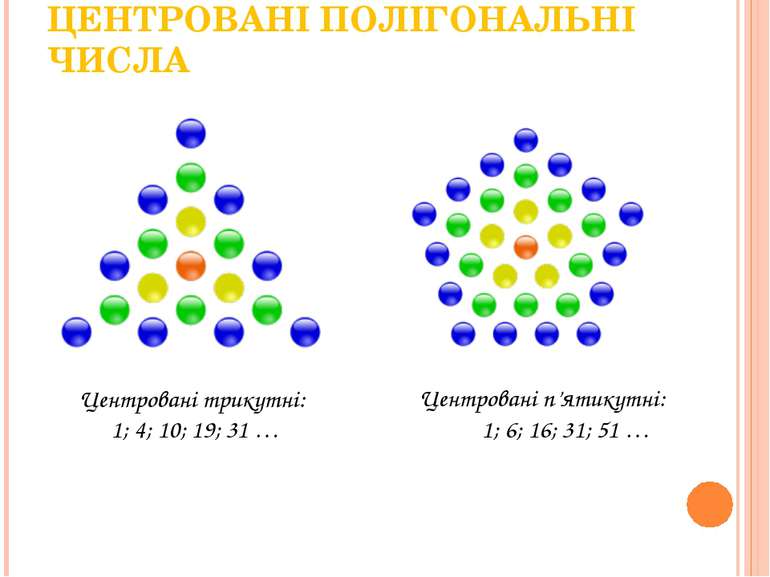
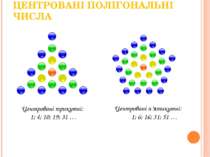
ЦЕНТРОВАНІ ПОЛІГОНАЛЬНІ ЧИСЛА Центровані трикутні: 1; 4; 10; 19; 31 … Центровані п’ятикутні: 1; 6; 16; 31; 51 … материал подготовлен для сайта matematika. ukoz. com

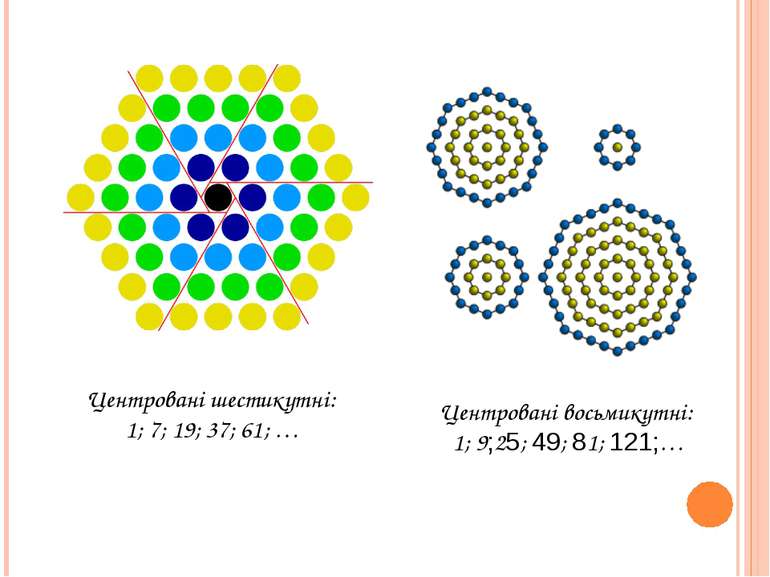
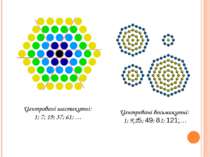
Центровані шестикутні: 1; 7; 19; 37; 61; … Центровані восьмикутні: 1; 9;25; 49; 81; 121;… материал подготовлен для сайта matematika. ukoz. com

Кубічні числа Дуже цікаві кубічні числа, що виникають при складанні кубиків: 1, 2 · 2 · 2 =8(два поверхи із квадратів 2 ·2). 3·3·3=27 (три поверхи із квадратів 3·3) 4·4·4=64 (чотири поверхи із квадратів 4·4) 5·5·5=125, 6·6·6=216, 7·7·7=343, 8·8·8=512, 9·9·9=729, 10·10·10= 1000 і так далі. Тепер зрозуміло, чому про такі числа говорять: "два в кубі", "три в кубі", "десять в кубі"?

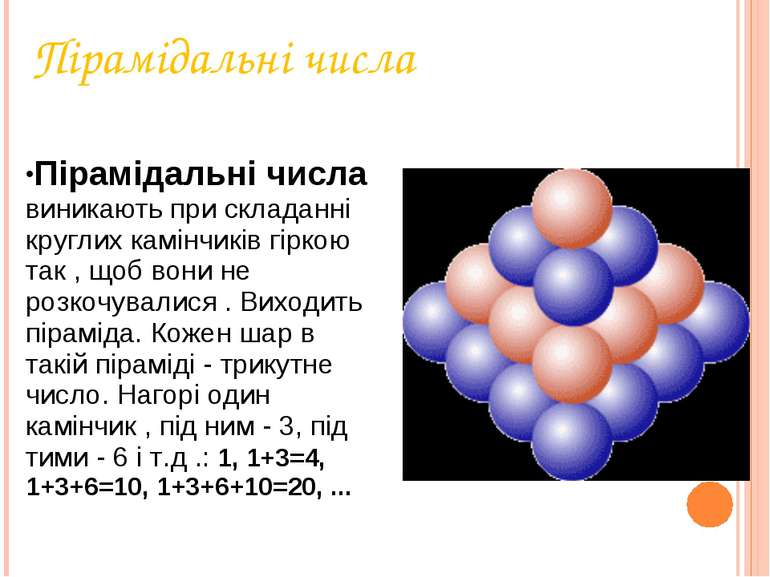
Пірамідальні числа Пірамідальні числа виникають при складанні круглих камінчиків гіркою так , щоб вони не розкочувалися . Виходить піраміда. Кожен шар в такій піраміді - трикутне число. Нагорі один камінчик , під ним - 3, під тими - 6 і т.д .: 1, 1+3=4, 1+3+6=10, 1+3+6+10=20, ...

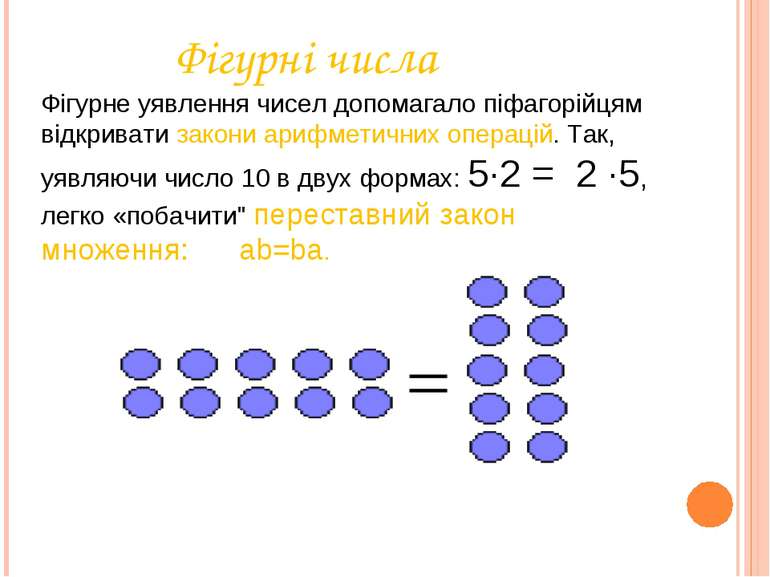
Фігурні числа Фігурне уявлення чисел допомагало піфагорійцям відкривати закони арифметичних операцій. Так, уявляючи число 10 в двух формах: 5·2 = 2 ·5, легко «побачити" переставний закон множення: ab=ba.

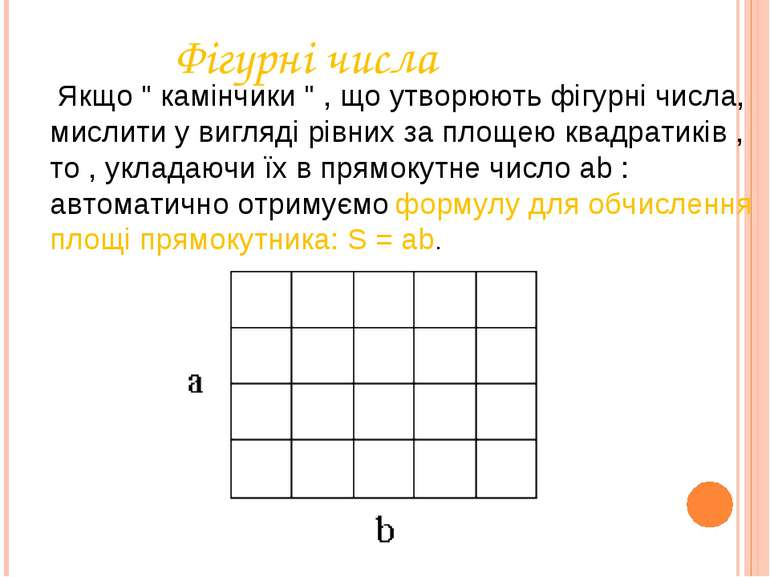
Фігурні числа Якщо " камінчики " , що утворюють фігурні числа, мислити у вигляді рівних за площею квадратиків , то , укладаючи їх в прямокутне число ab : автоматично отримуємо формулу для обчислення площі прямокутника: S = ab.

Фігурні числа У Новий час багатокутними числами займалися Ферма , Ейлер , Гаус та інші. Ферма сформулював ( 1637 р.) так звану «золоту теорему » : Всяке натуральне число - або трикутне або сума двох або трьох трикутних чисел; Всяке натуральне число - або квадратне , або сума двох , трьох або чотирьох квадратних чисел; Всяке натуральне число - або п'ятикутне , або сума від двох до п'яти п'ятикутних чисел : і тощо. Цією теоремою займалися багато видатних математиків , повний доказ зумів дати  Коші в 1813 році.

Фігурні числа  Квадратне число є сумою двох послідовних трикутних чисел.

Фігурні числа Рахунок на камінцях залишив глибокий слід в історії математики. Стародавні греки, коли їм доводилося множити числа, малювали прямокутники ; результатом множення трьох на п'ять був прямокутник зі сторонами три і п'ять. Це- розвиток рахунку на камінцях . Безліч закономірностей , що виникають при діях з числами , були виявлені давньогрецькими вченими при вивченні і кресленні . І довгі століття кращим підтвердженням справедливості таких співвідношень вважався спосіб геометричний , з прямокутниками , квадратами , пірамідами і кубами .

Фігурні числа Навіть у XVII століттi, коли була вже добре розвинена алгебра з позначеннями величин буквами , зі знаками дій , багато хто вважав її варварською наукою , придатною для низинних цілей- побутових розрахунків , допоміжних обчислень, - але ніяк не для благородних наукових праць. Один із видатних математиків того часу, Бонавентура Кавальєрі , користувався алгеброю , бо обчислювати з її допомогою простіше, але для обґрунтування своїх наукових результатів всі алгебраїчні викладки заміняв міркуваннями з  геометричними фігурами.

Фігурні числа Чому числа 2·2·2·2=16, 3·3·3·3=81, 4·4·4·4=256 і т.д. не мають своєї назви, хоча у квадратів і кубів чисел такі назви є? А справа в тому , що ми живемо в світі трьох вимірів (довжина, ширина и висота). Квадрат вийшов, коли ми виклали фігуру з однаковою довжиною і шириною : куб - фігура з однаковими довжиною , шириною і висотою. Але нема четвертого виміру, щоб викласти таку ж красиву фігуру із 2·2·2·2 камінців.

ФІГУРНІ ЧИСЛА І ТРИКУТНИК ПАСКАЛЯ У європейських математиків фігурними числами називали коефіцієнти членів степенів бінома (а + b)*, де * = 1, 2, 3, 4, … (а + b)¹ = 1а +1b, (а + b)² = 1а² + 2ab + 1b², (а + b)³ = 1a³ + 3a²b + 3ab² + 1b³, і т.д. Складемо таблицю : материал подготовлен для сайта matematika. ukoz. com

Перший стовпець і перший рядок представлений 0, 1, 1, 1, 1,… Другий стовпець і другий рядок – є натуральний ряд. Решта чисел таблиці, наприклад, 15 і 20, - суми чисел, що стоять у тому ж рядку ліворуч і в тому ж стовпці над шуканим числом: 15 = 10 + 5, 20 = 10 +10 тощо. За скісними лініями стоять коефіцієнти степенів (а + b). Ця таблиця була у Стифеля в 1544 році, у Паскаля – в 1665 році. У Німеччині його називають трикутником Стифеля, в Італії – трикутником Тартальї. Такий числовий трикутник є і у Омара Хаяма. Індійські історики математики (зокрема Сінгх А. Н.) стверджують, що числовий трикутник був відомий в Індії ще у ІІ ст. до н.е. і що про це у ІХ ст. написав Махавіра. Він рекомендує скласти числовий трикутник у такий спосіб. 1 материал подготовлен для сайта matematika. ukoz. com

Складають трикутник з клітинок, спочатку креслять одну клітинку, під нею – дві, щоб половини клітинок виступали з-під першої. Потім креслять три клітинки, щоб знову половини їх клітинок виступали з-під клітинок другого ряду, тощо. У крайні ліві і праві клітинки кожного ряду вписують одиницы, у кожну іншу клітинку вписують суму чисел, що стоять у двох клітинках над нею. Така побудова числового трикутника є зручнішою, ніж описаний вище спосіб Паскаля. У курсі алгебри числовий трикутник є корисним практичним посібником для складання послідовності коефіцієнтів членів розгорнутого виразу (а + b)*, при різних значеннях *. материал подготовлен для сайта matematika. ukoz. com

Дякую за увагу! материал подготовлен для сайта matematika. ukoz. com