Презентація на тему:
Дійсні числа та обчислення

Дійсні числа та обчислення Урок №1 10 клас Стандартний рівень Матеріал узагальнила вчитель математики Шельпахівської ЗОШ І-ІІІ ступенів Христинівського району Марченко Тамара Степанівна -8

Усе впорядковується відповідно до чисел ПІФАГОР САМОСЬКИЙ (бл. 580–500 рр. до н. е.)

R R

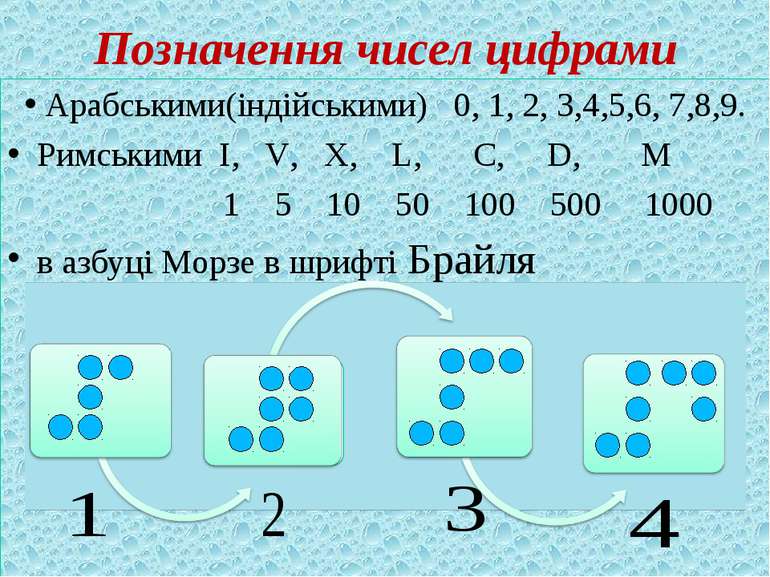
Позначення чисел цифрами Арабськими(індійськими) 0, 1, 2, 3,4,5,6, 7,8,9. Римськими І, V, X, L, С, D, М 1 5 10 50 100 500 1000 в азбуці Морзе в шрифті Брайля

Пригадаємо “Синтез думок” ? ? Cформулюйте означення N, Z, Q.

N Q Z 0, -1, -2, -3, … “+” і “-” дро - бові Сформулюйте означення R

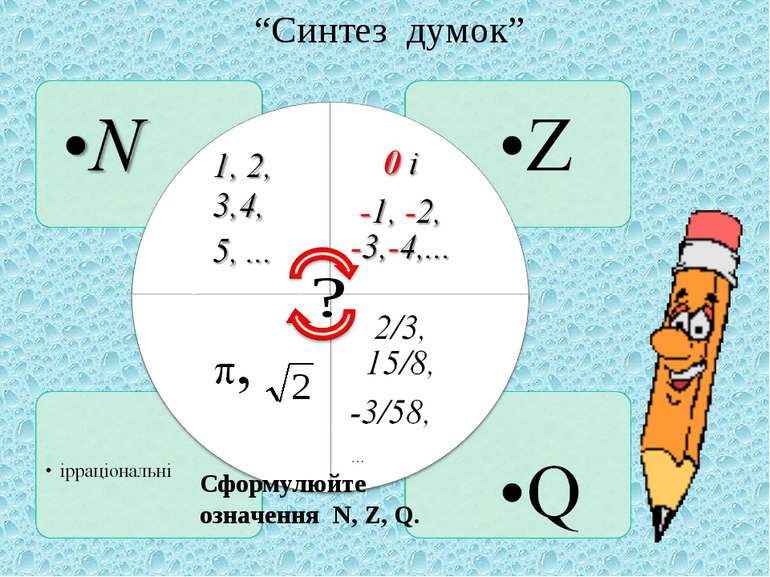
Уявлення про дійсні числа Дійсні числа – числова система, яка містить в собі раціональні числа і, в свою чергу, міститься у комплексних числах. Дійсні числа можна додавати, віднімати, множити і ділити (окрім ділення на нуль), і для них спроваджуються всі правила арифметики (комутативність, асоціативність, дистрибутивність, і т.д.). Але на відміну від раціональних чисел, вони також замкнені відносно операції граничного переходу. Тому дійсні числа належать до підвалин математичного аналізу.

Історична довідка Означення дійсних чисел дані Ріхардом Дедекіндом через перерізи

Георгом Кантором через послідовності Карлом Вейєрштрассом через нескінченні десяткові дроби

Над відмінностями множини R від множини Q працювали: Огюстен Коші Едуард Гейне

Конструктивні способи побудови дійсних чисел Переріз Дедекінда — це конструкція з математичного аналізу запропонована Ріхардом Дедекіндом, за допомогою якої надається математично строге визначення дійсних чисел.

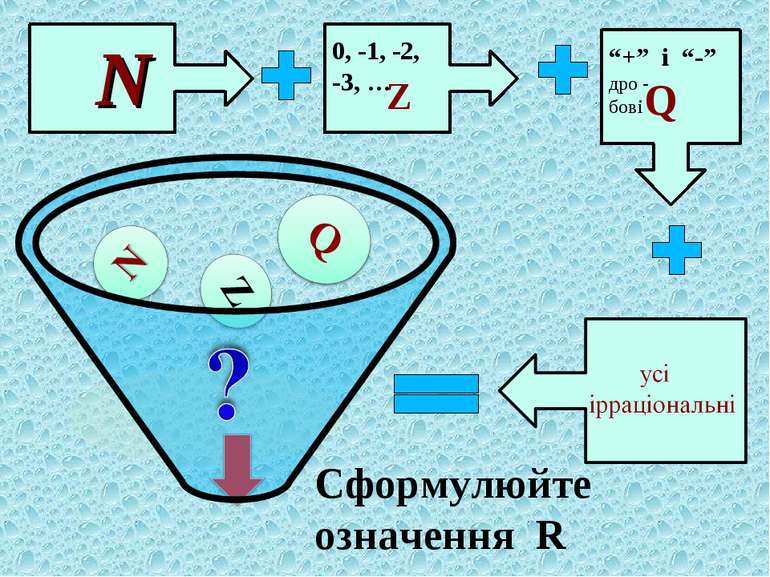
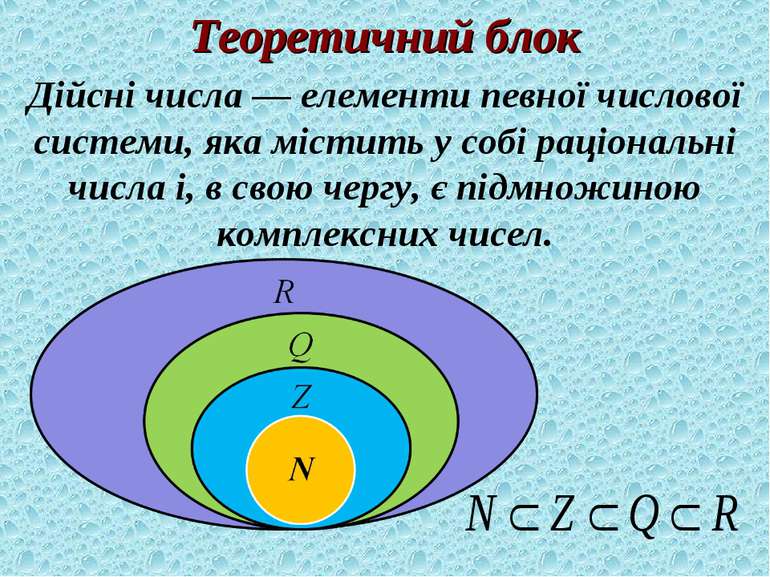
Теоретичний блок Дійсні числа — елементи певної числової системи, яка містить у собі раціональні числа і, в свою чергу, є підмножиною комплексних чисел.

Теоретичний блок Зверніть увагу: кожне натуральне число є цілим, кожне ціле — раціональним, кожне раціональне — дійсним. Приклади ірраціональних чисел: ...; 0,12345...; 10,1010010001...; ... Дійсні числа можна додавати, віднімати, множити, підносити до степеня й ділити (ділити — на числа, що відмінні від 0). Усі відомі властивості дій залишаються такими ж.

Теоретичний блок Кожному дійсному числу відповідає єдина точка координатної прямої. яку називають числовою прямою.

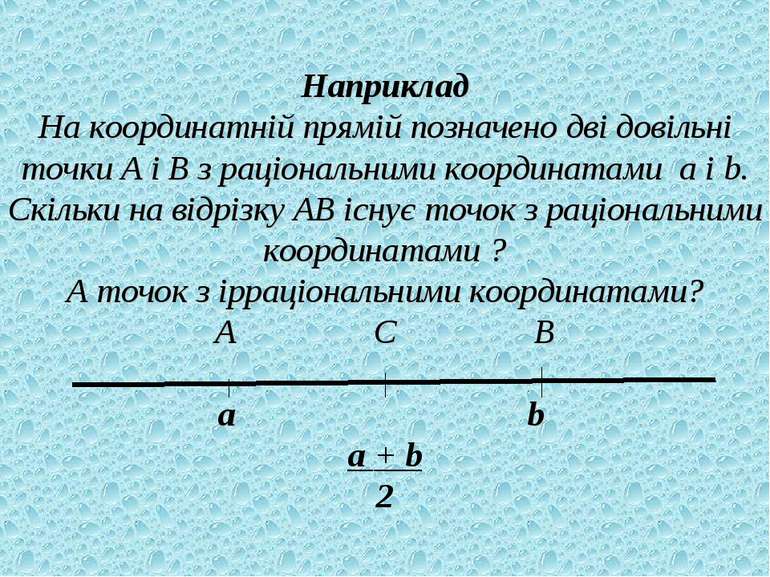
Наприклад На координатній прямій позначено дві довільні точки А і В з раціональними координатами a і b. Скільки на відрізку АВ існує точок з раціональними координатами ? А точок з ірраціональними координатами? А С В а b а + b 2

Теоретичний блок Дійсні числа - елементи множини R, на якій визначені операції “ +” і “ ∙ ”, елементи 0 і 1, відношення порядку “ >”, що задовольняють установлену систему властивостей.

Для додавання і множення дійсних чисел a, b, c справджються такі закони: а + b= b + a; а + (b + c)=(a + b) + c; а(bc) = (ab)c; аb = ba; (a + b)c = ac + bc

Властивості “ + ” ,“∙” раціональних чисел

Порівняння дійсних чисел ?

Порівняння дійсних чисел ?

Порівняння дійсних чисел ?

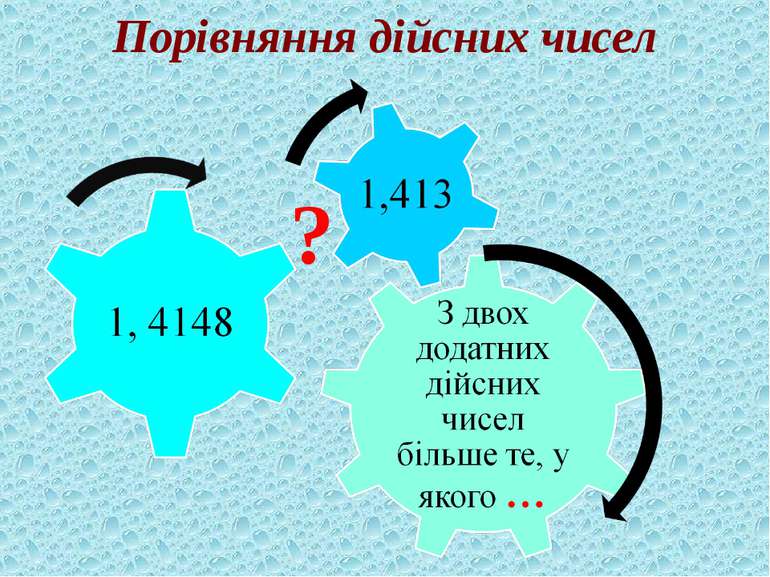
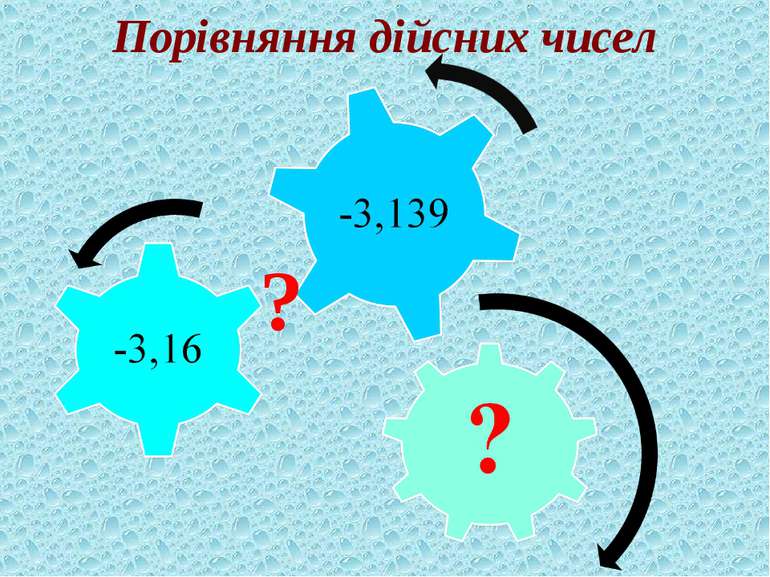
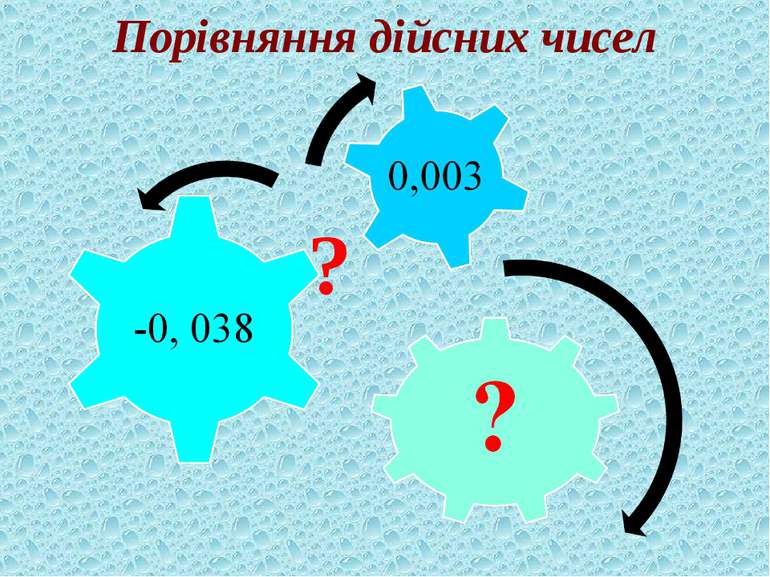
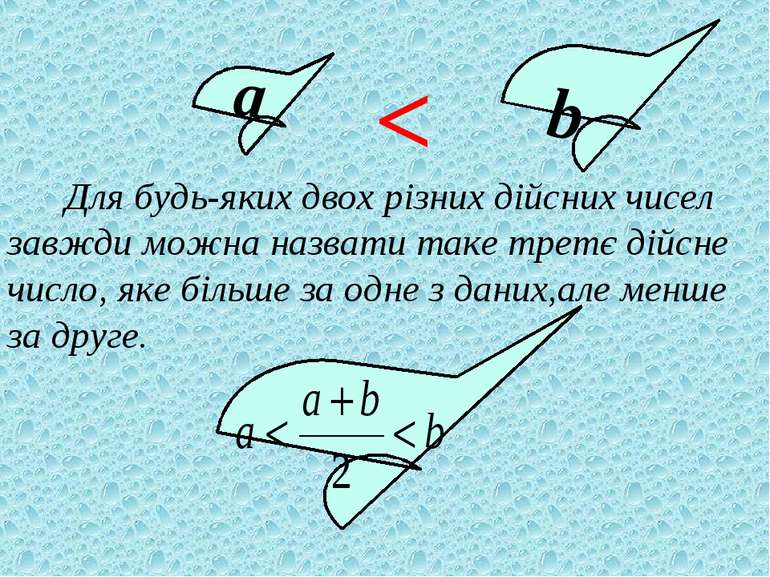
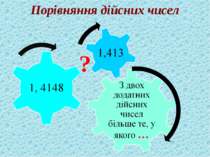
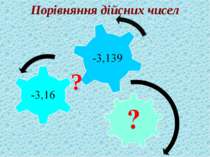
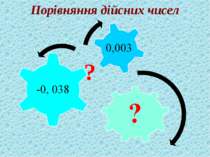
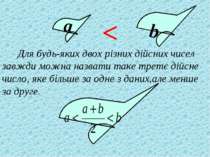
Для будь-яких двох різних дійсних чисел завжди можна назвати таке третє дійсне число, яке більше за одне з даних,але менше за друге. b а <

Яке з тверджень правильне: а) кожне натуральне число є дійсним; б) кожне ціле число є дійсним; в) кожне раціональне число є дійсним; г) кожне ірраціональне число є дійсним; ґ) не кожне дійсне число є раціональним; д) не кожне дійсне число є ірраціональним? Тест ”Інтелектуальна розминка”

Завдання 1 Розгляньте рівності. Чи правильні вони? Які закономірності ви помітили? Спробуйте продовжити записи. а) 1 + 9⋅0 = 1, б) 1 + 8⋅1 = 9, 2 + 9⋅1 = 11, 2 + 8⋅12 = 98, 3 + 9⋅12 = 111; 3 + 8⋅123 = 987.

Завдання 2 Уявіть, що якась жінка М на початку нашої ери народила двох дочок, кожна з яких до 33 років народила також не менше двох дочок, а кожна з них – також не менше двох дочок і т. д. Скільки нащадків жінки М жило б за таких умов у наші дні? Чи могло б таке бути?

Дякую за увагу. Бажаю математичних звершень !