Презентація на тему:
Застосування інтегралів до знаходження площ та об'ємів

Обобщить и систематизировать знания по теме «Первообразная»; Проведение тестирования с целью проверки знаний учащихся ; Изучить формулы нахождения площадей различных фигур; Отработка навыка нахождения площадей фигур, ограниченных графиками различных функций.

2х Найти производную функции: sin 2x 2 3 ln x 2 cos 2x

Найти первообразную функции: ln x sin 2x

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ИНТЕГРАЛА

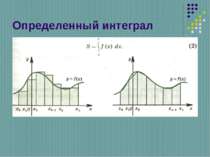
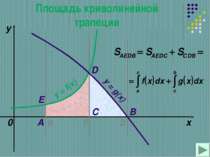
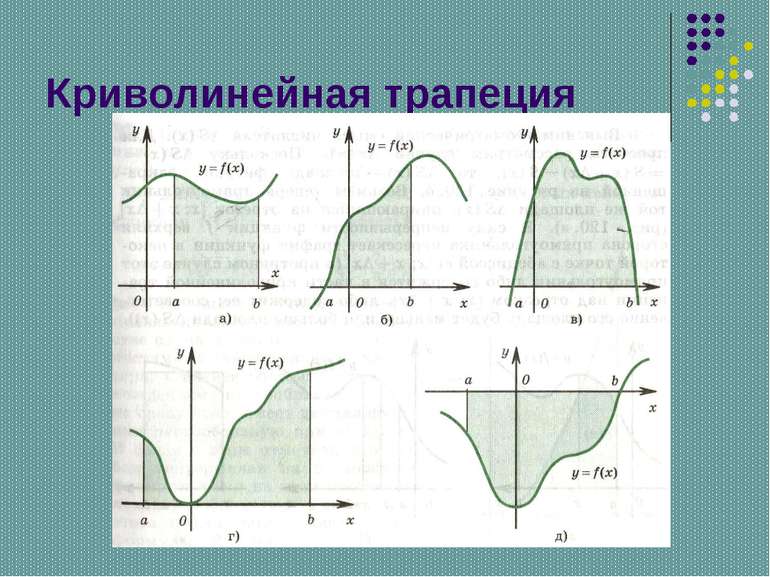
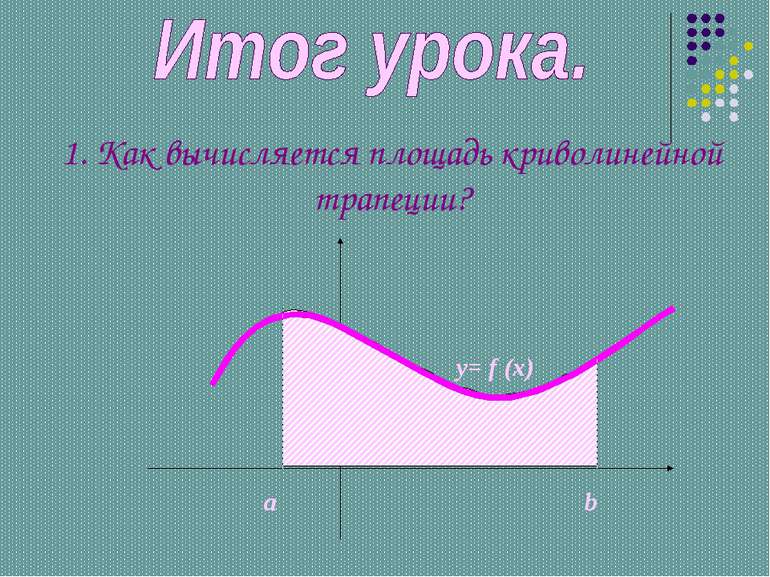
Определение Криволинейной трапецией называется фигура, ограниченная графиком неотрицательной и непрерывной на отрезке [a;b]  функции  f, осью Ox и прямыми  x = a и x =  b.

Криволинейная трапеция

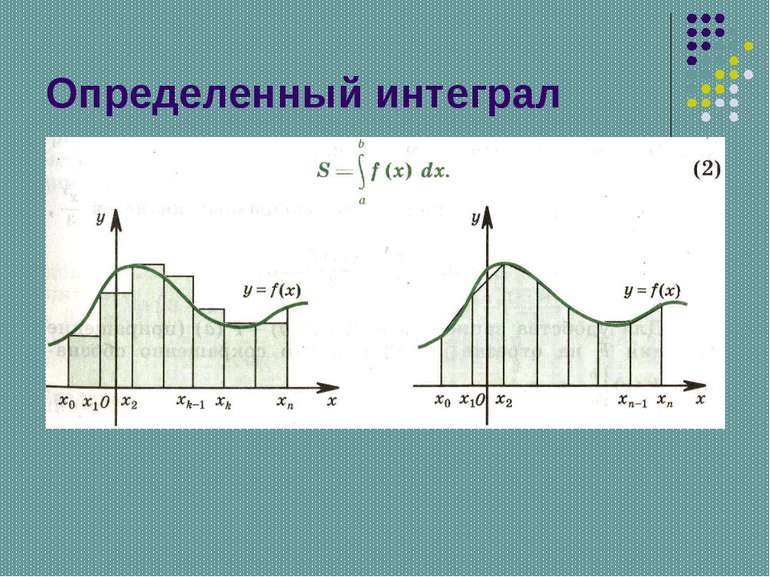
у х Рассматривая непрерывную функцию у=f(х), неотрицательную на отрезке [а;в], отрезок [а;в] разбиваем на n равных частей точками а=х0

Числа a и в называют пределами интегрирования: а- нижний предел, в – верхний предел, функцию у=f(х) – подынтегральной функцией, выражение f(х)dх – подынтегральным выражением, переменную х – переменной интегрирования. Таким образом

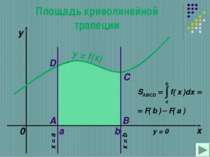
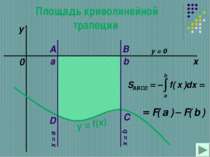
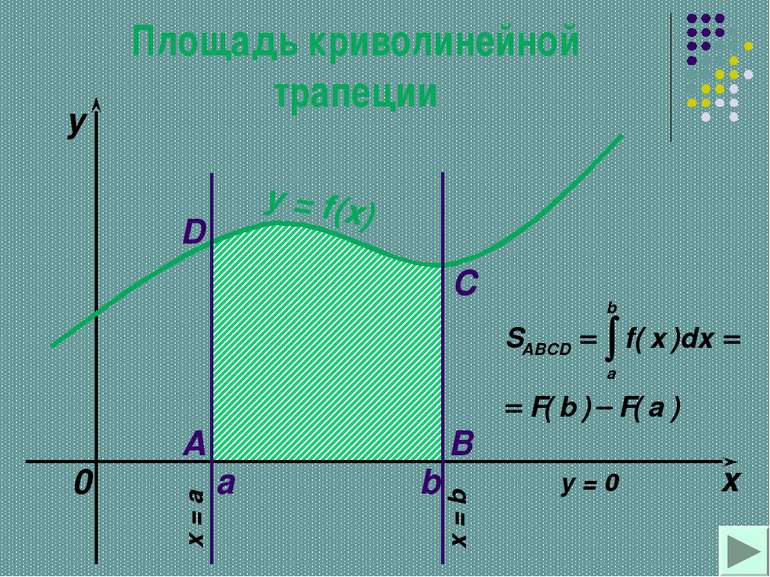
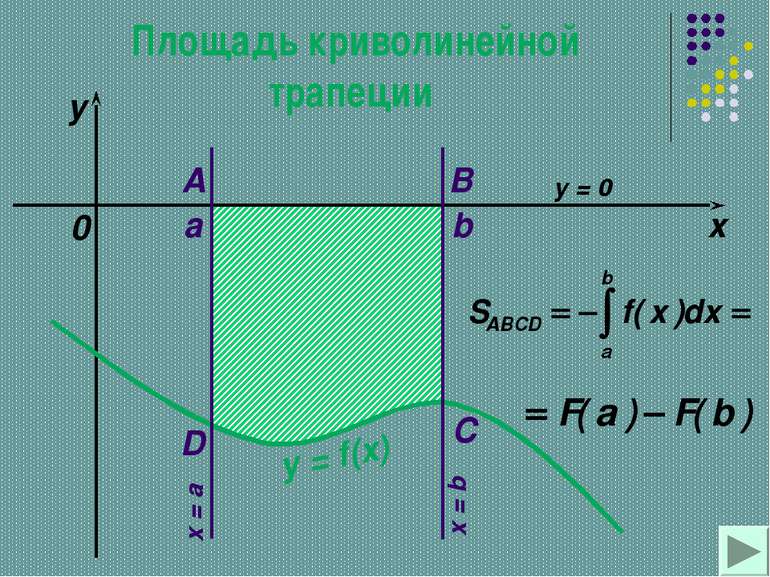
Теорема Если f-непрерывная и неотрицательная на [a,b] функция, а F –ее первообразная на этом отрезке, то площадь S соответствующей криволинейной трапеции равна приращению первообразной на отрезке [a,b], т.е. S=F(b)-F(a)

Определенный интеграл

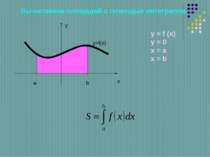
Определенный интеграл – формула Ньютона-Лейбница. Геометрический смысл определенного интеграла заключается в том, что определенный интеграл равен площади криволинейной трапеции, образованной линиями: сверху ограниченной кривой у = f(x),  и прямыми у = 0; х = а; х = b.

Вычисление определенного интеграла

Площадь криволинейной трапеции a b x y y = f(x) 0 A B C D x = a x = b y = 0

РЕШАЕМ ВМЕСТЕ Вычислить площадь треуголь-ника, ограниченного осью ОХ, прямыми х=к и у=2х. РЕШЕНИЕ Здесь криволинейная трапеция имеет вид прямоугольного треугольника, причем а=0, в=к, а функция у=2х, график которой ограничивает треугольник, положительна и непрерывна на [0;к]. Найдем определенный интеграл к 0 у х У=2х

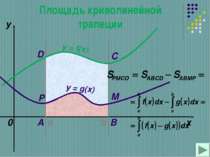
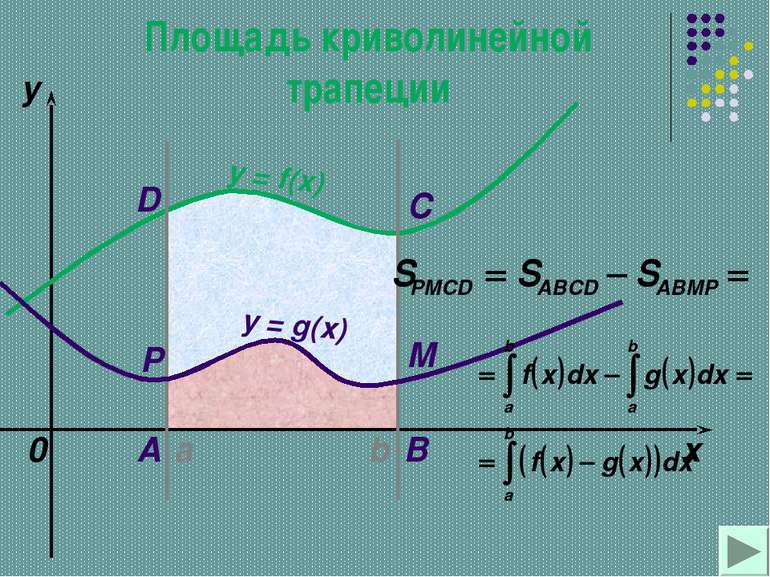
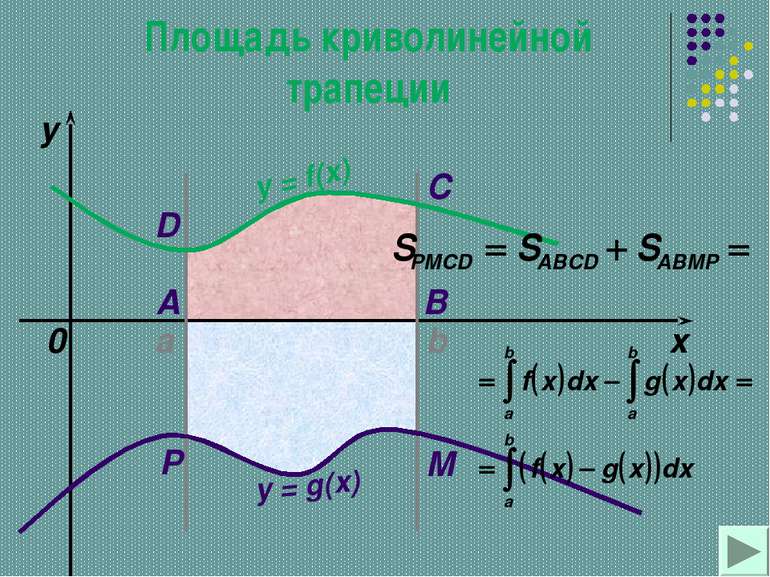
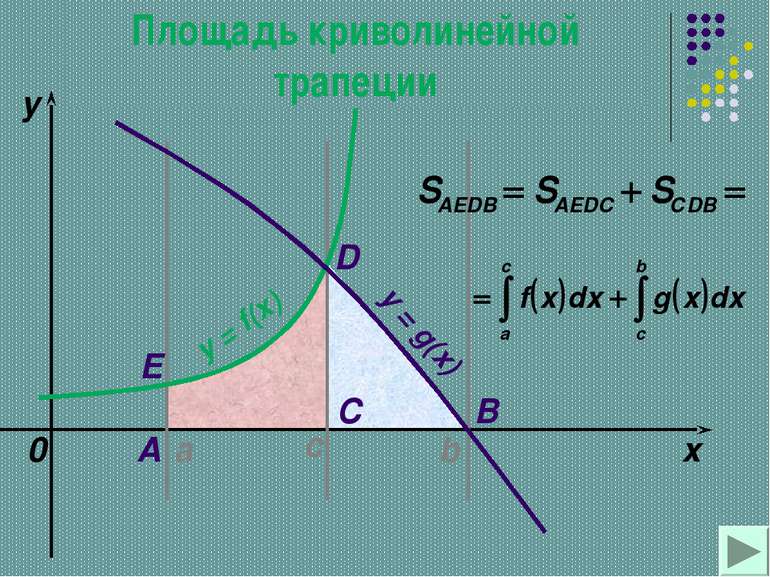
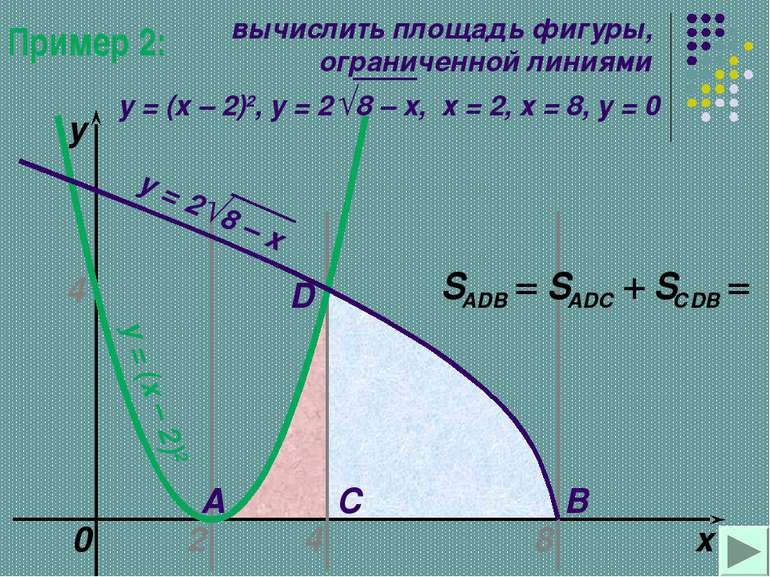
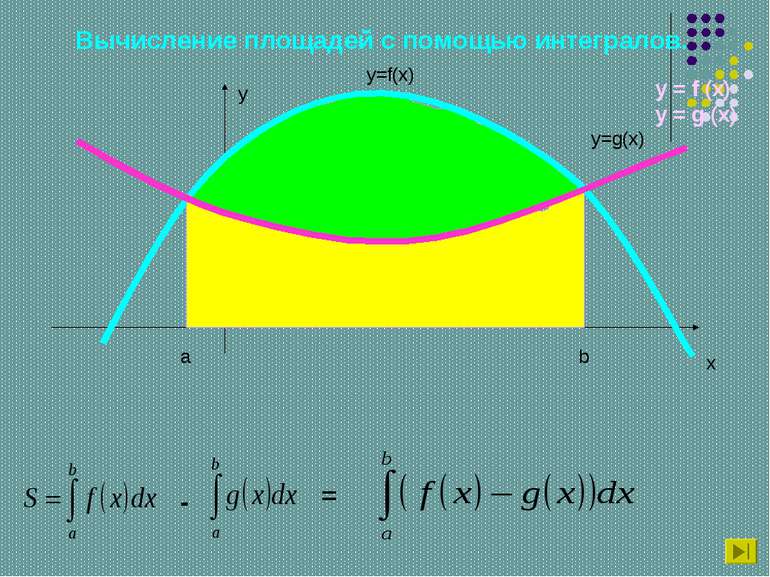
НАХОЖДЕНИЕ ПЛОЩАДЕЙ КРИВОЛИНЕЙНЫХ ТРАПЕЦИЙ,ОГРАНИЧЕННЫХ ГРАФИКАМИ ДВУХ НЕПРЕРЫВНЫХ ФУНКЦИЙ Существует много вариантов, и сейчас мы с вами некоторые из них рассмотрим.

Площадь криволинейной трапеции a b x y y = f(x) 0 A B C D x = a x = b y = 0

a b x y y = f(x) 0 y = g(x) A B C D M P Площадь криволинейной трапеции

a b x y y = f(x) 0 y = g(x) A B C D M P Площадь криволинейной трапеции

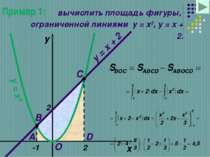
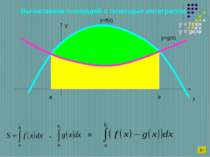
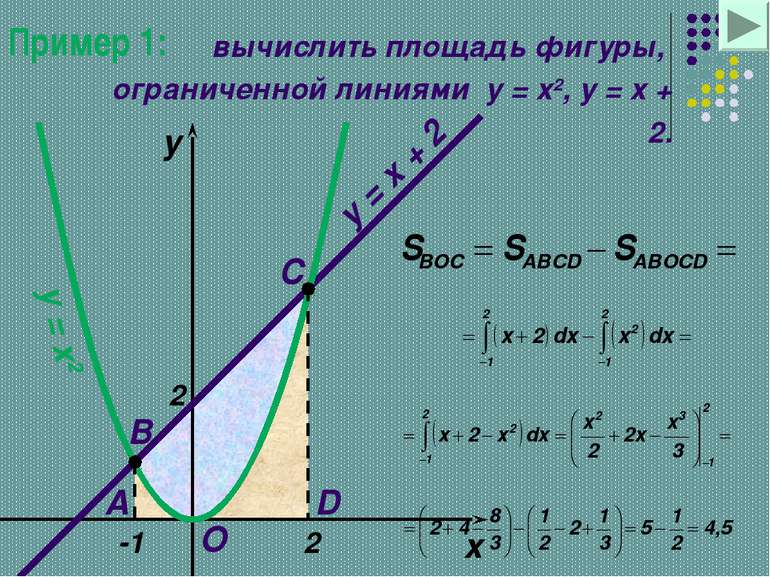
Пример 1: вычислить площадь фигуры, ограниченной линиями y = x2, y = x + 2. x y y = x2 y = x + 2 -1 2 A B O D C 2

a b x y y = f(x) 0 y = g(x) A B C D с Е Площадь криволинейной трапеции

Пример 2: 2 8 x y = (x – 2)2 0 A B C D 4 y 4

Пример 2:

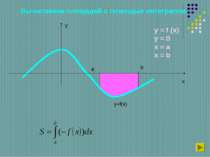
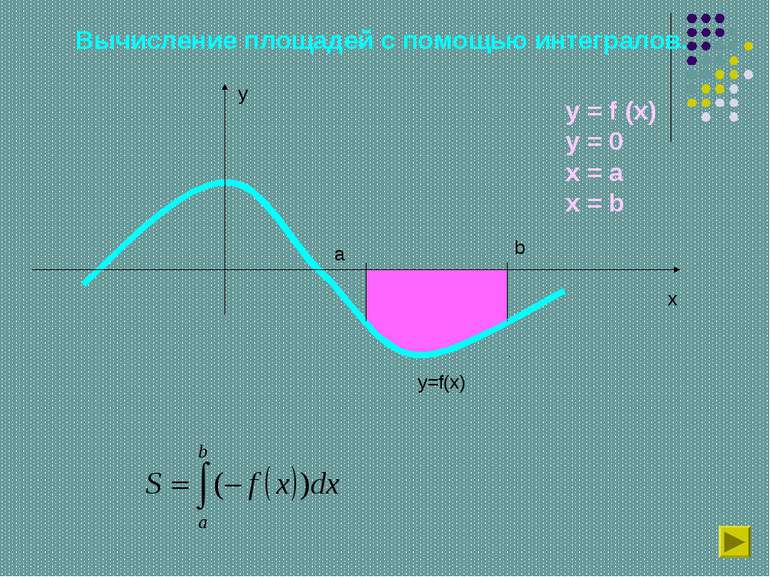
РЕШИМ ЕЩЕ ОДНУ ЗАДАЧУ Вычислить площадь фигуры, ограниченной синусоидой у=sinх и отрезком [0;π] оси Ох. РЕШЕНИЕ ОТВЕТ: площадь фигуры 1 кв. ед. у х 0

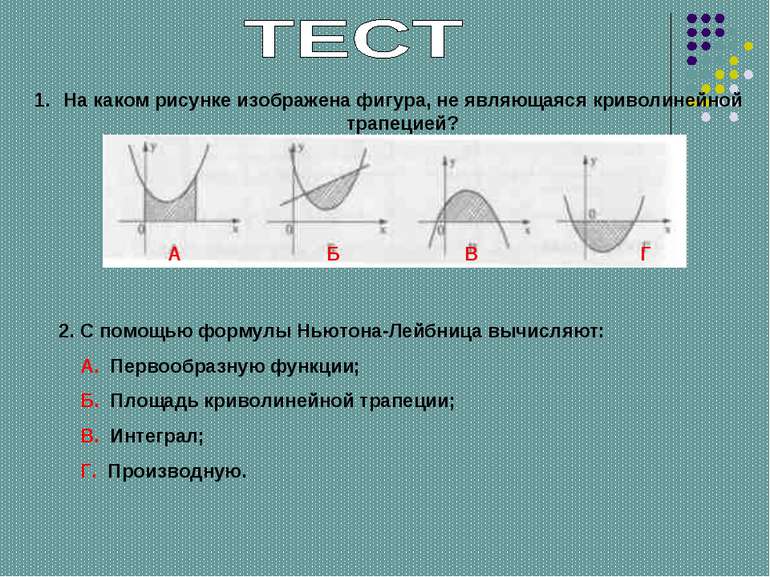
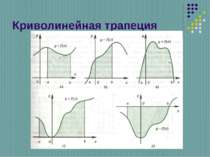
На каком рисунке изображена фигура, не являющаяся криволинейной трапецией? 2. С помощью формулы Ньютона-Лейбница вычисляют: А. Первообразную функции; Б. Площадь криволинейной трапеции; В. Интеграл; Г. Производную. А Б В Г

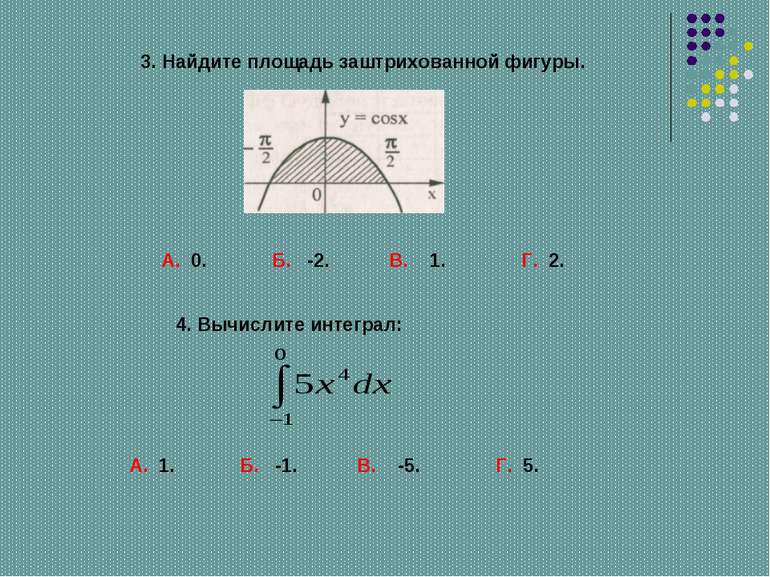
3. Найдите площадь заштрихованной фигуры. А. 1. Б. -1. В. -5. Г. 5. 4. Вычислите интеграл: А. 0. Б. -2. В. 1. Г. 2.

А. 2a. Б. 2cos a. В. 0. Г. 2. 5. Вычислите интеграл: А. . Б. . В. . Г. .

Вычисление площадей с помощью интегралов. a b y x y=f(x) y = f (x) y = 0 x = a x = b

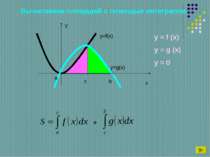
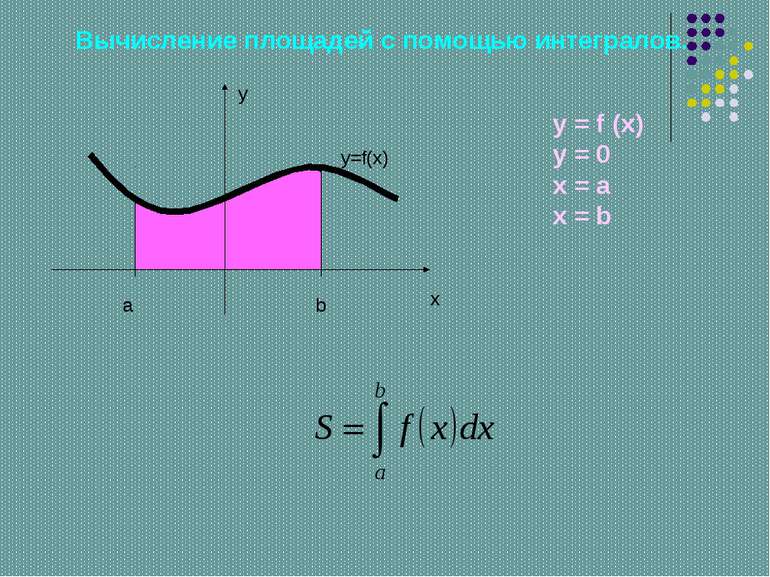
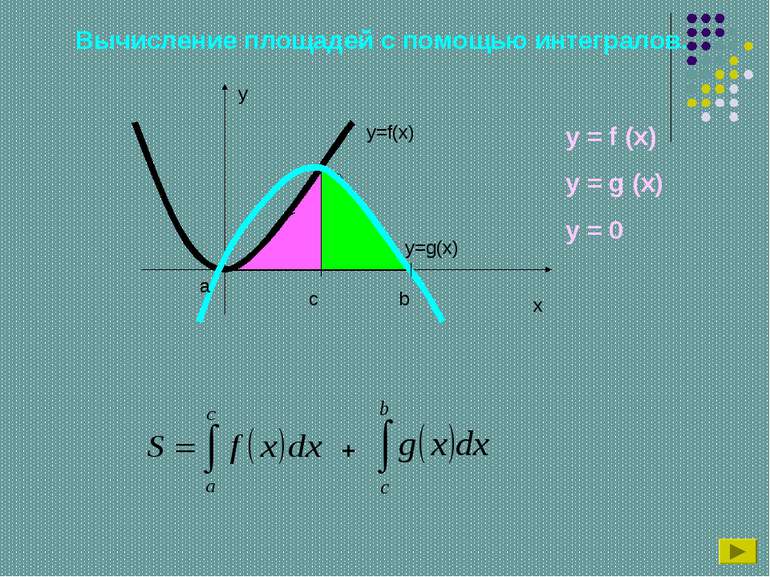
Вычисление площадей с помощью интегралов. y x y=f(x) a b c y=g(x) + y = f (x) y = g (x) y = 0

Вычисление площадей с помощью интегралов. y x y=f(x) a b y = f (x) y = 0 x = a x = b

Вычисление площадей с помощью интегралов. y x y=f(x) a b y=g(x) - = y = f (x) y = g (x)

Вычисление объемов тел с помощью определенного интеграла

Объем Объемом тела называется положительная величина, характеризующая часть пространства, занимаемую телом, и обладающая следующими свойствами: -равные тела имеют равные объемы; -при параллельном переносе тела его объем не изменяется; -если тело разбить на части, являющиеся простыми телами, то объем тела равен объему его частей; -за единицу объема принят объем куба, ребро которого равно единице длины;

Объем тела вращения Пусть тело образуется при вращении вокруг оси OX криволинейной трапеции x1ABx2 Любое сечение этого тела плоскостью, перпендикулярной к оси Ox будет круг, радиус которого равен соответствующей ординате точки кривой Y=f(x) Площадь сечения S(x) равна y2, т.е. S(x)= f2(x) Объем тела вращения может быть вычислен по формуле

ЗАДАЧА Вычислить объем шара, получаемого вращением полуокружности вокруг оси OX Построим полуокружность y X R -R R При вращении этой полуокружности вокруг OX получается сфера, ограничивающая шар. Объем шара найдем по формуле Ответ: Объем шара (куб.ед.)

ВЫЧИСЛИТЬ ИНТЕГРАЛЫ

Вычислить площади плоских фигур, ограниченных линиями: у=х², у=4 у=х³, осью Ох и прямой х=2 параболой у=1-х² и осью Ох параболой у=х² и прямой у=х+1 графиком функции у= -х²+4 и прямой х+у=4 графиками функций у= -х²+2х+8, у=х²+2х+2 параболой у=х²+1 и прямой 5х+3у-25=0 линиями у=0, у= -х²+3, х=1, х=1,5 кривой у=х³ и прямыми у=1, х=-2 прямой у=х и параболой у=2-х² линиями у=(х+1)² и у=4-х параболой у=х²+2х-8 и осью Ох.

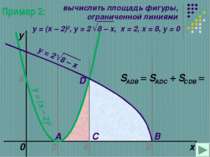
НАЙТИ ОБЪЕМЫ ТЕЛ Образованного вращением вокруг оси Оу фигуры, ограниченной прямыми у=2х, х=0,у=5; Образованного вращением вокруг оси Ох фигуры, ограниченной синусоидой и прямыми х=0 и х=π/2; Образованного вращением вокруг оси Ох фигуры, ограниченной кривой у=х³ и прямыми х=1 и х=2; Образованного вращением усеченного конуса с радиусами оснований r1 и r2 и высотой Н.

1. Как вычисляется площадь криволинейной трапеции? a b y= f (x)

2. Как вычисляется площадь фигуры ограниченной графиками различных функций?

3. Как вычисляется объём тела вращения криволинейной трапеции вокруг оси ОХ?