Презентація на тему:
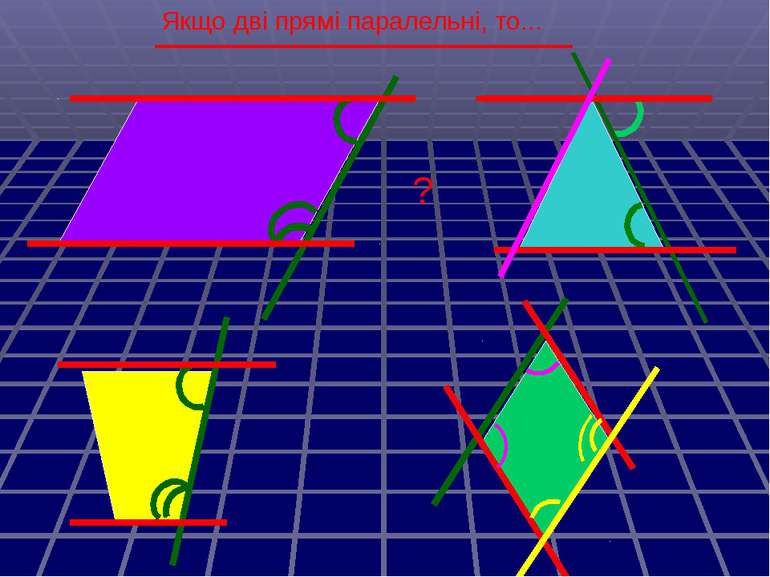
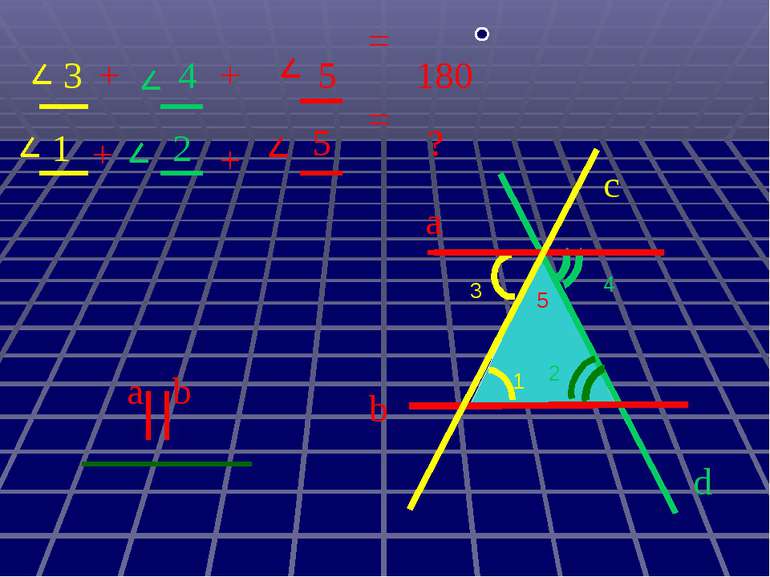
Властивості кутів, утворених при перетині паралельних прямих січною

Пролунав уже дзвінок! Починаємо урок!

Все в природі повинно бути виміряно, все може бути пораховано. Лобачевський М.І.

ІСТОРИЧНА ЗУПИНКА ЗУПИНКА ДОВЕДЕНЬ ЗУПИНКА ЗАКРІПЛЕННЯ знань ПІДГОТОВЧА ЗУПИНКА ПІДСУМКОВА ЗУПИНКА ДОСЛІДНИЦЬКА ЗУПИНКА

ПІДГОТОВЧА ЗУПИНКА Повторити розташування і назви кутів… Згадати ознаки паралельності прямих. Сформулювати мету і тему уроку

1 2 3 4 5 6 7 8 9 10 11

Д З В О Н И К 2 3 4 5 6 7 8 9 10 11

Д З В О Н И К П А Р А Л Е Л Ь Н І 3 4 5 6 7 8 9 10 11

Д З В О Н И К П А Р А Л Е Л Ь Н І О З Н А К И 4 5 6 7 8 9 10 11

Д З В О Н И К П А Р А Л Е Л Ь Н І О З Н А К И 4 5 6 7 8 9 10 11

Д З В О Н И К П А Р А Л Е Л Ь Н І О З Н А К И С І Ч Н А 5 6 7 8 9 10 11

Д З В О Н И К П А Р А Л Е Л Ь Н І О З Н А К И С І Ч Н А Р І З Н О С Т О Р О Н Н І 6 7 8 9 10 11

b 2 c a 6 5 4 3 1 8 7

Д З В О Н И К П А Р А Л Е Л Ь Н І О З Н А К И С І Ч Н А Р І З Н О С Т О Р О Н Н І 6 7 8 9 10 11

Д З В О Н И К П А Р А Л Е Л Ь Н І О З Н А К И С І Ч Н А Р І З Н О С Т О Р О Н Н І В Е Р Т И К А Л Ь Н І 7 8 9 10 11

b 2 c a 6 5 4 3 1 8 7

Д З В О Н И К П А Р А Л Е Л Ь Н І О З Н А К И С І Ч Н А Р І З Н О С Т О Р О Н Н І В Е Р Т И К А Л Ь Н І 7 8 9 10 11

Д З В О Н И К П А Р А Л Е Л Ь Н І О З Н А К И С І Ч Н А Р І З Н О С Т О Р О Н Н І В Е Р Т И К А Л Ь Н І В Н У Т Р І Ш Н І 8 9 10 11

b 2 c a 6 5 4 3 1 8 7

Д З В О Н И К П А Р А Л Е Л Ь Н І О З Н А К И С І Ч Н А Р І З Н О С Т О Р О Н Н І В Е Р Т И К А Л Ь Н І В Н У Т Р І Ш Н І 8 9 10 11

Д З В О Н И К П А Р А Л Е Л Ь Н І О З Н А К И С І Ч Н А Р І З Н О С Т О Р О Н Н І В Е Р Т И К А Л Ь Н І В Н У Т Р І Ш Н І З О В Н І Ш Н І 9 10 11

b 2 c a 6 5 4 3 1 8 7

Д З В О Н И К П А Р А Л Е Л Ь Н І О З Н А К И С І Ч Н А Р І З Н О С Т О Р О Н Н І В Е Р Т И К А Л Ь Н І В Н У Т Р І Ш Н І З О В Н І Ш Н І 9 10 11

Д З В О Н И К П А Р А Л Е Л Ь Н І О З Н А К И С І Ч Н А Р І З Н О С Т О Р О Н Н І В Е Р Т И К а Л Ь Н І В Н У Т Р І Ш Н І З О В Н І Ш Н І О Д Н О С Т О Р О Н Н І 10 11

b 2 c a 6 5 4 3 1 8 7

Д З В О Н И К П А Р А Л Е Л Ь Н І О З Н А К И С І Ч Н А Р І З Н О С Т О Р О Н Н І В Е Р Т И К а Л Ь Н І В Н У Т Р І Ш Н І З О В Н І Ш Н І О Д Н О С Т О Р О Н Н І 10 11

Д З В О Н И К П А Р А Л Е Л Ь Н І О З Н А К И С І Ч Н А Р І З Н О С Т О Р О Н Н І В Е Р Т И К а Л Ь Н І В Н У Т Р І Ш Н І З О В Н І Ш Н І О Д Н О С Т О Р О Н Н І Т Р А Н С П О Р Т И Р 11

Д З В О Н И К П А Р А Л Е Л Ь Н І О З Н А К И С І Ч Н А Р І З Н О С Т О Р О Н Н І В Е Р Т И К А Л Ь Н І В Н У Т Р І Ш Н І З О В Н І Ш Н І О Д Н О С Т О Р О Н Н І Т Р А Н С П О Р Т И Р Г Е О М Е Т Р І Я

Д З В О Н И К П А Р А Л Е Л Ь Н І О З Н А К И С І Ч Н А Р І З Н О С Т О Р О Н Н І В Е Р Т И К А Л Ь Н І В Н У Т Р І Ш Н І З О В Н І Ш Н І О Д Н О С Т О Р О Н Н І Т Р А Н С П О Р Т И Р Г Е О М Е Т Р І Я

Якщо дві прямі паралельні, то... ?

Властивості кутів, утворених при перетині паралельних прямих січною.

ДОСЛІДНИЦЬКА ЗУПИНКА Провести практичний, контролюючий і теоретичний досліди .

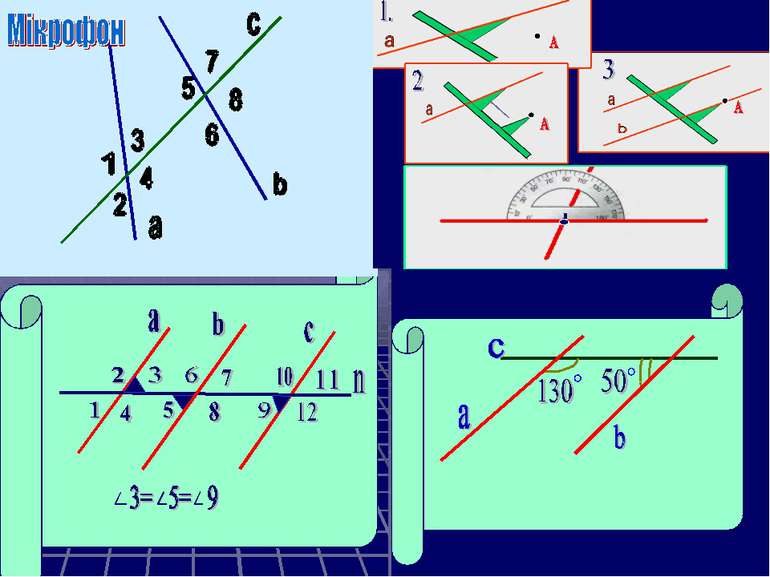
1.Проведіть довільну пряму b. 2. Поставте точку А, яка б не належала прямій. 3. За допомогою косинця та лінійки побудуйте пряму а , паралельну b, і яка б проходила через А . 4. Проведіть січну . 5. Позначте: - внутрішні різносторонні кути цифрами -1 і 2 ; - внутрішні односторонні -1 і 3, - відповідні – 4 і 3 5. Виміряйте їх величину за допомогою транспортира. 6. Запишіть результати вимірів у зошит. 7. Зробіть висновок для кожного випадку, порівнявши величини кутів. Дослід перший - практичний.

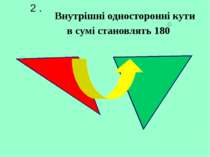
ВИСНОВОК. Якщо дві паралельні прямі перетинаються січною, то: - внутрішні різносторонні кути … … … ; - внутрішні односторонні кути в сумі становлять … … ; - відповідні кути … ... … ; р і в н і

ВИСНОВОК. Якщо дві паралельні прямі перетинаються січною, то: - внутрішні різносторонні кути … … … ; - внутрішні односторонні кути в сумі становлять … … ; - відповідні кути … ... … ; р і в н і р і в н і 180º

ВИСНОВОК. Якщо дві паралельні прямі перетинаються січною, то: - внутрішні різносторонні кути … … … ; - внутрішні односторонні кути в сумі становлять … … ; - відповідні кути … ... … . р і в н і р і в н і 180º

Дослід другий - контролюючий.

1. Внутрішні різносторонні кути рівні.

2 . Внутрішні односторонні кути в сумі становлять 180

3. Відповідні кути рівні.

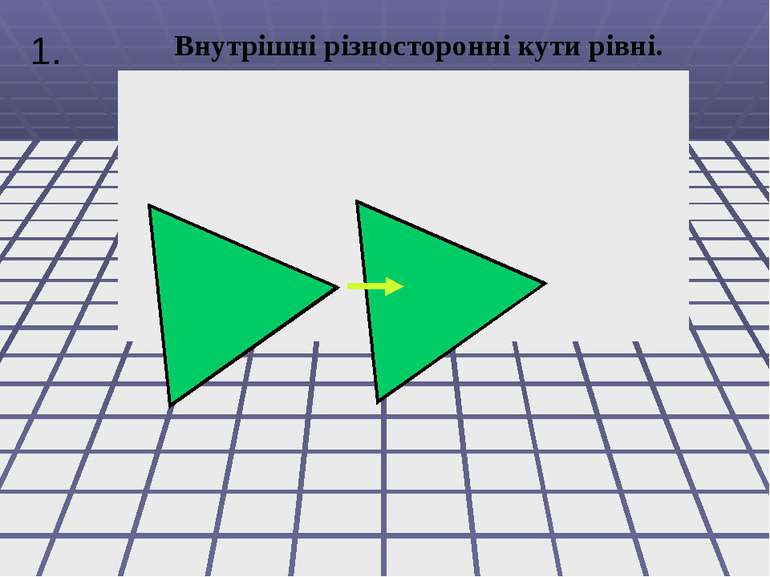
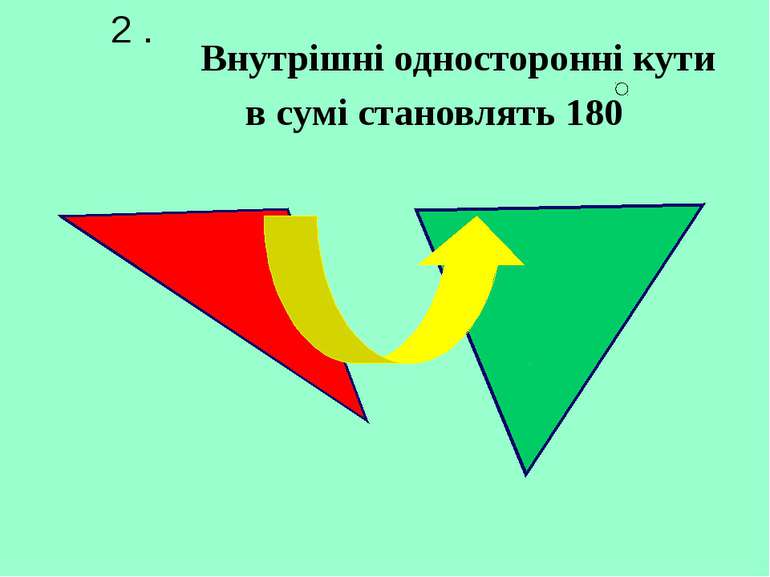
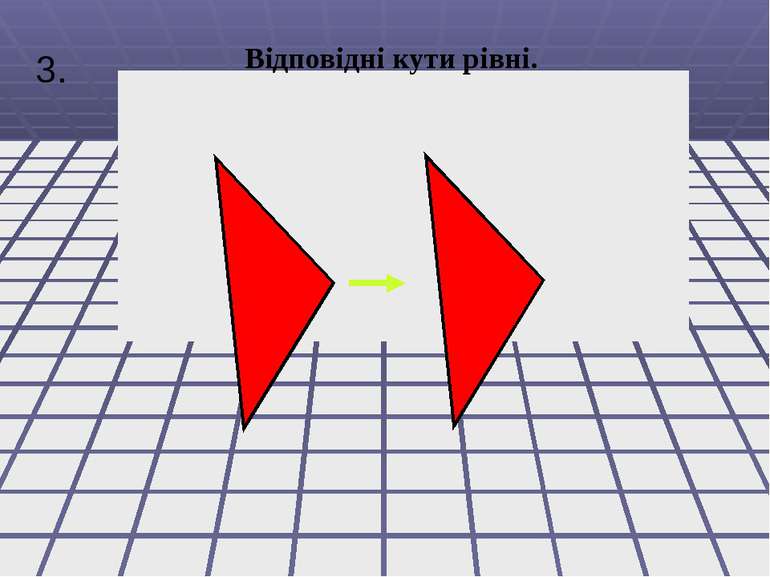
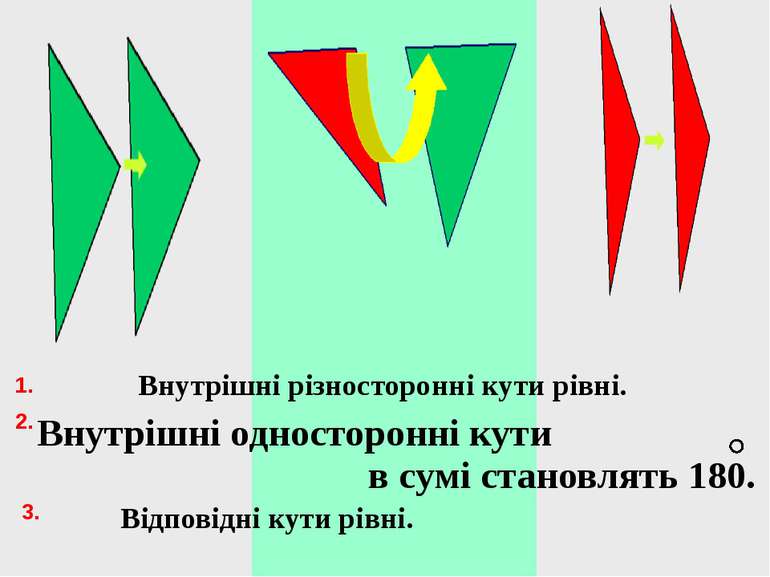
Внутрішні різносторонні кути рівні. Внутрішні односторонні кути в сумі становлять 180. Відповідні кути рівні. 1. 2. 3.

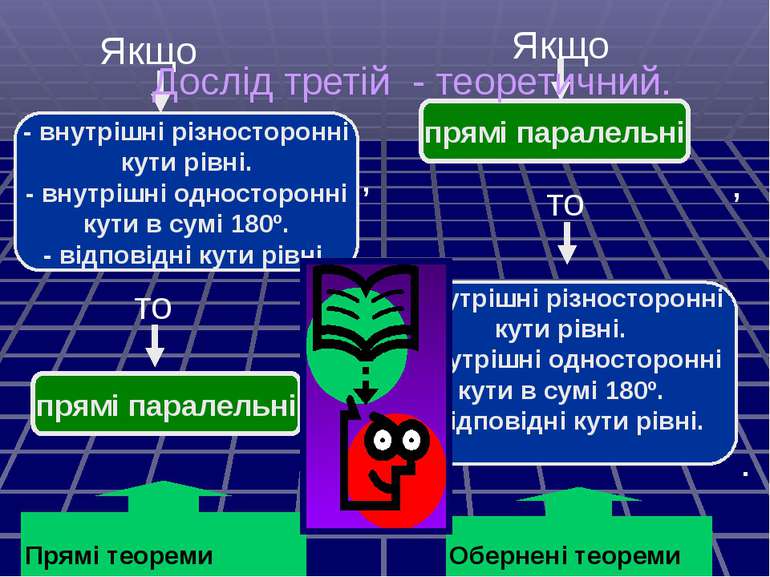
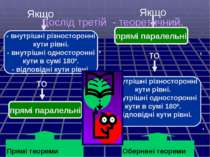
- внутрішні різносторонні кути рівні. - внутрішні односторонні кути в сумі 180º. - відповідні кути рівні. прямі паралельні Якщо , то . Якщо прямі паралельні то - внутрішні різносторонні кути рівні. - внутрішні односторонні кути в сумі 180º. - відповідні кути рівні. , . Прямі теореми Обернені теореми Дослід третій - теоретичний.

Якщо прямі паралельні, то … 1). Якщо при перетині із січною утворюються рівні внутрішні різносторонні кути, то прямі паралельні. 2). Якщо при перетині із січною утворюються внутрішні односторонні кути, сума яких 180º , 3). Якщо при перетині із січною утворюються рівні відповідні кути, то прямі паралельні. то прямі паралельні.

ІСТОРИЧНА ЗУПИНКА ДОСЛІДНИЦЬКА ЗУПИНКА Відшукати властивості кутів теоретичним і практичним шляхом.

Евклід- грецький математик ( ст.до н.е.)

Аксіома Евкліда. Через точку, яка не лежить на даній прямій, можна провести тільки одну пряму, паралельну даній. а b А

ЗУПИНКА ДОВЕДЕНЬ Довести одну з властивостей кутів... Ознайомитися з методом доведення від супротивного.

Маленька зупинка - фізкультхвилинка !

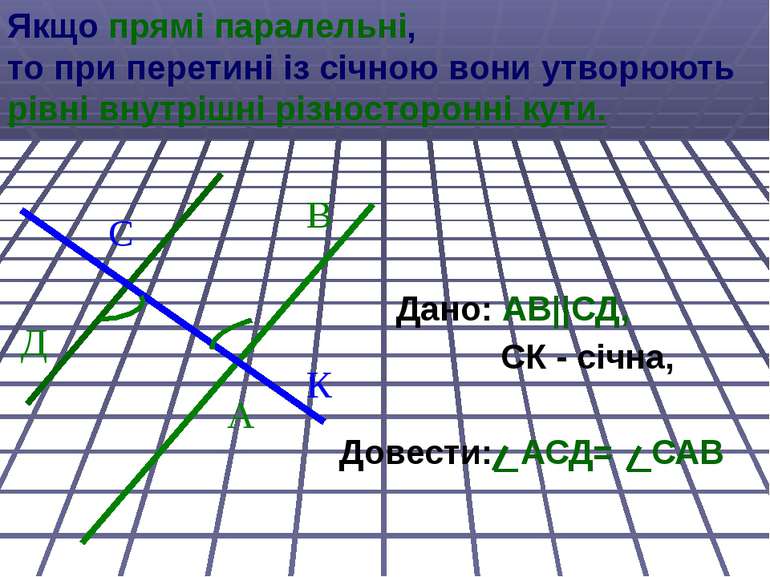
Якщо прямі паралельні, то при перетині із січною вони утворюють рівні внутрішні різносторонні кути. Дано: АВ||СД, СК - січна, Довести: АСД= САВ А С Д К В

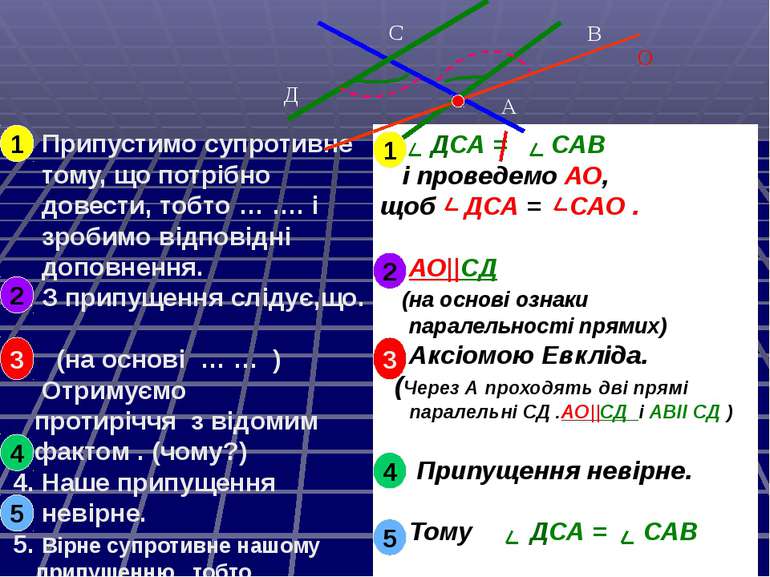
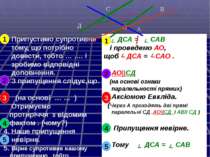
Дано: АВ ||СД, СК- січна, Довести: САВ = АСД. Доведення. Припустимо, що АВ||СД, а САВ = АСД. Проведемо АО щоб, САО = АСД . За припущенням (на основі ознаки паралельності прямих) АО||СД. За умовою АВ||СД. Через А проходять дві прямі паралельні СД, що суперечить аксіомі Евкліда. Припущення невірне. Тому САВ = АСД В А Д С О К

Припустимо супротивне тому, що потрібно довести, тобто … …. і зробимо відповідні доповнення. 2. З припущення слідує,що. (на основі … … ) Отримуємо протиріччя з відомим фактом . (чому?) 4. Наше припущення невірне. 5. Вірне супротивне нашому припущенню , тобто … . ДСА = САВ і проведемо АО, щоб ДСА = САО . 2. АО||СД (на основі ознаки паралельності прямих) 3. Аксіомою Евкліда. (Через А проходять дві прямі паралельні СД .АО||СД і АВІІ СД ) 4. Припущення невірне. 5. Тому ДСА = САВ В А Д С О 1 1 2 2 3 3 4 4 5 5

§ 7, №200.

1. Припустимо супротивне тому, що потрібно довести, тобто . . . . . . . . . . . . . . . . . . . . . . 2. З припущення слідує, що. . . . (на основі … ... … … ) 3. Отримуємо протиріччя з ….. 4. Наше припущення невірне. Вірне супротивне йому, тобто ………

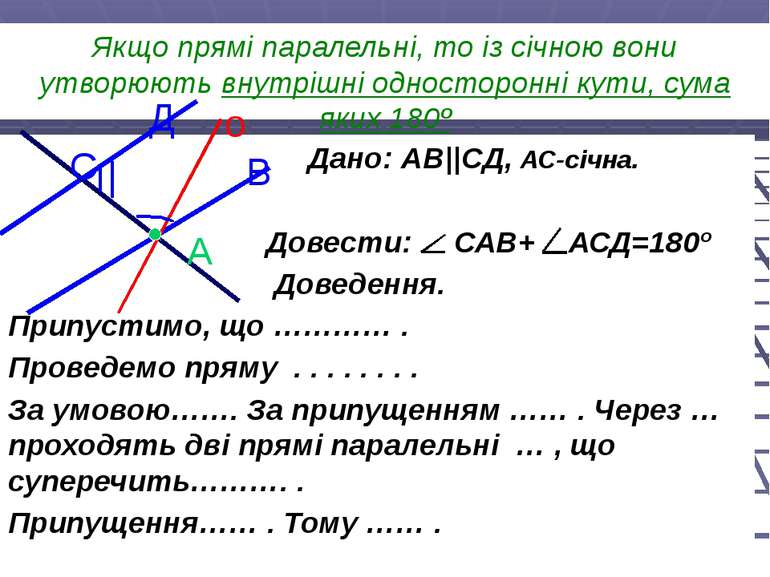
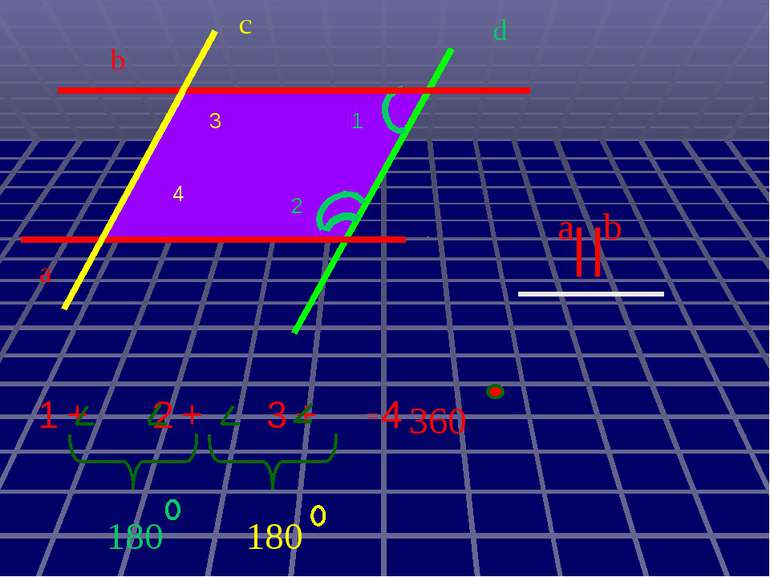
Якщо прямі паралельні, то із січною вони утворюють внутрішні односторонні кути, сума яких 180º Дано: АВ||СД, АС-січна. Довести: САВ+ АСД=180º Доведення. Припустимо, що ………… . Проведемо пряму . . . . . . . . За умовою……. За припущенням …… . Через … проходять дві прямі паралельні … , що суперечить………. . Припущення…… . Тому …… . Д о С В А

Поновити сили. Спортивна зупинка ЗУПИНКА ДОВЕДЕНЬ Довести одну з властивостей кутів... Ознайомитися з методом доведення від супротивного.

ЗУПИНКА ЗАКРІПЛЕННЯ ЗНАНЬ Повторити і застосувати властивості кутів…

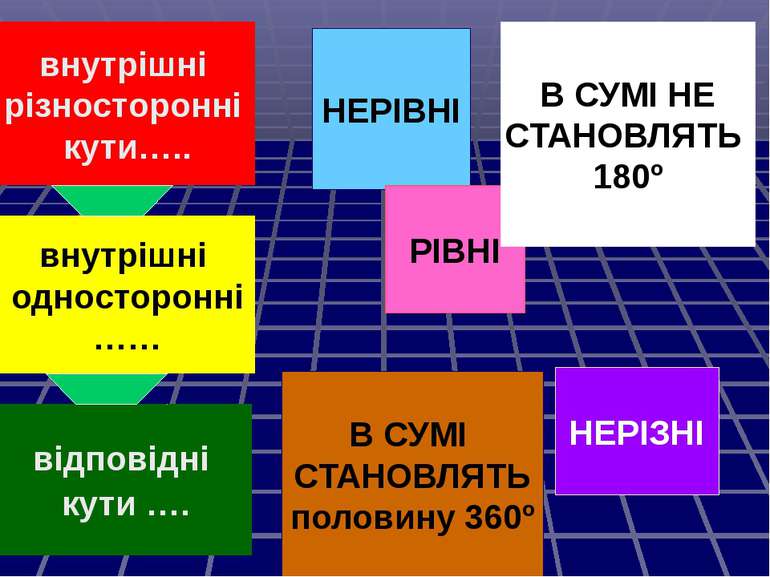
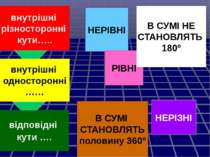
внутрішні різносторонні кути….. внутрішні односторонні …… відповідні кути …. НЕРІВНІ В СУМІ СТАНОВЛЯТЬ половину 360º РІВНІ В СУМІ НЕ СТАНОВЛЯТЬ 180º НЕРІЗНІ

а b с 1 2 3 4 5 8 7 6 b а

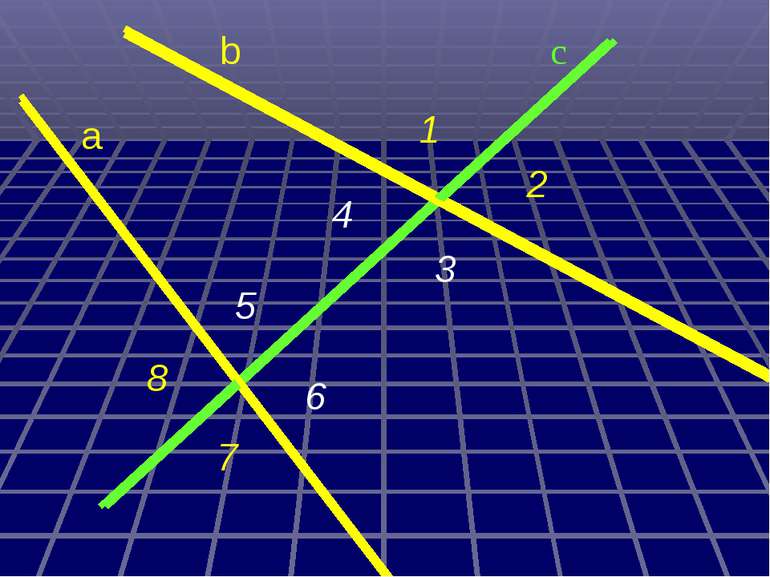
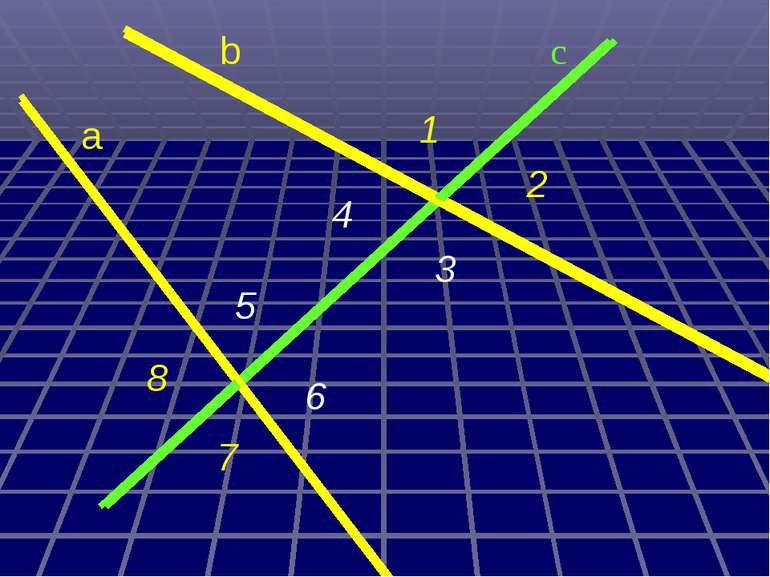
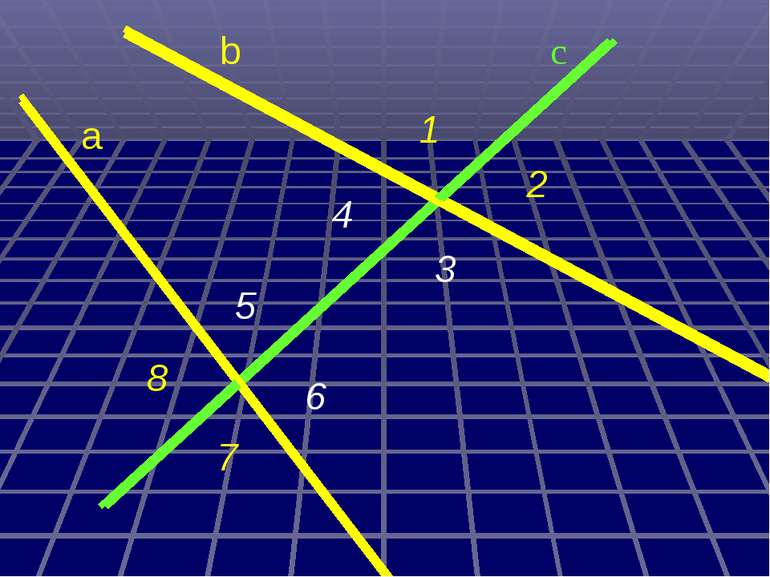
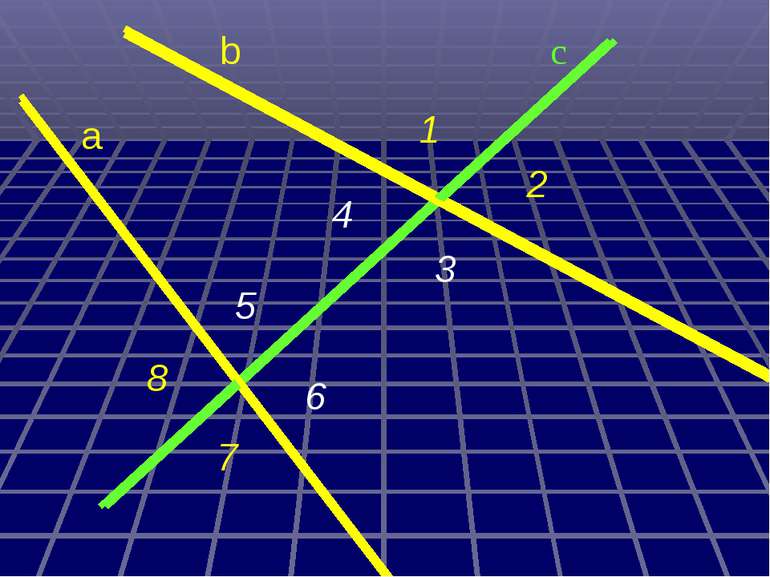
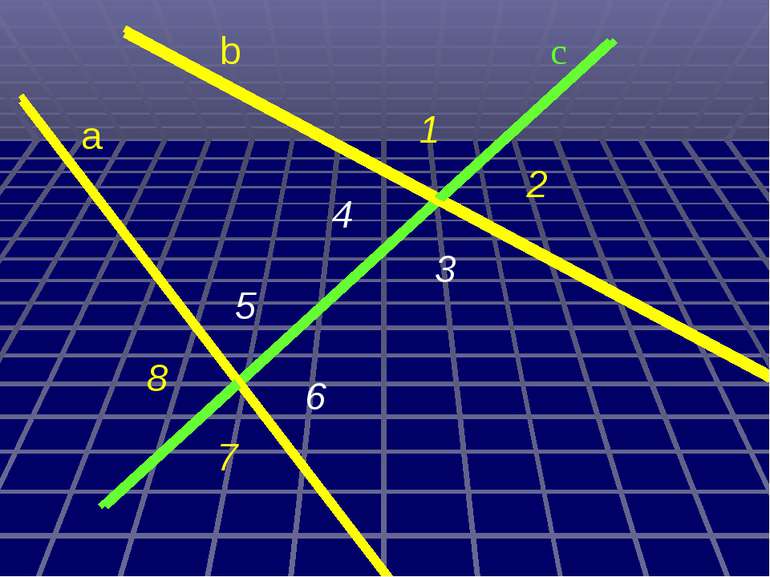
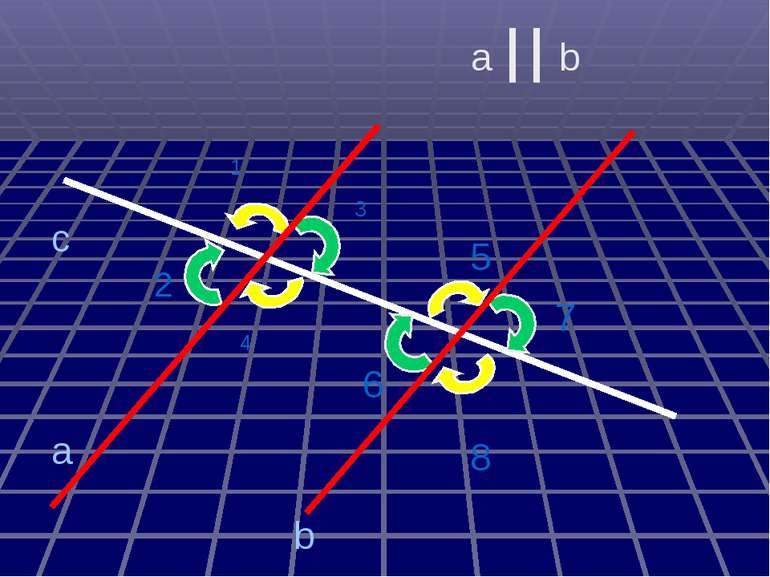
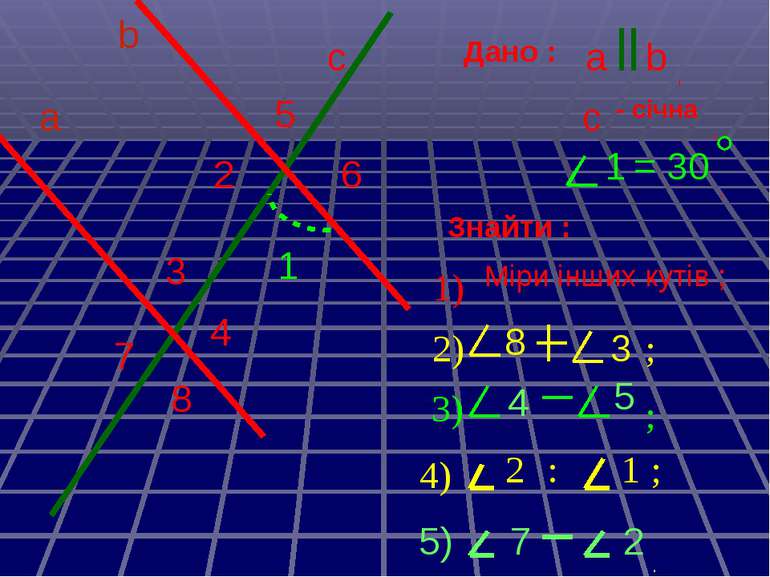
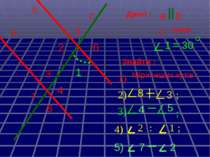
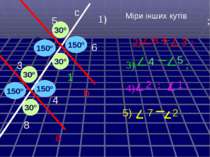
а с b 6 5 4 3 2 1 8 7 Міри інших кутів ; 1) 3) 8 4 5 3 . b а ; ; ; 4) 2 2) 5) 7 1 2 : Дано : с - січна , , 1 = 30 . Знайти :

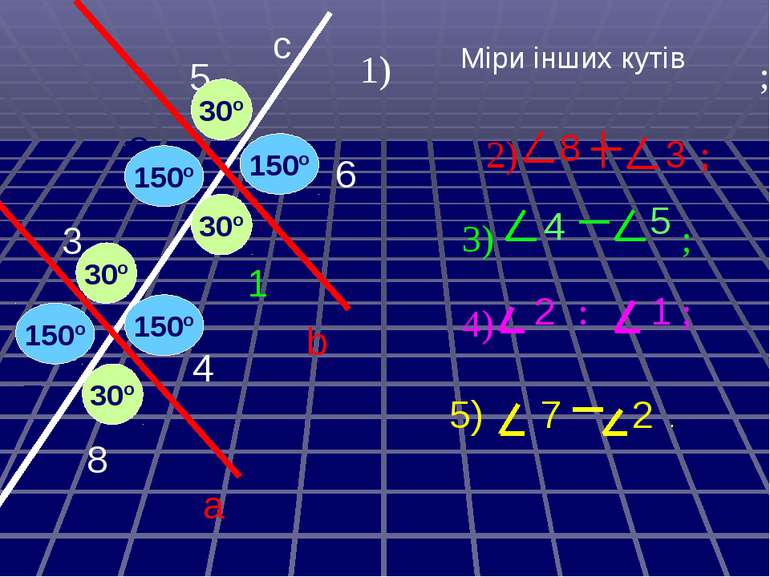
а с b 6 5 4 3 2 1 8 7 30º 30º 30º 30º 150º 150º 150º 150º Міри інших кутів 1) 3) 8 4 5 3 . ; ; ; ; 4) 2 2) 5) 7 1 2 :

Стор.59. №198.

Дано: а||b, с - січна 1 = 30º Знайти: 2, 3, 4, 5, 6, 7, 8. Розв´язання. 1= 4 = 30º (властивість внутрішніх різносторонніх кутів) 1= 5= 30º і 4= 6= 30º (властивість внутрішніх відповідних кутів) 1+ 3=180º (властивість внутрішніх односторонніх кутів) 3=180 º- 1=180 º-30 º=150 º 3= 7=150 º(властивість внутрішніх різносторонніх кутів) 3= 8=150 º і 7= 2=150 º (властивість внутрішніх відповідних кутів) Відповідь: 4= 5= 6=30 º, 2= 3= 7= 8=150 º. 1 2 3 4 5 7 6 8

ВІРЮ - НЕ ВІРЮ ? ? ? ? ? ? ?

1. Паралельні прямі на площині – це прямі, які не перетинаються. 2. Якщо, мені потрібно довести, що дві прямі паралельні – я згадую властивості кутів утворених січною з паралельними прямими. Через точку , яка не належить прямій, можна провести безліч паралельних їй прямих. Якщо у результаті перетину паралельних прямих січною утворилися два кути по 80º. Можуть вони бути: відповідними; внутрішніми односторонніми; внутрішніми різносторонніми?

5. Якщо, мені потрібно довести, що дві прямі паралельні – я згадую ознаки паралельності прямих. 6. Якщо один із відповідних кутів гострий, то інший тупий. 7. Якщо один із внутрішніх односторонніх кутів гострий, то інший тупий.

8. Якщо сума внутрішніх різносторонніх кутів 140º, то один із них 70º. 9. Якщо один із внутрішніх односторонніх кутів удвічі більший за другий, то їх градусна міра : 30º і 60º. 10. Якщо один із внутрішніх кутів прямий, то інші теж прямі.

1. Домашнє завдання: Опрацювати § 7(сторінка 55-56) № 198, 200 , 216*, дослідити зовнішні кути. 2. Чи досягли ми мети? 3. На якій зупинці ви хотіли б опинитися ще раз? 4. Хто , на вашу думку, працював найкраще ? ПІДСУМКОВА ЗУПИНКА

ПІДГОТОВЧА ЗУПИНКА ДОСЛІДНИЦЬКА ЗУПИНКА ІСТОРИЧНА ЗУПИНКА ЗУПИНКА ДОВЕДЕНЬ ЗУПИНКА ЗАКРІПЛЕНЬ ПІДСУМКОВА ЗУПИНКА

1 2 3 4 1+ 2+ 3+ 4 = а b c d 180 180 360 а b

1 2 3 4 5 = a b c d 1 3 + + + + 5 5 4 2 = 180 ? а b

Ми закінчили урок! Пролунав уже дзвінок!