Презентація на тему:
Відстані у просторі

Відстані в просторі

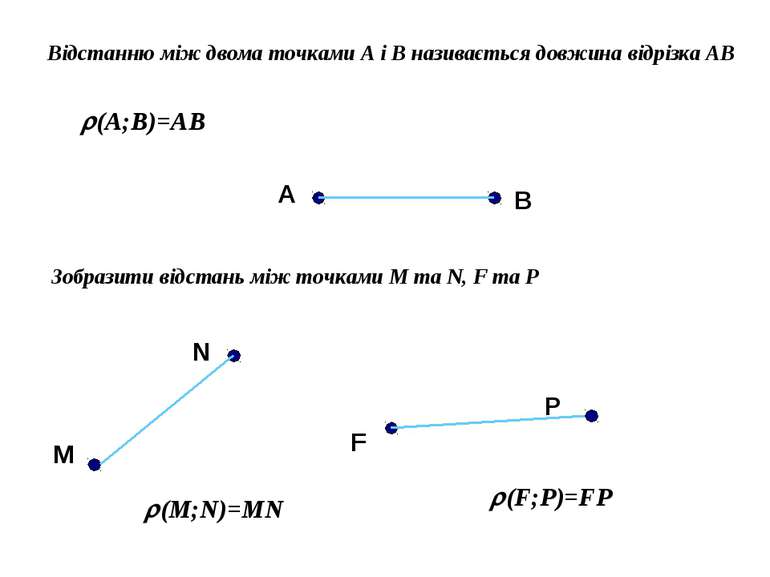
Відстанню між двома точками А і В називається довжина відрізка АВ (A;B)=AB А В Зобразити відстань між точками M та N, F та Р M N F P (M;N)=MN (F;P)=FP

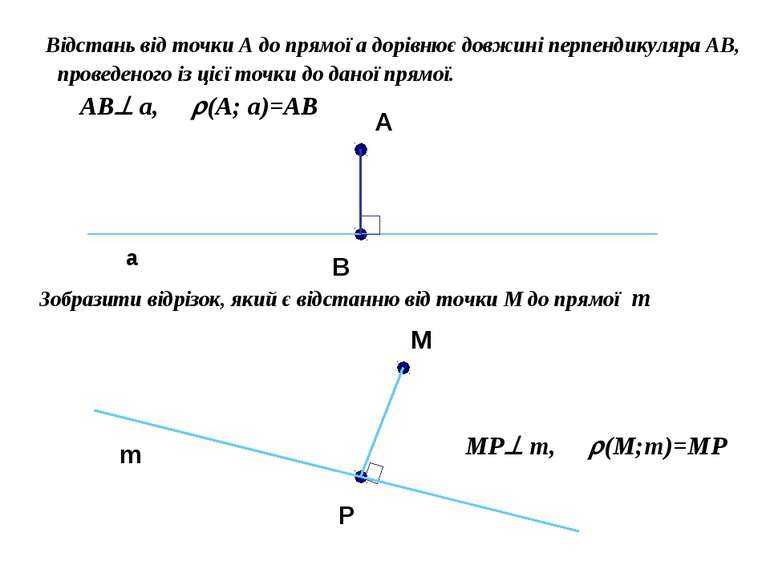
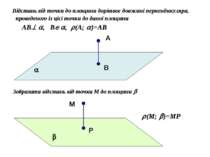
Відстань від точки А до прямої a дорівнює довжині перпендикуляра АВ, проведеного із цієї точки до даної прямої. AB a, (A; a)=AB А a Зобразити відрізок, який є відстанню від точки M до прямої m M m P В MP m, (M;m)=MP

Відстанню від точки А до відрізка ВС є найкоротший з відрізків, що сполучають задану точку А з точкою цього відрізка. А О ? Відстань від точки А до відрізка ВС визначають за таким алгоритмом: 1) проводимо перпендикуляр АО на пряму ВС; 2) якщо основа О цього перпендикуляра належить даному відрізку ВС, то шукана відстань дорівнює довжині відрізка АО; 3) в іншому випадку вона дорівнює довжині відрізка АВ чи АС (залежно від того, яка з точок В чи С лежить ближче до точки О)

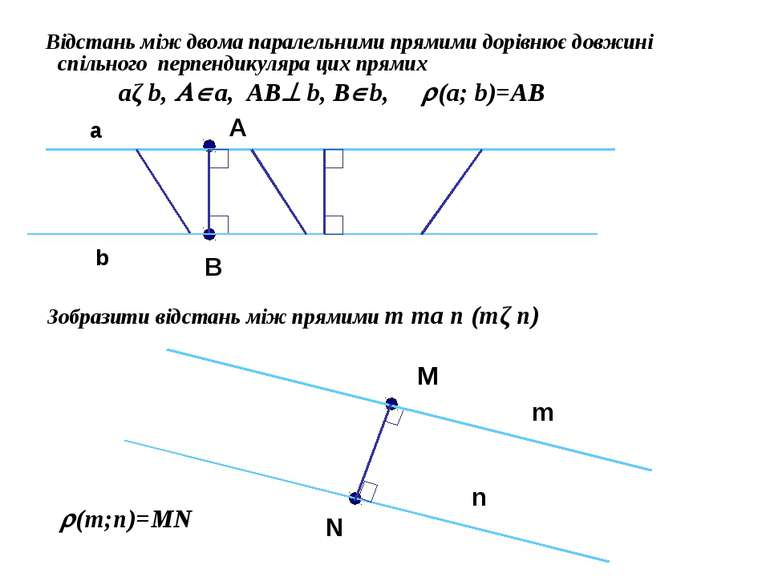
Відстань між двома паралельними прямими дорівнює довжині спільного перпендикуляра цих прямих aǁb, a, AB b, B b, (a; b)=AB А a Зобразити відстань між прямими m та n (mǁn) M m N В b n (m;n)=MN

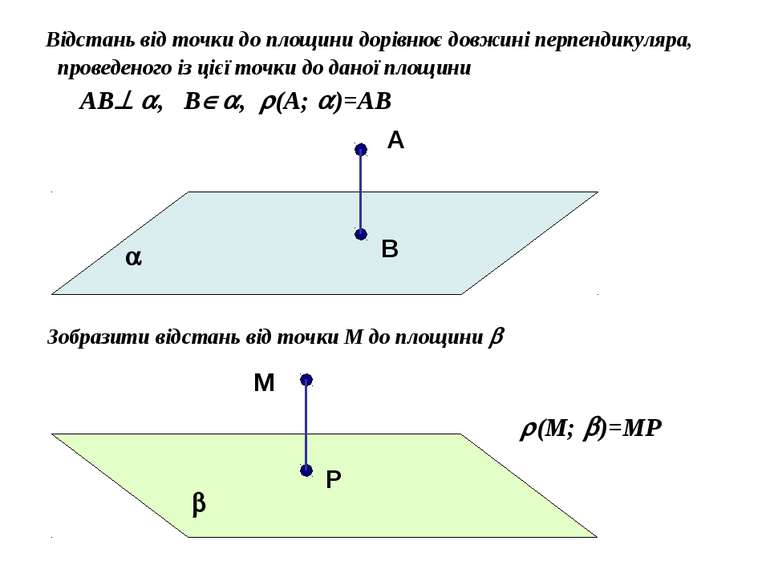
Відстань від точки до площини дорівнює довжині перпендикуляра, проведеного із цієї точки до даної площини AB , B , (A; )=AB А Зобразити відстань від точки M до площини M P В (M; )=MP

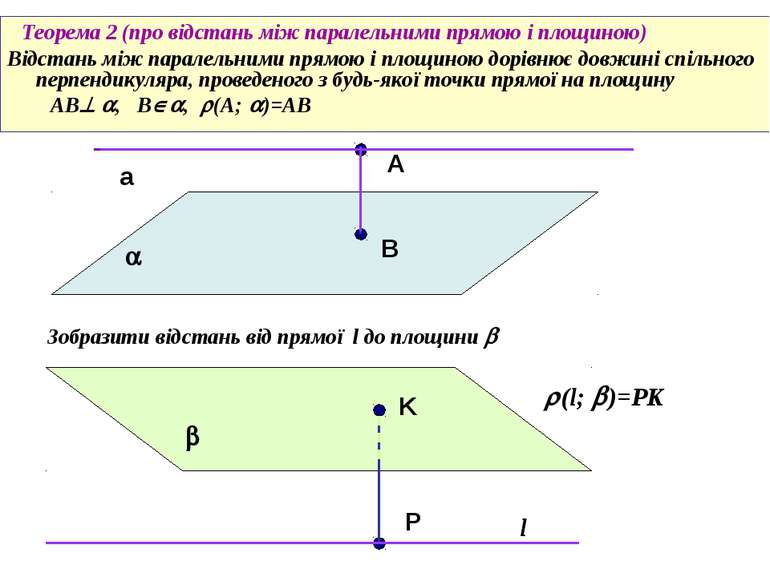
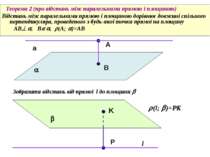
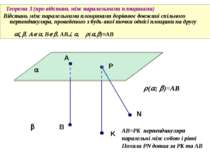
Теорема 2 (про відстань між паралельними прямою і площиною) Відстань між паралельними прямою і площиною дорівнює довжині спільного перпендикуляра, проведеного з будь-якої точки прямої на площину AB , B , (A; )=AB А Зобразити відстань від прямої l до площини l P В (l; )=PK a K

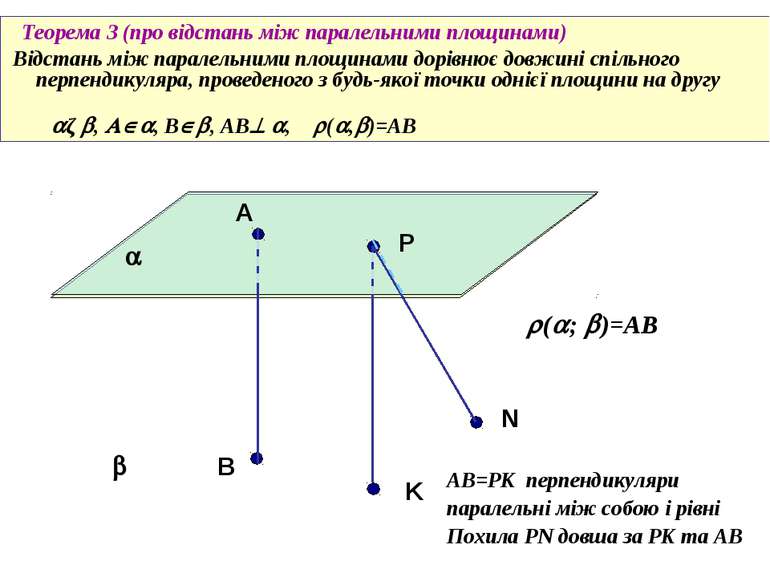
Теорема 3 (про відстань між паралельними площинами) Відстань між паралельними площинами дорівнює довжині спільного перпендикуляра, проведеного з будь-якої точки однієї площини на другу ǁ , , B , AB , ( , )=AB А P В ( ; )=AB K N AB=РК перпендикуляри паралельні між собою і рівні Похила PN довша за PK та AB

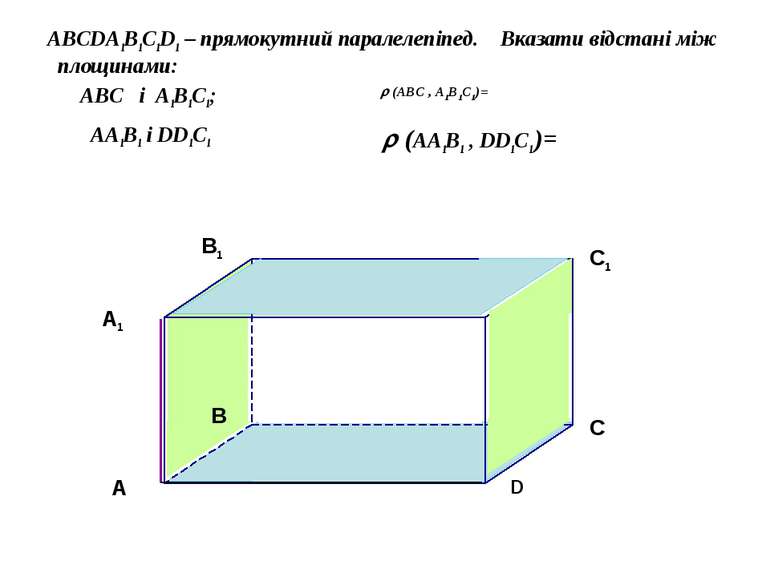
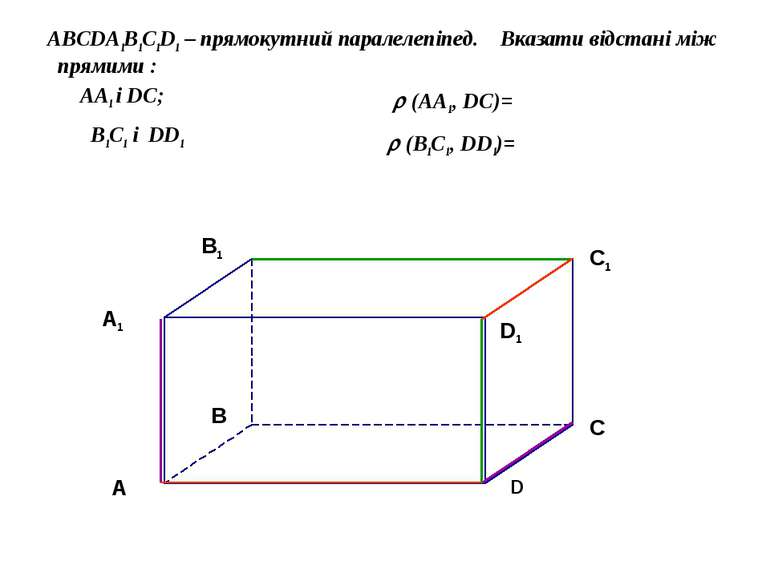
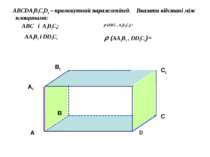
ABCDA1B1C1D1 – прямокутний паралелепіпед. Вказати відстані між площинами: ABC і A1B1С1; AA1B1 і DD1C1 (ABC , A1B1С1)= (AA1B1 , DD1C1 )=

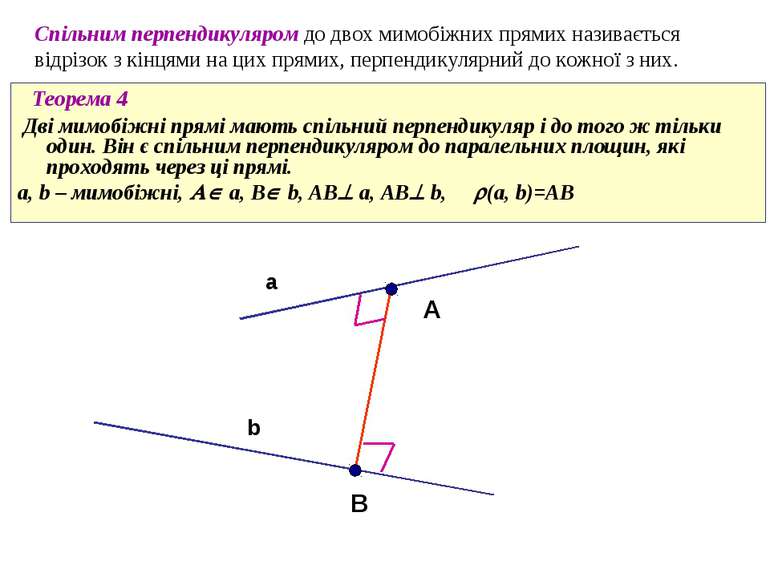
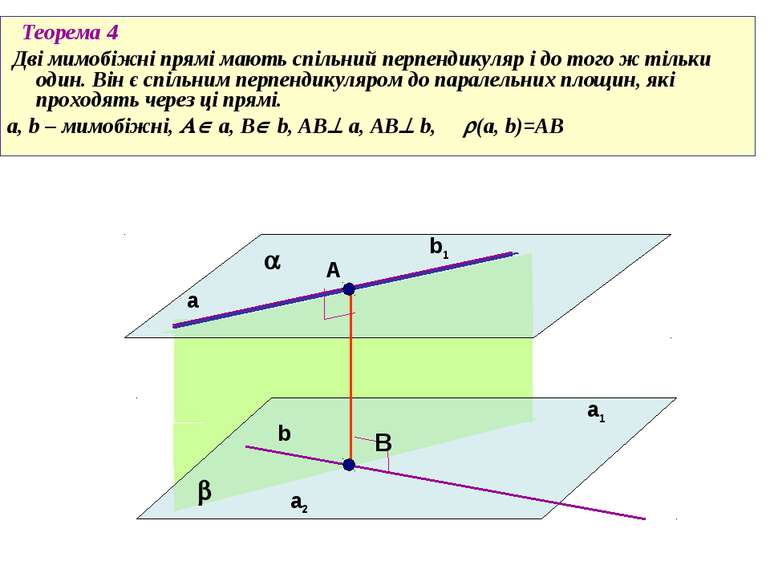
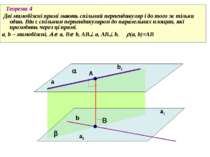
Cпільним перпендикуляром до двох мимобіжних прямих називається відрізок з кінцями на цих прямих, перпендикулярний до кожної з них. a b А В Теорема 4 Дві мимобіжні прямі мають спільний перпендикуляр і до того ж тільки один. Він є спільним перпендикуляром до паралельних площин, які проходять через ці прямі. a, b – мимобіжні, a, B b, AB a, AB b, (a, b)=AB

Теорема 4 Дві мимобіжні прямі мають спільний перпендикуляр і до того ж тільки один. Він є спільним перпендикуляром до паралельних площин, які проходять через ці прямі. a, b – мимобіжні, a, B b, AB a, AB b, (a, b)=AB a b a1 b1 a2 В А

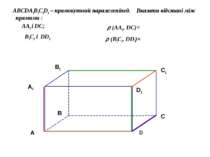
ABCDA1B1C1D1 – прямокутний паралелепіпед. Вказати відстані між прямими : AA1 і DС; B1C1 і DD1 (AA1 , DС)= (B1C1 , DD1)=