Презентація на тему:
Теорема про три перпендикуляри

Тема: Теорема о трех перпендикулярах.

Тема: Теорема о трех перпендикулярах. Цели: изучение теоремы (доказательство теоремы разными способами); формирование навыков решения задач с использованием теоремы; развитие логической культуры учащихся. Тип урока: получение новых знаний. Оборудование: мультимедийная доска, ПК, карточки с заданиями, учебник.

На этом уроке учащиеся ознакомятся с важными теоретическими знаниями, которые они смогут применять для нахождения расстояния от точки до прямой в пространстве. Организационный момент. Формирование цели и задачи урока, мотивация учебной деятельности. Как найти расстояние от точки А до прямой а? А

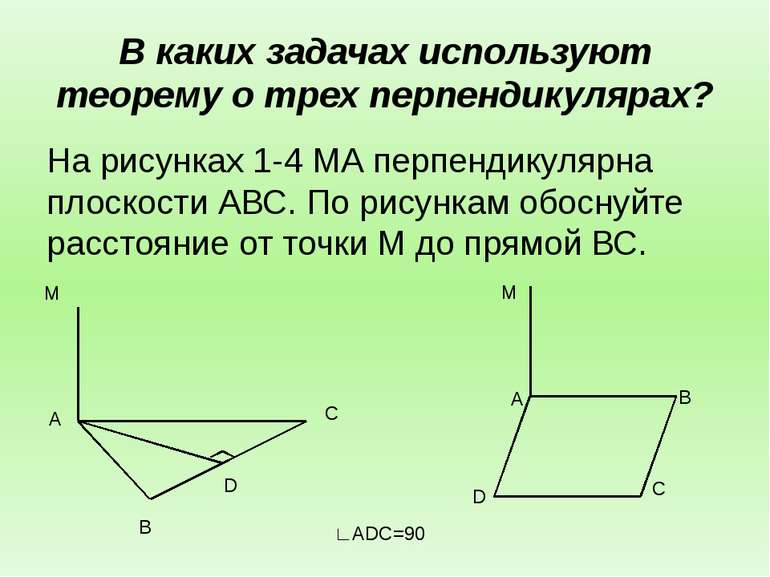
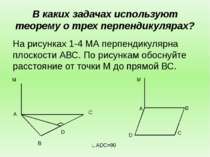
В каких задачах используют теорему о трех перпендикулярах? На рисунках 1-4 МА перпендикулярна плоскости АВС. По рисункам обоснуйте расстояние от точки М до прямой ВС. A B D C M M A B C D ∟ADC=90

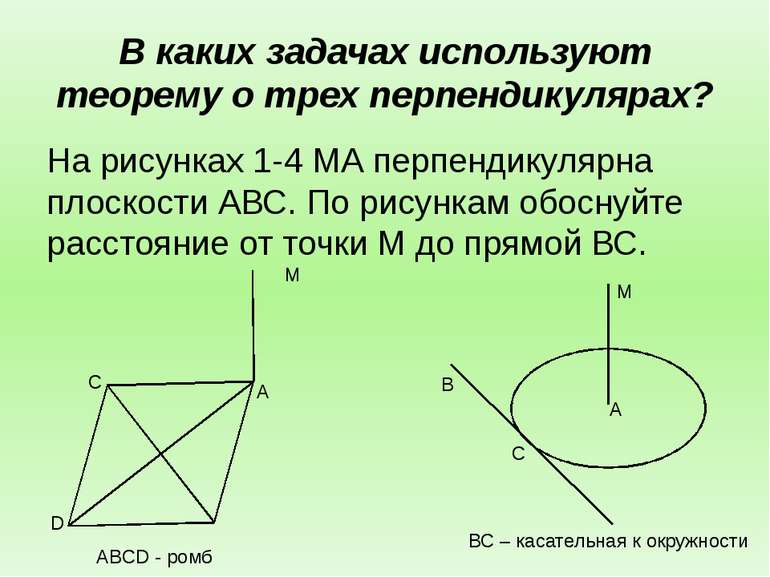
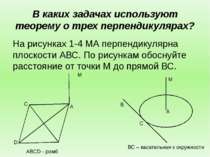
В каких задачах используют теорему о трех перпендикулярах? На рисунках 1-4 МА перпендикулярна плоскости АВС. По рисункам обоснуйте расстояние от точки М до прямой ВС. D C A M ABCD - ромб A C B M ВС – касательная к окружности

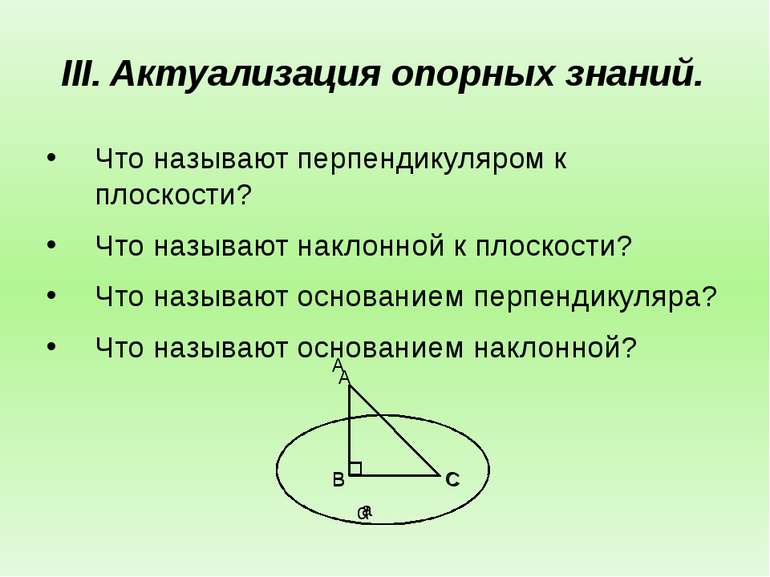
Актуализация опорных знаний. Что называют перпендикуляром к плоскости? Что называют наклонной к плоскости? Что называют основанием перпендикуляра? Что называют основанием наклонной? A B C a А B C α

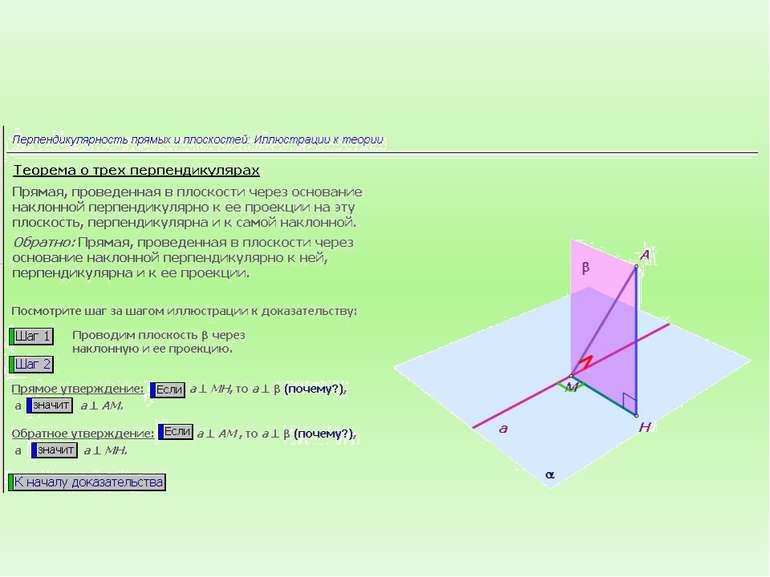
Восприятие нового материала. Теорема: если прямая, лежащая в плоскости, перпендикулярна проекции наклонной, то эта прямая перпендикулярна наклонной. Доказательство теоремы проводится с использованием программы «УМК живая математика»

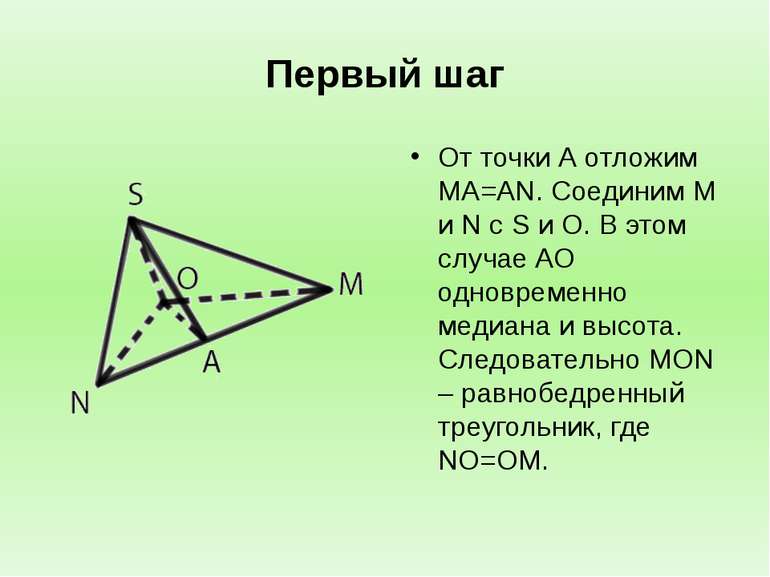
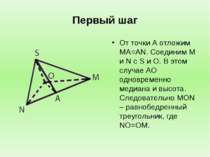
Первый шаг От точки А отложим MA=AN. Соединим M и N с S и O. В этом случае AO одновременно медиана и высота. Следовательно MON – равнобедренный треугольник, где NO=OM.

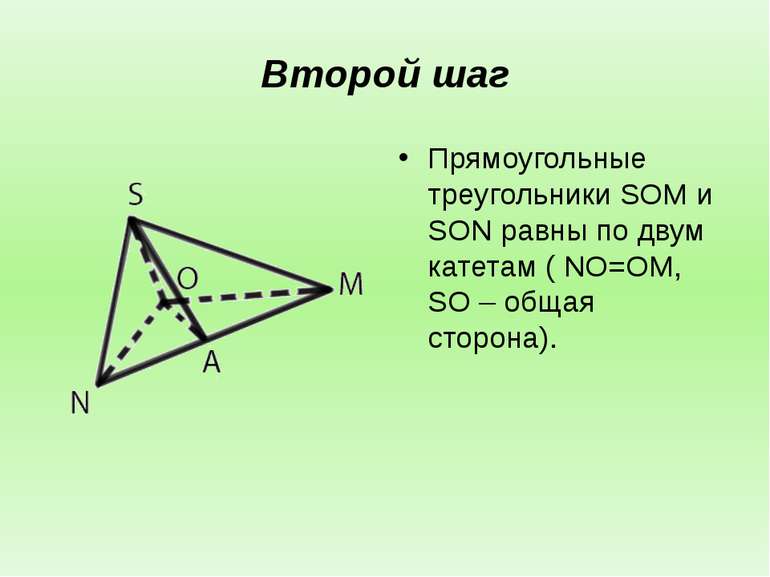
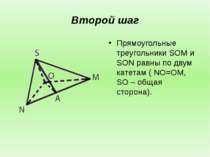
Второй шаг Прямоугольные треугольники SOM и SON равны по двум катетам ( NO=OM, SO – общая сторона).

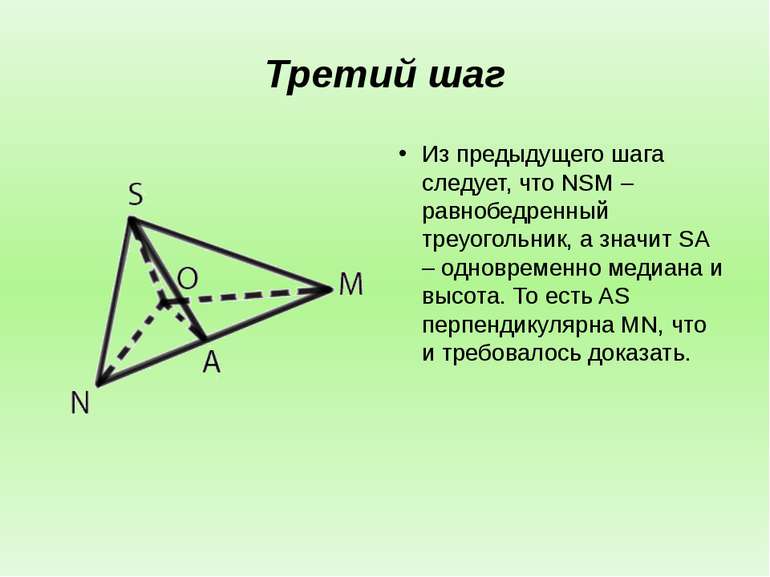
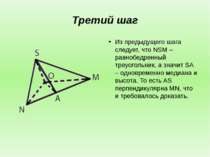
Третий шаг Из предыдущего шага следует, что NSM – равнобедренный треуогольник, а значит SA – одновременно медиана и высота. То есть AS перпендикулярна MN, что и требовалось доказать.

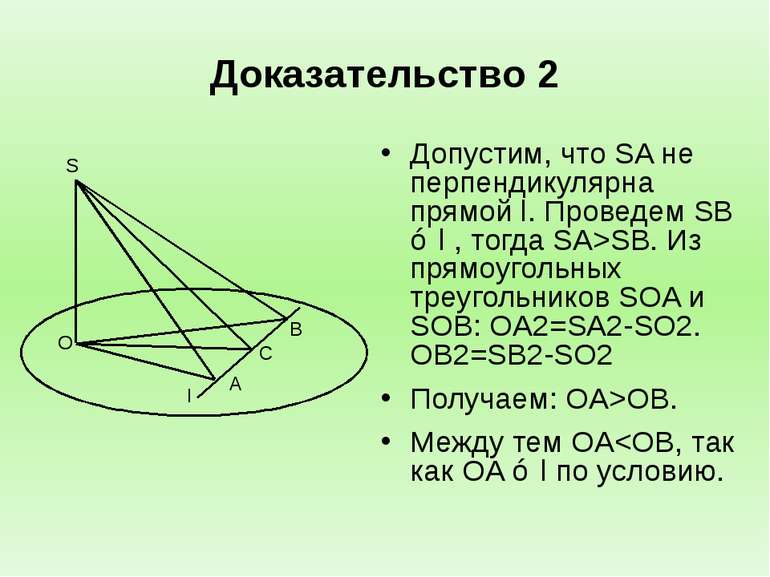
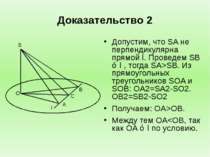
Доказательство 2 Допустим, что SA не перпендикулярна прямой l. Проведем SB ⊥ l , тогда SA>SB. Из прямоугольных треугольников SOA и SOB: OA2=SA2-SO2. OB2=SB2-SO2 Получаем: OA>OB. Между тем OA

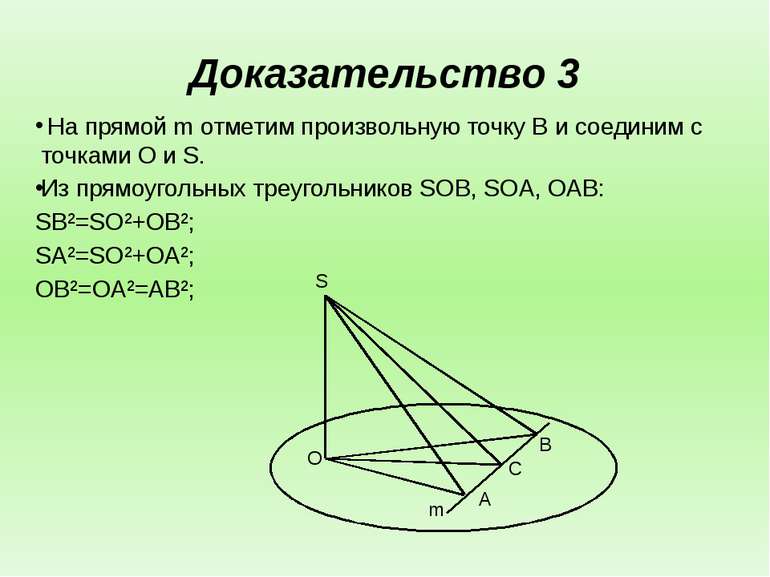
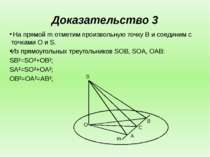
Доказательство 3 На прямой m отметим произвольную точку B и соединим с точками O и S. Из прямоугольных треугольников SOB, SOA, OAB: SB²=SO²+OB²; SA²=SO²+OA²; OB²=OA²=AB²; S O B C A m

Доказательство 3 Вычтя почленно из первого равенства второе, получим: SB²=SA²=OB²=OA² Приняв во внимание третье равенство, будем иметь: SB²=SA²=AB². SB²=SA²+AB². Согласно обратной теореме Пифагора: SA ⊥ AB , т.е. m ⊥ SA.

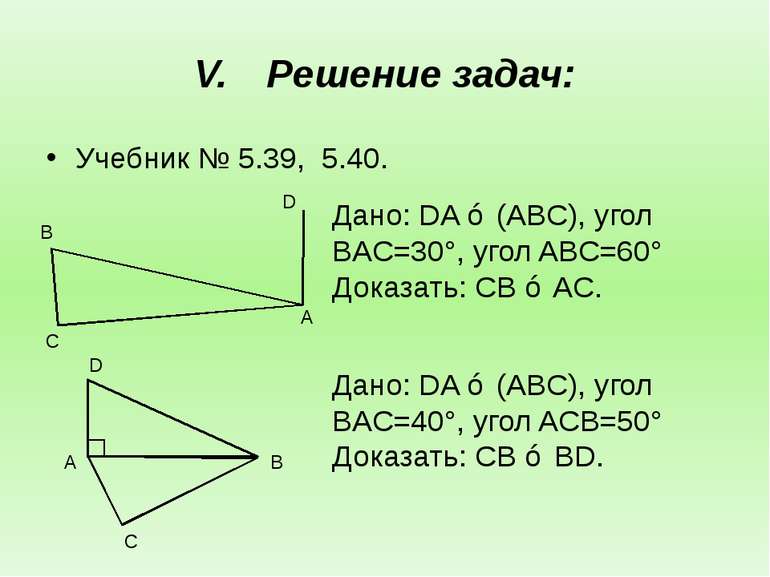
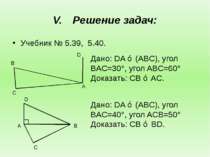
Решение задач: Учебник № 5.39, 5.40. Дано: DA ⊥ (ABC), угол BAC=30°, угол ABC=60° Доказать: СВ ⊥ AC. Дано: DA ⊥ (ABC), угол BAC=40°, угол ACB=50° Доказать: СВ ⊥ BD. D А B D C

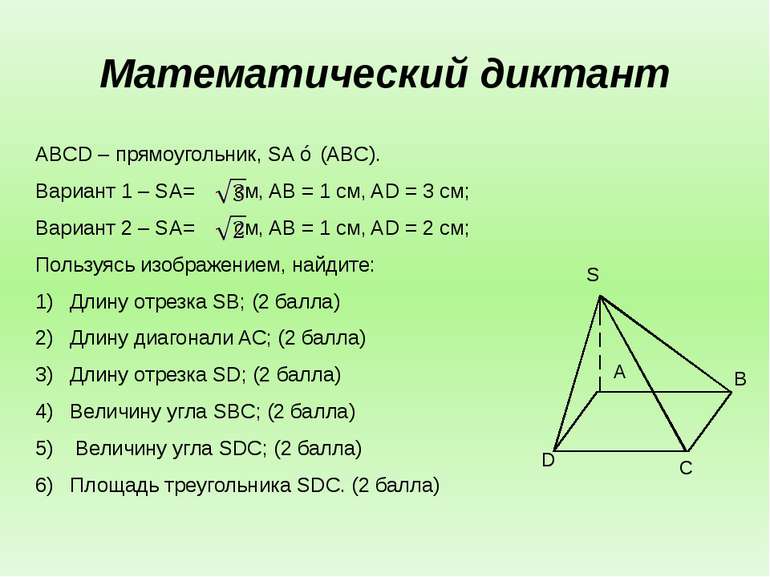
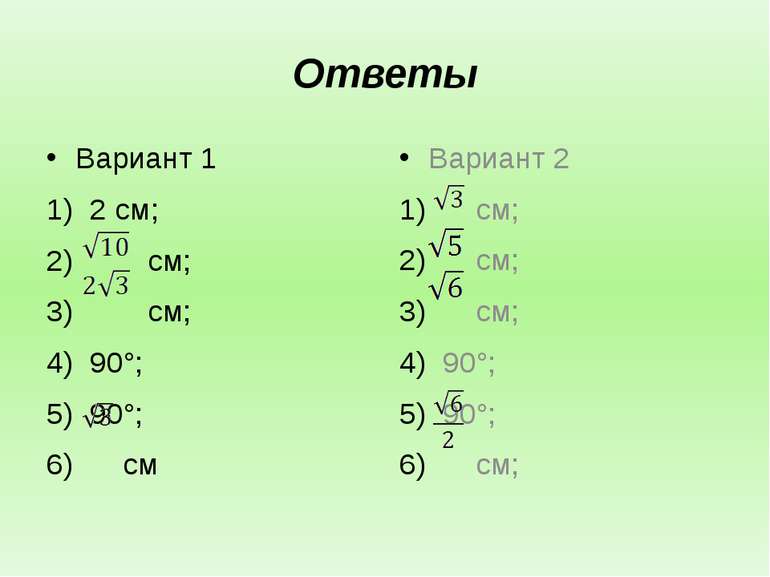
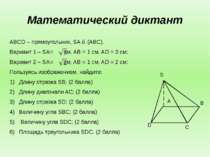
Математический диктант ABCD – прямоугольник, SA ⊥ (ABC). Вариант 1 – SA= см, AB = 1 см, AD = 3 см; Вариант 2 – SA= см, AB = 1 см, AD = 2 см; Пользуясь изображением, найдите: Длину отрезка SB; (2 балла) Длину диагонали AC; (2 балла) Длину отрезка SD; (2 балла) Величину угла SBC; (2 балла) Величину угла SDC; (2 балла) Площадь треугольника SDC. (2 балла) B С D A S

Ответы Вариант 1 2 см; см; см; 90°; 90°; см Вариант 2 см; см; см; 90°; 90°; см;

Домашнее задание: § 5.3, теорема. N 5.63 – учебник. «Разноуровневые дидактические материалы» под редакцией А.П. Ершовой. С-10 по вариантам уровни: А N 1; 2. Б N 3

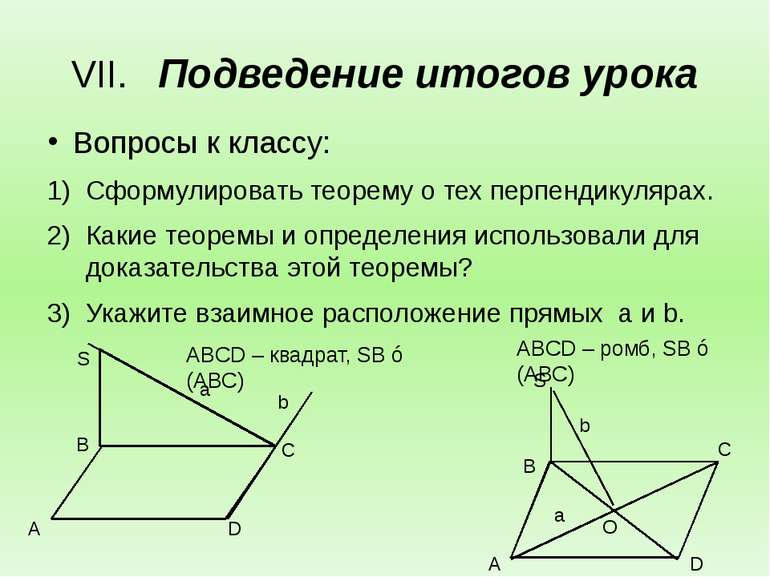
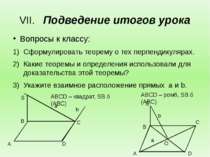
Подведение итогов урока Вопросы к классу: Сформулировать теорему о тех перпендикулярах. Какие теоремы и определения использовали для доказательства этой теоремы? Укажите взаимное расположение прямых a и b. ABCD – квадрат, SB ⊥ (ABC) ABCD – ромб, SB ⊥ (ABC) a b O a S

Спасибо за внимание!