Презентація на тему:
ПІФАГОР

Піфагор

Не роби ніколи того, що не знаєш. Але вчись усьому, що потрібно знати, і тоді будеш вести спокійне життя. Піфагор

Піфагор (580 - 500 рр.до н.е.) Давньогрецький філософ, релігійний та політичний діяч, засновник піфагореїзму.

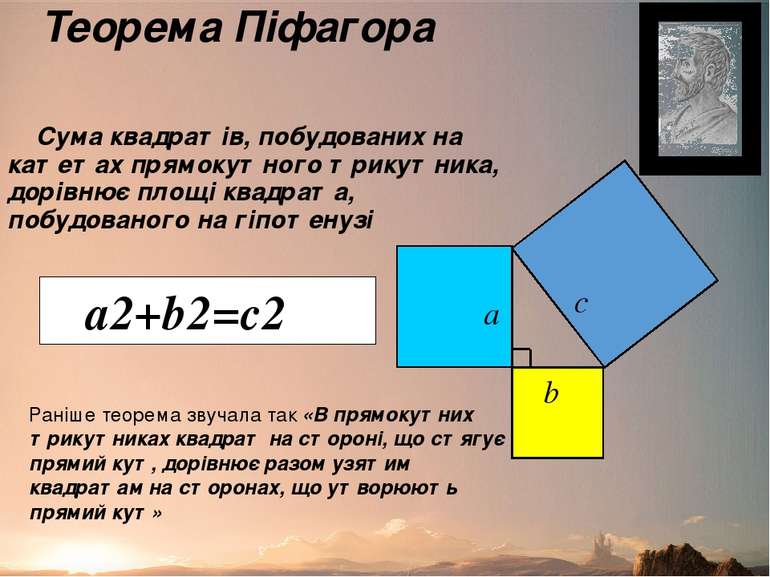
Теорема Піфагора Сума квадратів, побудованих на катетах прямокутного трикутника, дорівнює площі квадрата, побудованого на гіпотенузі а c b а2+b2=с2 Раніше теорема звучала так «В прямокутних трикутниках квадрат на стороні, що стягує прямий кут, дорівнює разом узятим квадратам на сторонах, що утворюють прямий кут»

"Піфагорові штани на всі боки рівні". Такі гасла придумували учні середніх століть при вивченні теореми; малювали шаржі. Наприклад, такі:

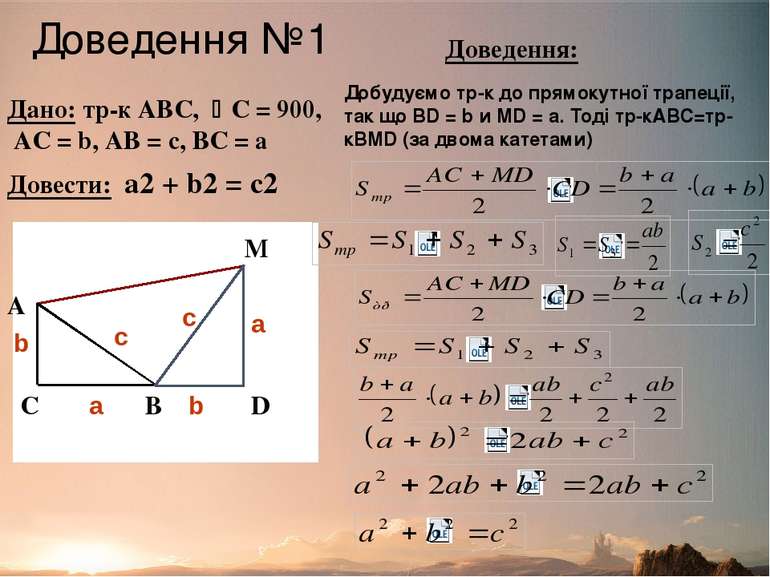
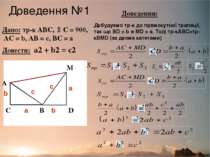
Доведення №1 Дано: тр-к АВС, C = 900, AC = b, AB = c, BC = a Довести: a2 + b2 = c2 Добудуємо тр-к до прямокутної трапеції, так що BD = b и MD = a. Тоді тр-кABC=тр-кBMD (за двома катетами) Доведення:

Доведення №2 («Дивись») В квадраті зі стороною a+b зображали чотири прямокутних трикутники з катетами a і b і писали «Дивись». І дійсно, поглянувши на ці малюнки, бачимо, що зліва вільна від трикутників фігура, складається з двох квадратів зі сторонами a і b і відповідно її площа, a2 + b2, а справа квадрат зі стороною с. Його площа с2. Маємо рівність a2 + b2= с2 Очевидно факт, викладений в теоремі Піфагора був спочатку встановлений для рівнобедреного прямокутного трикутника. Достатньо поглянути на мозаїку, щоб переконатися в справедливості теореми для трикутника АВС.

Доведення №3 (індійське доведення) Площа великого квадрата Sв. квадрата = с2 Sв. квадрата = 4Sтрикутника +S м. квадрата Sв. квадрата = 4 ½ ab + (a-b)2 2ab + a2 – 2ab+ b2= с2 a2 + b2= с2

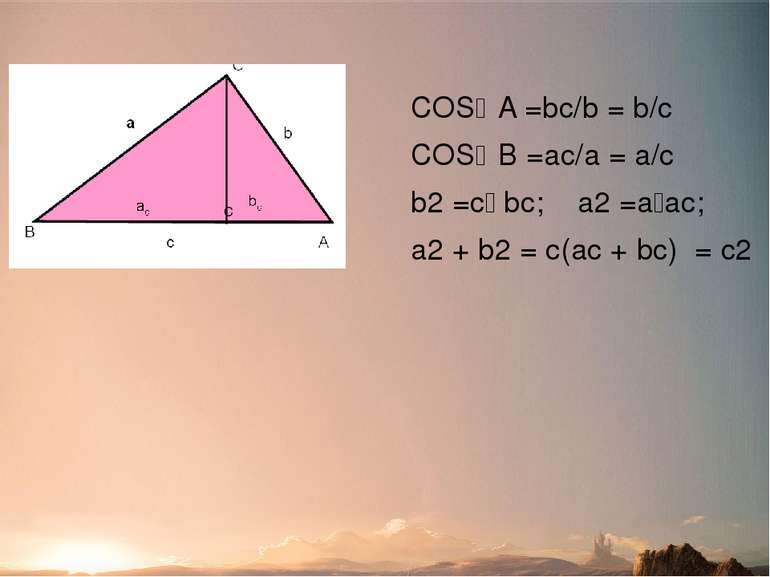
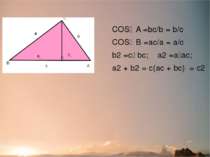
Доведення №4 (за допомогою тригонометричних функцій) COS A =bc/b = b/c COS B =ac/a = a/c b2 =c bc; a2 =a ac; a2 + b2 = с(ac + bc) = c2 C

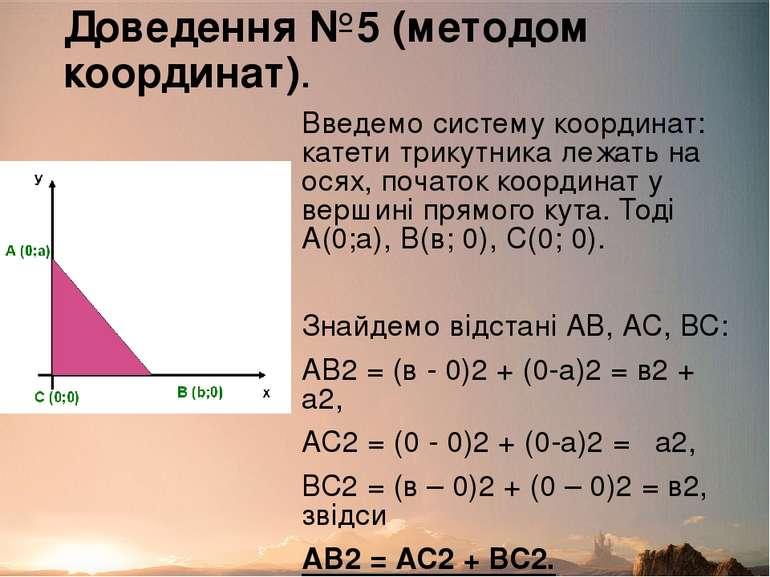
Доведення №5 (методом координат). Введемо систему координат: катети трикутника лежать на осях, початок координат у вершині прямого кута. Тоді А(0;а), В(в; 0), С(0; 0). Знайдемо відстані АВ, АС, ВС: АВ2 = (в - 0)2 + (0-а)2 = в2 + а2, АС2 = (0 - 0)2 + (0-а)2 = а2, ВС2 = (в – 0)2 + (0 – 0)2 = в2, звідси АВ2 = АС2 + ВС2.

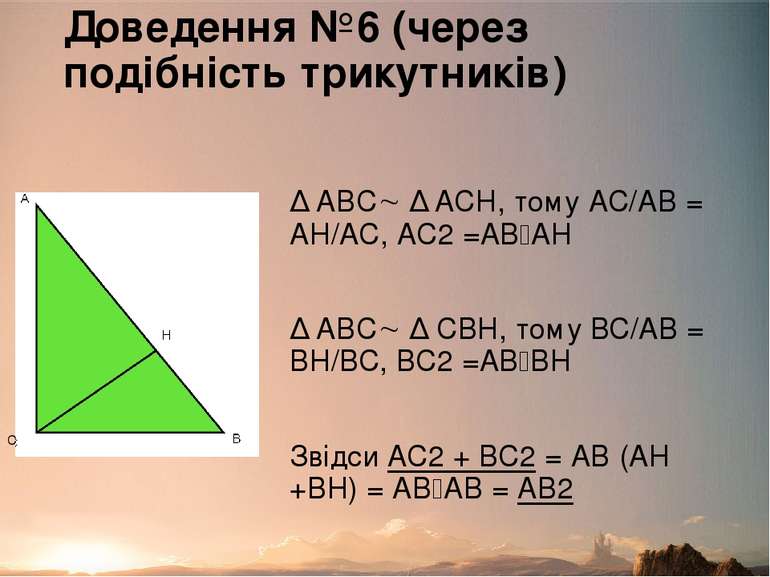
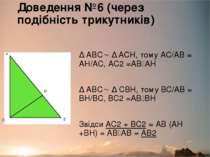
Доведення №6 (через подібність трикутників) ∆ ABC ∆ ACH, тому АС/АВ = АН/АС, АС2 =АВ АН ∆ ABC ∆ СВH, тому ВС/АВ = ВН/ВС, ВС2 =АВ ВН Звідси АС2 + ВС2 = АВ (АН +ВН) = АВ АВ = АВ2 C

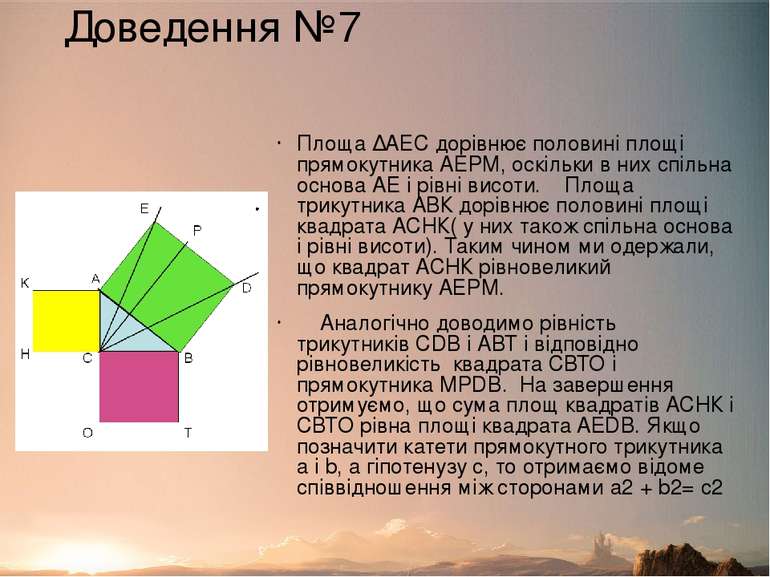
Доведення №7 Площа ∆АЕС дорівнює половині площі прямокутника АЕРМ, оскільки в них спільна основа АЕ і рівні висоти. Площа трикутника АВК дорівнює половині площі квадрата АСНК( у них також спільна основа і рівні висоти). Таким чином ми одержали, що квадрат АСНК рівновеликий прямокутнику АЕРМ. Аналогічно доводимо рівність трикутників CDB і АВТ і відповідно рівновеликість квадрата СВТО і прямокутника MPDB. На завершення отримуємо, що сума площ квадратів АСНК і СВТО рівна площі квадрата AEDB. Якщо позначити катети прямокутного трикутника a і b, а гіпотенузу с, то отримаємо відоме співвідношення між сторонами a2 + b2= с2

Єгипетський трикутник Єгипетський трикутник — прямокутний трикутник зі співвідношенням сторін 3:4:5. Особливістю такого трикутника, відомою ще з античних часів, є те, що всі його сторони є цілочисельні, а згідно теореми, оберненої до теореми Піфагора, він є прямокутним. Єгипетський трикутник є найпростішим (і першим відомим) з Геронових трикутників — трикутників з цілочисельними сторонами і площами. Радіус вписаного в трикутник кола рівний одиниці. Назву трикутнику з таким співвідношенням сторін дали елліни: в VII-V століттях до н.е. грецькі філософи і суспільні діячі активно відвідували Єгипет. Так, наприклад, Піфагор в 535 р. до н.е. за наполяганням Фалеса для вивчення астрономії і математики відправився в Єгипет - і, судячи з усього, саме спроба узагальнення співвідношення квадратів, характерного для єгипетського трикутника, на будь-які прямокутні трикутники і привела Піфагора до доведення його знаменитої теореми. Сума зазначених чисел (3+4+5=12) із давніх часів використовувалася як одиниця кратності при побудові прямих кутів за допомогою мотузки, розміченої вузлами на 3/12 й 7/12 її довжини. Застосовувався єгипетський трикутник в середньовічній архітектурі для побудови схем пропорційності. Сторони єгипетського трикутника утворюють найпростішу піфагорову трійку — 32+42=52.

1. Про яке число єгиптяни говорили, що воно має божественну властивість і чому? Число 5, бо його квадрат дорівнює сумі квадратів двох попередніх чисел. 2. У піфагорійців самою страшною клятвою вважалась клятва числом … Чому? 36: дорівнює сумі перших чотирьох парних і перших чотирьох непарних чисел; сумі кубів трьох перших натуральних чисел. 3. Яке відкриття в школі Піфагора призвело до першої кризи в математиці? Несумісність сторони квадрата і його діагоналі (не кожен відрізок має довжину, що вимірюється цілим числом). 4. Чи можна побудувати прямокутний трикутник, у якого всі сторони є непарними числами? Ні, сума квадратів двох непарних чисел є число парне 5. Які числа називають піфагоровими? Трійки натуральних чисел, що мають властивість a2 + b2= с2. 6. Чи можна з 36 сірників, не ламаючи їх скласти прямокутний трикутник? Можна, 3n +4n +5n =36. 7. Якось Піфагора запитали: «Скільки учнів навчається у тебе в школі?». Він відповів: «Половина вивчає математику, четверта частина – музику, сьома – мовчить і ще є три жінки» 28 учнів. 8. Є мотузка, поділена вузликами на 12 рівних частин Для чого використовувалася така мотузка в Древньому Єгипті? Для побудови прямих кутів. 9. Що, в перекладі з грецької означають терміни: гіпотенуза, катет? Гіпотенуза – та, що стягує. Катет – перпендикуляр, відвіс. 10. Що піфагорійці називали «віслюковим мостом»?Теорему Піфагора. Вважали, що той, хто її не розуміє, «не пройде через неї» – справжній віслюк!