Презентація на тему:
Аксіоми геометрії

Аксіоми геометрії

АКСІОМИ ПЛАНІМЕТРІЇ

Аксіоми належності І1.. Яка б не була пряма, існують точки, що належать цій прямій, і точки, що не належать їй. І2.. Через будь-які дві точки можна провести пряму і до того ж тільки одну

Наслідки аксіом належності Дві різні прямі або не перетинаються, або перетинаються тільки в одній точці

Аксіоми розміщення ІІ1. З трьох точок на прямій одна і тільки одна лежить між двома іншими. ІІ2. Пряма розбиває площину на дві пів-площини

Наслідки аксіом розміщення Якщо кінці будь-якого відрізка належать одній півплощині, то відрізок не перетинає пряму. Якщо кінці відрізка належать різним півплощинам, то відрізок перетинає пряму

Аксіоми вимірювання ІІІ1. Кожний відрі має певну довжину, більшу від нуля. Довжина відрізка дорів-нює сумі довжин частин, на які він розбивається будь-якою його точкою. ІІІ2. Кожний кут має певну градусну міру, більшу від нуля. Розгорнутий кут дорівнює 180 . Градуснаміра кута дорівнює сумі градусних мір кутів, на які він роз-бивається будь-яким променем, що проходить між його сторонами

Наслідки аксіом вимірювання Якщо три точки А, В і С лежать на одній прямій, то точка С лежатиме між точками А і В у випадку, коли АВ = АС + СВ. Якщо від даної пів-прямої відкласти в одну й ту саму пів-площину два кути, то сторона меншого кута, відмінна від даної півпрямої, проходитиме між сторонами більшого кута

Аксіоми відкладання IV1. На будь-якій пів-прямій від її початкової точки можна відкласти відрізок заданої довжини і до того ж тільки один. IV2. Від будь-якої пів-прямої в задану пів-площину можна відкласти кут із заданою градусною мірою,меншою 180 , і до того ж тільки один. IV3. Який би не був трикутник, існує трикутник, що дорівнює йому, у заданому розміщенні відносно даної півпрямої

Наслідки аксіом відкладання Якщо пряма, яка не проходить через жодну з вершин трикутника, перетинає одну з його сторін, то вона перетинає тільки одну з двох інших сторін

Аксіома паралельності V1. Через точку, що не лежить на даній прямій, можна провести не більше як одну пряму, паралельну даній

Наслідки аксіоми паралельних Якщо пряма перетинає одну з двох паралельних прямих, то вона перетинає й другу

Аксіоми стереометрії і наслідки з них

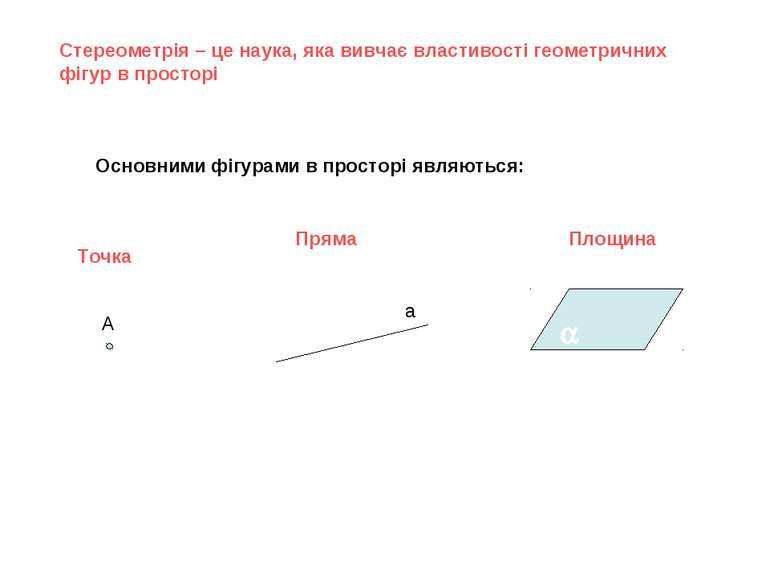
Стереометрія – це наука, яка вивчає властивості геометричних фігур в просторі Основними фігурами в просторі являються: Точка Пряма Площина A a

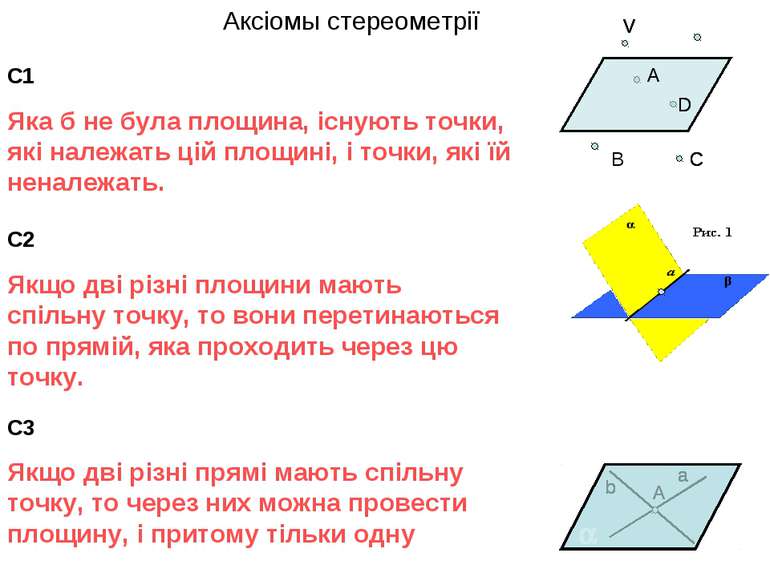
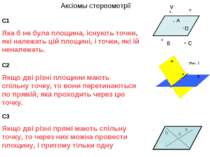
Аксіомы стереометрії С1 Яка б не була площина, існують точки, які належать цій площині, і точки, які їй неналежать. С2 Якщо дві різні площини мають спільну точку, то вони перетинаються по прямій, яка проходить через цю точку. С3 Якщо дві різні прямі мають спільну точку, то через них можна провести площину, і притому тільки одну V B C D A V V A V D A V D A V C D A V C A V D A b a A b a A b a A b a A b a A b a A b a A b a A b a

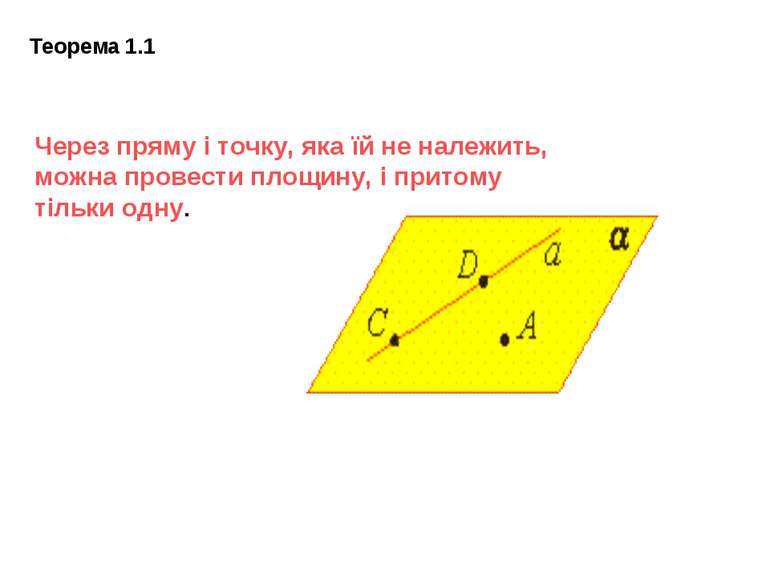
Теорема 1.1 Через пряму і точку, яка їй не належить, можна провести площину, і притому тільки одну.

Теорема 1.2 Якщо дві точки прямої належать площині, то вся пряма належить цій площині.

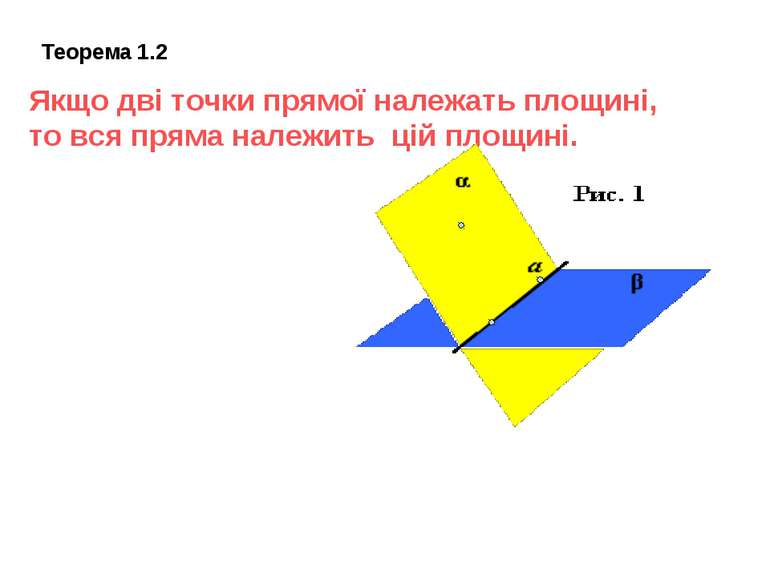
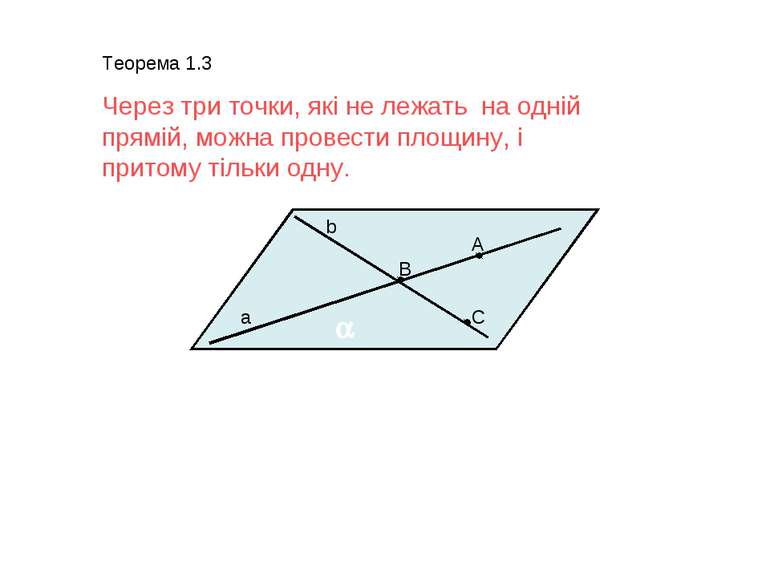
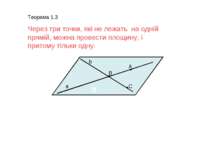
Теорема 1.3 Через три точки, які не лежать на одній прямій, можна провести площину, і притому тільки одну. A B C a b