Презентація на тему:
Історія геометрії

Видатні геометри

Фалес Мілетський (кінецьVII – початок VI ст. до н.е.) – грецький астроном і математик. За свідченням грецького історика Плутарха, Фалес вимірював висоту єгипетської піраміди за довжиною її тіні: довжину тіні піраміди відноситься до довжини тіні вертикального стовпа, поставленого поруч з пірамідою, як невідома висота піраміди відноситься до довжини цього стовпа. Теорему, яку тепер називають теоремою Фалеса, можливо, сам він і не знав. Жодне з його доведень до нас не дійшло.

Фалес Мілетський

Клавдій Птолемей (близько 87 — 165) —давньогрецький вчений,твори якого мали великий вплив на розвиток астрономії, географії та оптики. Дані про життя Птолемея мізерні. Жив у римській провінції Єгипет і працював в Александрії. Створив геоцентричну систему світу, розробив математичну теорію руху планет навколо нерухомої Землі, яка дозволяла обчислювати їхнє положення на небі. Система Птолемея викладена в його головній праці «Альмагест» — енциклопедії астрономічних знань давнини. У 1543 польський астроном Микола Копернік запропонував альтернативну, геліоцентричну систему. У праці Птолемея «Географія» були представлені географічні відомості античного світу, нею користувалися аж до 16 століття.

Клавдій Птолемей

Евклід( близько 365 — близько 300 до н. е.) Історія не зберегла для нас достовірних відомостей про життя цього видатного вченого. Вважають, що Евклід народився в Афінах близько 325 p. до н. е. і на запрошення царя Птолемея І на початку III ст. до н. е. прибув до Александрії. Працюючи в бібліотеці Музейону над упорядкуванням математичних манускриптів, Евклід створив славнозвісну працю з математики, яку назвав «Начала». «Начала» Евкліда складаються з 13 «книг»-сувоїв. Перші шість книг присвячені планіметрії, VII—X книги — арифметиці і несумірним величинам, які можна побудувати за допомогою циркуля і лінійки, XI— XIII — стереометрії. І книга починається викладом 23 означень і 10 аксіом, причому перші п'ять з цих аксіом називаються «загальними поняттями», а решта — «постулатами» (у різних списках «Начал» є різні кількості аксіом і постулатів). 

Евклід

Теореми

В геометрії, Теорема Фалеса (названа на честь Фалеса Мілетського) стверджує, що якщо A, B і C є точками на колі де відрізок AC є діаметром кола, тоді кут ABC є прямим.

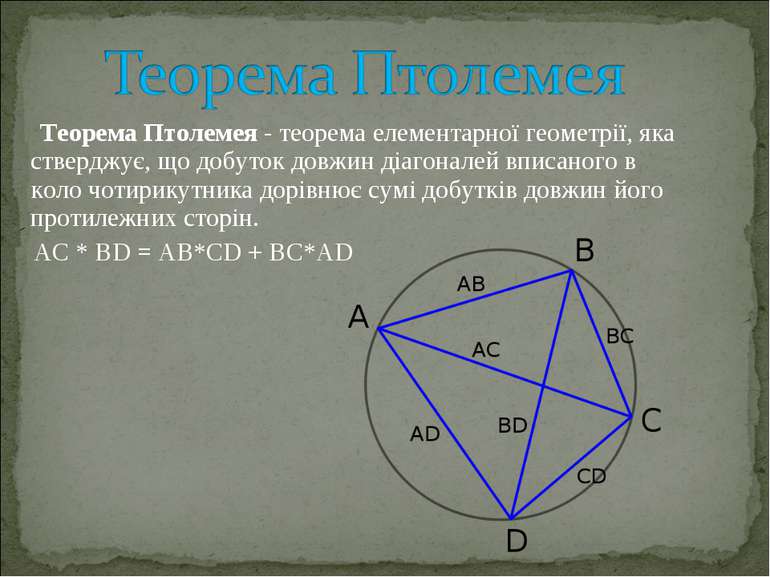
Теорема Птолемея - теорема елементарної геометрії, яка стверджує, що добуток довжин діагоналей вписаного в коло чотирикутника дорівнює сумі добутків довжин його протилежних сторін. AC * BD = AB*CD + BC*AD

Геометричні терміни

Трапеція (грец. Trapecion)-столик. Сам термін Trapecion склався від грецького ж слова trapesa, основним значенням якого є “стіл”. Колись трапезою називали їжу. Але з часом цей термін став означати загальний обідній стіл для ченців в монастирських приміщеннях. У геометрії розуміння трапеції як чотирикутника, в якого дві сторони паралельні, а дві інші непаралельні, склалося відразу. Так Евклід, визначивши поняття паралелограма, прямокутника, квадрата і ромба, всі останні чотирикутники назвав трапеціями.

Ромб(грец. Rombos)- дзиґа, бубон. Зрозуміло, що мається на увазі не сама дзиґа, а її силует. Можливо,що і бубон колись мав такий же силует. Що таке ромб як геометрична фігура, знали вже старогрецькі математики. Так в “Початках” Евкліда ми знаходимо означення:”З чотиристороніх фігур, ромб – рівностороння, але не прямокутна”. Як бачимо, за цим означенням ми не можемо квадрат розглядати як ромб.

Квадрат (лат. quadratus) – чотирикутний. В давнину люди, що мали справу з предметами форми чотирикутника(землеміри, будівельники і тому подібне), не зналися на тонкощах класифікації чотирикутників по їх видах. Поза сумнівом, що вони представляли квадрат, як чотирикутник від інших многокутників, є те, що він складається “з чотирьох сторін (кутів)”. На латинській мові вираження “з чотирьох” передається словами “ex quadre” (екс кварде). Звідси і виник тармін “quadratus”-”чотирикутний”.

Така вона – геометрія. З роками не старіє, а стає дедалі необхіднішою.