Презентація на тему:
Задачі з економіки, які розв’язуються за допомогою похідної

Група « Знавці» Працювали під девізом: « Усе, що я пізнаю, я знаю, для чого це мені потрібно, де і як я можу ці знання застосувати.» та вивчали Задачі з економіки, які розв’язуються за допомогою похідної

Задачі з економіки, які розв’язуються за допомогою похідної Найбільш характерні: визначення загальної вартості утримання різних видів транспорту; визначення продуктивності праці; визначення попиту товарів, зміну доходів при збільшенні ціни; визначення затрат підприємств залежно від об’єму продукції, яка випускається; знаходження оптимальних розмірів продукції з найбільшим ( найменшим ) об’ємом (площею)

ЗАДАЧА 1 Вартість ( за годину) утримання баржі складається з двох частин: вартості палива, яка пропорційна кубу швидкості баржі, і вартості амортизації баржі ( заробітна плата команди, обладнання та ін.). Загальна вартість утримання баржі за годину, таким чином, виразиться формулою , де v – швидкість судна в км/год; a і b – коефіцієнти, задані для кожного судна. Визначити, при якому v загальна сума утримання на 1 км шляху буде найменшою, якщо a = 0,005, b = 40.

Розв’язання Розв’язання За умовою a = 0,005, b = 40, тоді . 1 км шляху баржа пройде за год. За цей час витрати складуть , Треба знайти найменше значення функції на проміжку ; якщо; , ; ; v= 10 . Оскільки, безперервна на проміжку і v= 10 одна стаціонарна точка, то вона є точкою мінімуму, бо . V = 10 =10 · 1,6=16 ( км / год. ). Відповідь: 16 км/ год.

Задача 2 Об’єм продукції u, яку виробляє бригада робітників, описується рівнянням (од.), , де t – робочий час в годинах. Обчислити продуктивність праці , швидкість і темп її зміни через час після початку роботи і за час до її закінчення.

Розв’язання Продуктивність праці виражається похідною z (t) = u/ (t) = - ( од./год.), а швидкість і темп зміни продуктивності – відповідно похідною z/ (t) і похідною логарифмічної функції z/ (t) = -5t + 15 (од./год 2), ( од./год.) У задані моменти часу і відповідно маємо: z ( 1) = 112,5 (од/год), z/ (1) = 10 (од./год2 ), T ( 1)= 0,09 (од./год) і z(7) =82,5 (од./год.), z/ (7) = -20 (од./год2 ), T (7)= - 0,24 (од/год) Таким чином, до кінця роботи продуктивність праці суттєво знижується, при цьому зміна знаку z/ (t) і T( t ) з плюса на мінус свідчить про те, що збільшення продуктивності праці у першу годину робочого дня змінюється її пониженням в останню годину.

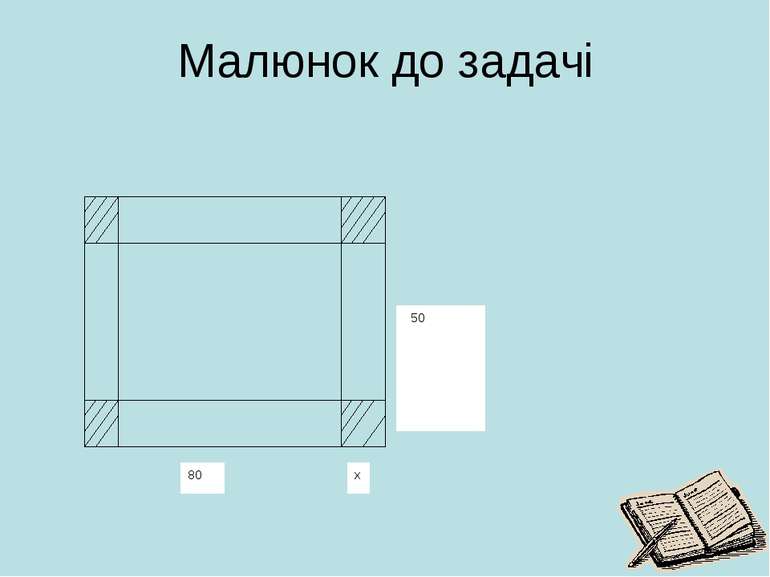
Задача 3 Дано прямокутний лист жерсті розміром 80 х 50 см. Треба виготовити з нього відкриту зверху коробку найбільшої місткості, вирізавши по кутах квадрати і загнувши краї. Якою повинна бути довжина сторони такого квадрата?

Малюнок до задачі

Розв’язання Позначимо через х довжину сторони квадрата, що вирізується. Очевидно, що 0 ≤х ≤25. Об’єм коробки ( прямокутного паралелепіпеда ) дорівнює добутку площі основи на висоту. При зазначеному способі виготовлення коробки основа її - прямокутник із сторонами 80 -2х і 50 – 2х, а висота х;. відповідно об’єм коробки становить: V (x )= ( 80-2x ) (50-2x) x = 4x3-260x2+ 4000x Задача звелась до знаходження найбільшого значення функції на проміжку [0; 25] Знайдемо критичні точки (x )= ( 4x3-260x2+ 4000x )/ =12х2-520х + 4000 12х2-520х + 4000=0; х = і х = 10. Інших критичних точок функція не має, бо похідна існує для всіх х. Проміжку [ 0;25] належить лише одна точка х=10. Обчислимо значення V (x ) у цій точці і на кінцях проміжку: V (10 ) = 4 ·103-260· 102+ 4000·10 =1800; V (0 ) = 0; V (25 ) = 4· 253-260 ·252+ 4000 ·25=0 Отже, найбільшого значення функція V (x ) досягає на проміжку [0; 25] у точці 10. Це означає, що коробку найбільшого об’єму можна виготовити, вирізавши по кутах даного листа жерсті квадрати із стороною 10 см.

До побачення!