Презентація на тему:
Відстань між двома точками. Координати середини відрізка

ВІДСТАНЬ МІЖ ДВОМА ТОЧКАМИ. КООРДИНАТИ СЕРЕДИНИ ВІДРІЗКА.

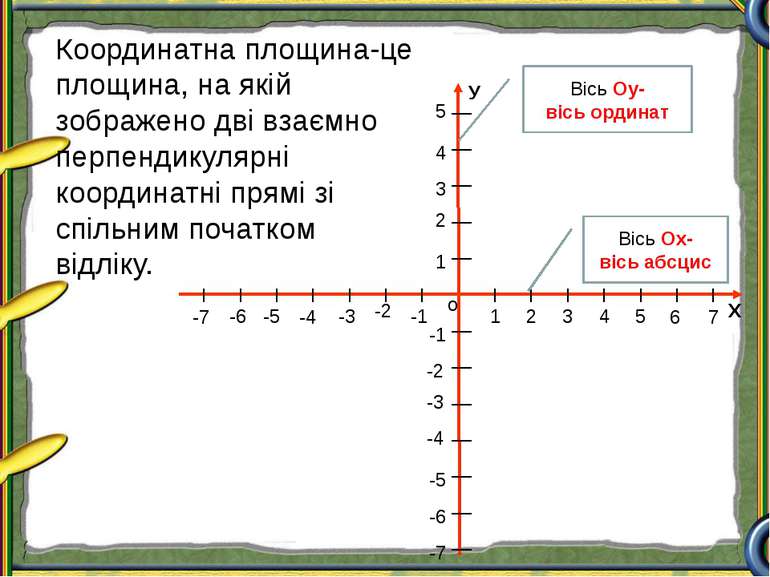
Х о У 1 2 3 4 5 1 2 3 4 5 -1 -2 -3 -4 -5 -1 -2 -4 -5 -6 -3 6 -7 7 -6 -7 Координатна площина-це площина, на якій зображено дві взаємно перпендикулярні координатні прямі зі спільним початком відліку. Вісь Оу- вісь ординат Вісь Ох- вісь абсцис

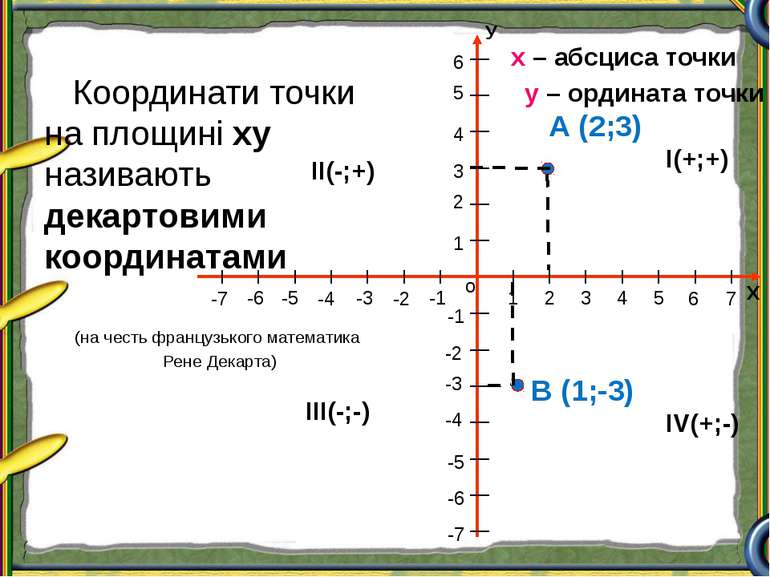
Координати точки на площині ху називають декартовими координатами (на честь французького математика Рене Декарта) А (2;3) В (1;-3) І(+;+) ІІ(-;+) ІІІ(-;-) ІV(+;-) х – абсциса точки у – ордината точки Х о У 1 2 3 4 5 1 2 3 4 5 -1 -2 -3 -4 -5 -1 -2 -4 -5 -6 -3 6 -7 7 6 -6 -7

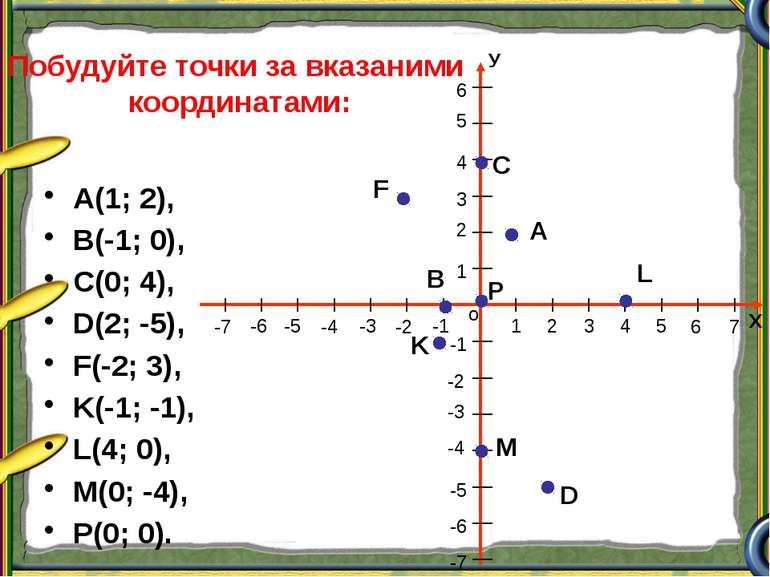
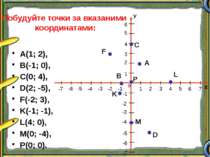
А(1; 2), В(-1; 0), С(0; 4), D(2; -5), F(-2; 3), K(-1; -1), L(4; 0), M(0; -4), P(0; 0). Побудуйте точки за вказаними координатами: А В С D F K L M P Х о У 1 2 3 4 5 1 2 3 4 5 -1 -2 -3 -4 -5 -1 -2 -4 -5 -6 -3 6 -7 7 6 -6 -7

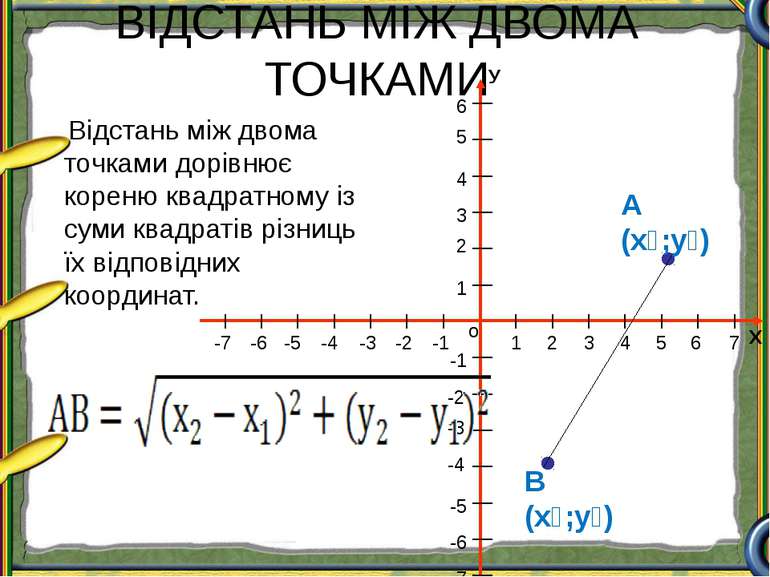
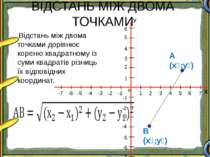
ВІДСТАНЬ МІЖ ДВОМА ТОЧКАМИ А (х₁;у₁) В (х₂;у₂) Відстань між двома точками дорівнює кореню квадратному із суми квадратів різниць їх відповідних координат. Х о У 1 2 3 4 5 1 2 3 4 5 -1 -2 -3 -4 -5 -1 -2 -4 -5 -6 -3 6 -7 7 6 -6 -7

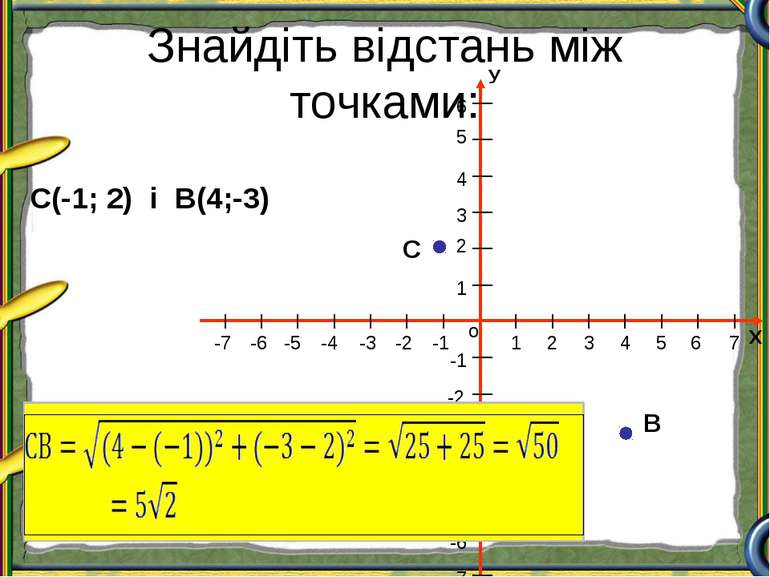
Знайдіть відстань між точками: С(-1; 2) і В(4;-3) С В Х о У 1 2 3 4 5 1 2 3 4 5 -1 -2 -3 -4 -5 -1 -2 -4 -5 -6 -3 6 -7 7 6 -6 -7

Вершинами трикутника є точки А(-1;3), В(5;9), С(6;2). Доведіть, що трикутник-рівнобедрений. ВС=АС, АВС- рівнобедрений.

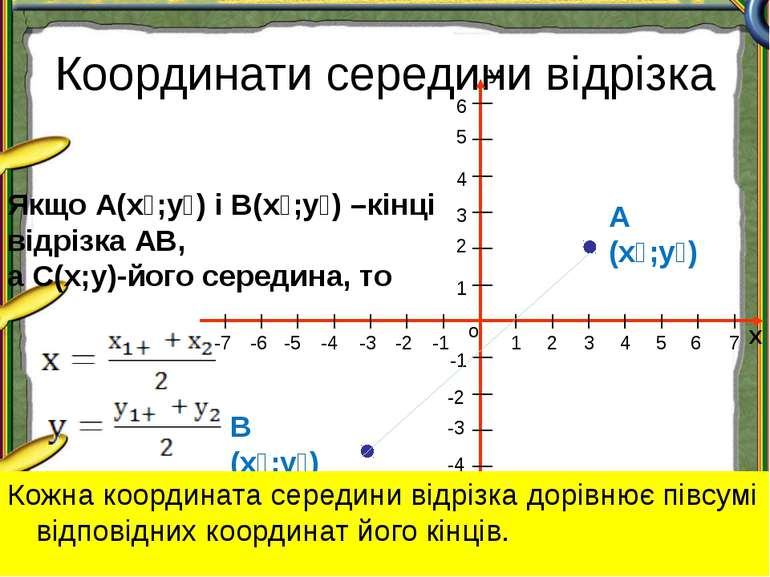
Координати середини відрізка А (х₁;у₁) В (х₂;у₂) Якщо А(х₁;у₁) і В(х₂;у₂) –кінці відрізка АВ, а С(х;у)-його середина, то , а Кожна координата середини відрізка дорівнює півсумі відповідних координат його кінців. Х о У 1 2 3 4 5 1 2 3 4 5 -1 -2 -3 -4 -5 -1 -2 -4 -5 -6 -3 6 -7 7 6 -6 -7

При якому значенні х відстань між точками С(3;-2) і Д(х;-1) дорівнює 5? х-3=4, х=7