Презентація на тему:
Степенева функція з цілим показником

Алгебра і початки аналізу. 10 клас (за підручником Мерзляк А. Г.)

Тема уроку: Степенева функція з цілим показником

Степенева функція з цілим показником Функцію, яку можна задати формулою y = xn, де n ∈ Z, називають степеневою функцією з цілим показником. Властивості цієї функції для натурального показника було розглянуто на попередньому уроці. Тепер розглянемо випадки, коли показник n є цілим від’ємним числом або нулем (y = x0, y = x-1, y = x-2). Областю визначення функції y = x0=1 є множина (–∞; 0) c (0; +∞), областю значень — одноелементна множина {1}. Графік цієї функції зображено на рисунку 73.

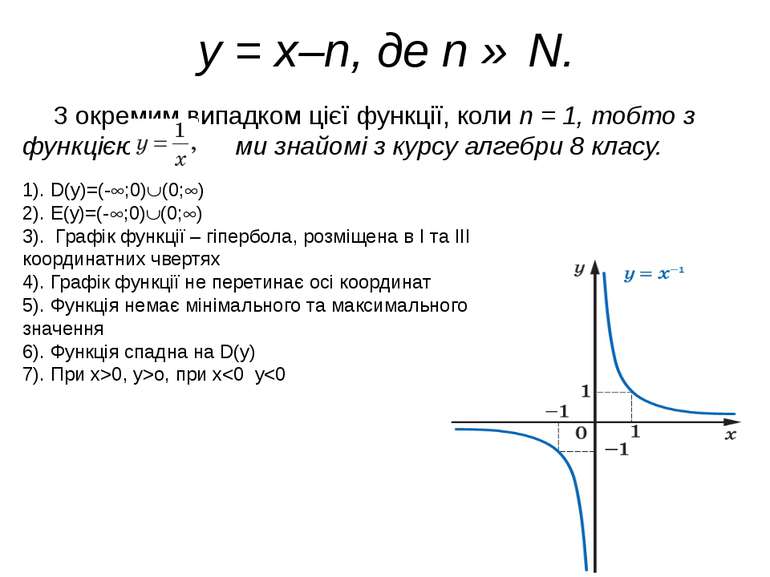
y = x–n, де n ∈ N. З окремим випадком цієї функції, коли n = 1, тобто з функцією ми знайомі з курсу алгебри 8 класу. 1). D(y)=(- ;0) (0; ) 2). E(y)=(- ;0) (0; ) 3). Графік функції – гіпербола, розміщена в І та ІІІ координатних чвертях 4). Графік функції не перетинає осі координат 5). Функція немає мінімального та максимального значення 6). Функція спадна на D(y) 7). При х>0, y>o, при х

Запишемо функцію y = x–n у вигляді Областю визначення функції y = x–n, n ∈ N, є множина (–∞; 0) (0; +∞). Очевидно, що ця функція нулів не має. Подальші дослідження властивостей функції y = x–n, де n ∈ N, проведемо для двох випадків: n — парне натуральне число n — непарне натуральне число.

n = 2k, k ∈ N Маємо: Оскільки вираз набуває тільки додатних значень, то до області значень розглядуваної функції не входять від’ємні числа, а також число 0. Для будь-якого a > 0 існує таке значення аргументу x, що x–2k = a.

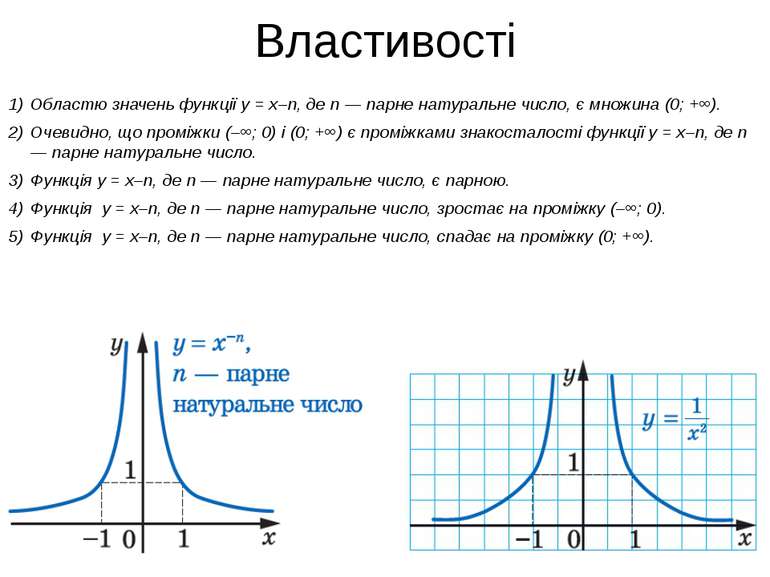
Властивості Областю значень функції y = x–n, де n — парне натуральне число, є множина (0; +∞). Очевидно, що проміжки (–∞; 0) і (0; +∞) є проміжками знакосталості функції y = x–n, де n — парне натуральне число. Функція y = x–n, де n — парне натуральне число, є парною. Функція y = x–n, де n — парне натуральне число, зростає на проміжку (–∞; 0). Функція y = x–n, де n — парне натуральне число, спадає на проміжку (0; +∞).

n = 2k – 1, k ∈ N Для будь-якого a ≠ 0 існує таке значення аргументу x, що x–(2k – 1) = a. Областю значень функції y = x–n, де n — непарне натуральне число, є множина (–∞; 0) (0; +∞). Проміжки (–∞; 0) і (0; +∞) є проміжками знакосталості функції y = x–n, де n — непарне натуральне число. Функція y = x–n, де n — непарне натуральне число, є непарною. Функція y = x–n, де n — непарне натуральне число, спадає на кожному з проміжків (–∞; 0) і (0; +∞).

Висновки

Первинне закріплення вивченого матеріалу Яку функцію називають степеневою функцією з цілим показником? Яка область визначення функції y = x0? Яка область значень функції y = x0? Яка фігура є графіком функції y = x0? Яка область визначення степеневої функції з цілим від’ємним показником? Сформулюйте властивості функції y = x–n, де n — парне натуральне число. Як виглядає графік функції y = x–n, де n — парне натуральне число? Сформулюйте властивості функції y = x–n, де n — непарне натуральне число. Як виглядає графік функції y = x–n, де n — непарне натуральне число?

Тренувальні вправи

Тренувальні вправи

Тренувальні вправи

Домашнє завдання Читати § 10 Готувати відповіді на контрольні запитання 1-9 ст. 95 Виконати вправи №№ 273, 275, 277, 279, 284, 286