Презентація на тему:
Похідна та її застосування

Ісаак Ньютон Готфрід Лейбніц

Архімед

Нікколо Тарталья Йоганн Кеплер Нікколо Тарталья Рене Декарт

«За даною довжиною шляху в будь-який момент часу зна й ти швидкість руху у вказаний час» Ісаак Ньютон

Швидкість зміни функції у точці називається похідною функції у точці

Таблиця похідних

Правила обчислення похідних

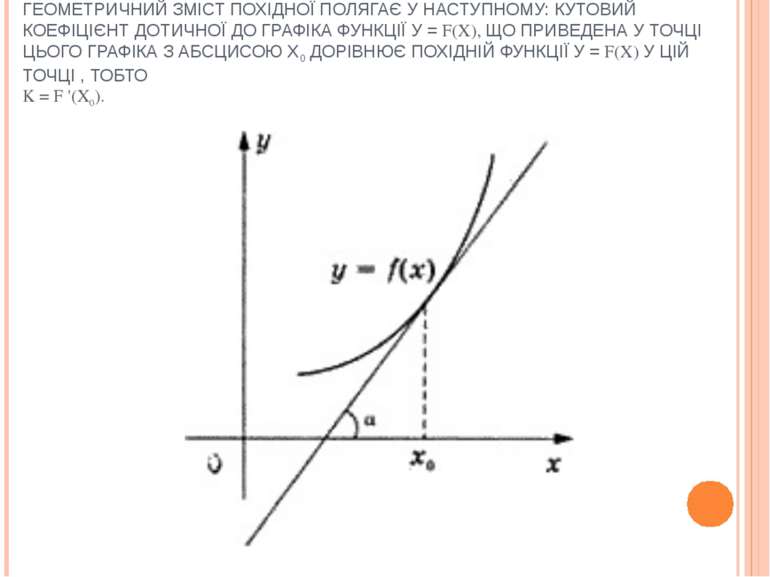
ГЕОМЕТРИЧНИЙ ЗМІСТ ПОХІДНОЇ ПОЛЯГАЄ У НАСТУПНОМУ: КУТОВИЙ КОЕФІЦІЄНТ ДОТИЧНОЇ ДО ГРАФІКА ФУНКЦІЇ У = F(X), ЩО ПРИВЕДЕНА У ТОЧЦІ ЦЬОГО ГРАФІКА З АБСЦИСОЮ Х0 ДОРІВНЮЄ ПОХІДНІЙ ФУНКЦІЇ У = F(X) У ЦІЙ ТОЧЦІ , ТОБТО K = F '(X0).

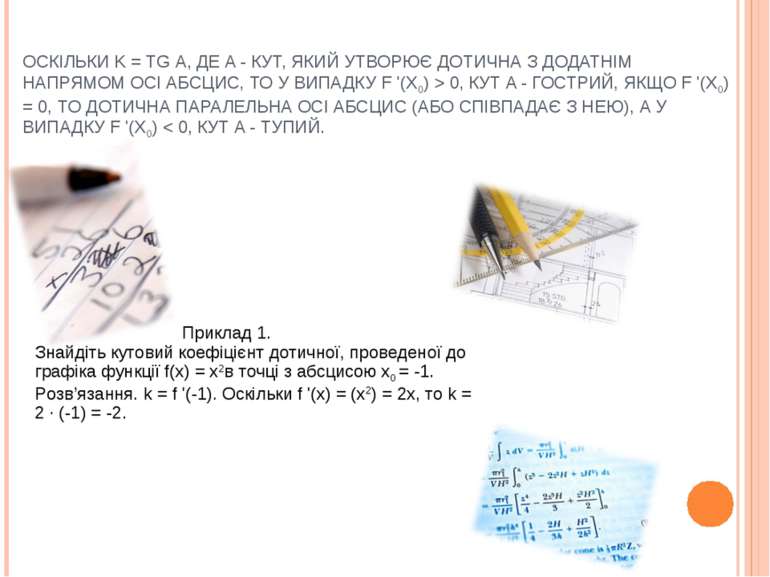
ОСКІЛЬКИ K = TG Α, ДЕ Α - КУТ, ЯКИЙ УТВОРЮЄ ДОТИЧНА З ДОДАТНІМ НАПРЯМОМ ОСІ АБСЦИС, ТО У ВИПАДКУ F '(X0) > 0, КУТ Α - ГОСТРИЙ, ЯКЩО F '(X0) = 0, ТО ДОТИЧНА ПАРАЛЕЛЬНА ОСІ АБСЦИС (АБО СПІВПАДАЄ З НЕЮ), А У ВИПАДКУ F '(X0) < 0, КУТ Α - ТУПИЙ. Приклад 1. Знайдіть кутовий коефіцієнт дотичної, проведеної до графіка функції f(х) = х2в точці з абсцисою х0 = -1. Розв’язання. k = f '(-1). Оскільки f '(x) = (х2) = 2х, то k = 2 ∙ (-1) = -2.

ПРИКЛАД 2. ЗНАЙДІТЬ КУТ НАХИЛУ ДО ОСІ АБСЦИС ДОТИЧНОЇ, ПРОВЕДЕНОЇ ДО ГРАФІКА ФУНКЦІЇ F(Х) = 2, ЩО ПРОВЕДЕНА В ТОЧЦІ А(1; 2). РОЗВ’ЯЗАННЯ.    ТОДІ   A ТОМУ Α = Π/4.

ПРИКЛАД 3. НА ГРАФІКУ ФУНКЦІЇ   ЗНАЙДІТЬ ТАКІ ТОЧКИ, В ЯКИХ ДОТИЧНА, ПРОВЕДЕНА ДО ГРАФІКА ФУНКЦІЇ, ПАРАЛЕЛЬНА ОСІ АБСЦИС. РОЗВ’ЯЗАННЯ. НЕХАЙ Х0 - АБСЦИСА ШУКАНОЇ ТОЧКИ. ТОДІ, ВИХОДЯЧИ З УМОВИ F(Х0) = 0, МАЄМО:  ЗНАХОДИМО X0 = 0 АБО Х0 = -2. ОТЖЕ, ВРАХОВУЮЧИ,   ТАКИМИ ТОЧКАМИ Є ТОЧКИ (0;0) І (2;-4).

РІВЕНЬ ДОТИЧНОЇ ДО ГРАФІКА ФУНКЦІЇ У = F(X), ЩО ПРОВЕДЕНА В ТОЧЦІ З АБСЦИСОЮ Х0, ЩО НАЛЕЖИТЬ ГРАФІКУ ФУНКЦІЙ, МАЄ ВИГЛЯД ПРИКЛАД 1. СКЛАДІТЬ РІВНЯННЯ ДОТИЧНОЇ ДО ГРАФІКА ФУНКЦІЇ F(X) = LN Х + Х2 В ТОЧЦІ З АБСЦИСОЮ Х0= 1. РОЗВ’ЯЗАННЯ.   ТОМУ РІВНЯННЯ ДОТИЧНОЇ МАЄ ВИГЛЯД: У = 1 + 3(Х - 1), АБО ПІСЛЯ СПРОЩЕННЯ У = 3Х - 2. ПРИКЛАД 2. СКЛАДІТЬ РІВНЯННЯ ДОТИЧНОЇ ДО ГРАФІКА ФУНКЦІЇ F(Х) = Х2 - 4Х + 7, ЯКА ПАРАЛЕЛЬНА ПРЯМІЙ У = 2Х. РОЗВ’ЯЗАННЯ. КУТОВИЙ КОЕФІЦІЄНТ ПРЯМОЇ У = 2Х ДОРІВНЮЄ 2. ТОМУ КУТОВИЙ КОЕФІЦІЄНТ ШУКАНОЇ ДОТИЧНОЇ ТАКОЖ МАЄ ДОРІВНЮВАТИ 2, ОСКІЛЬКИ ВОНА ПАРАЛЕЛЬНА ДО ПРЯМОЇ У = 2Х. ОТЖЕ, F‘(Х0) = 2, ДЕ Х0 - ШУКАНА ТОЧКА. МАЄМО F '(Х) = 2Х - 4. З РІВНЯННЯ 2Х - 4 = 2 МАЄМО Х0 = 3. ТОДІ F(3) = З2 - 4 ∙ 3 + 7 = 4. ШУКАНЕ РІВНЯННЯ ДОТИЧНОЇ: У = 4 + 2(Х - 3) АБО ПІСЛЯ СПРОЩЕНЬ У = 2Х - 2.

Похідна в фізиці і у техніці

РІЗНІ ЗАДАЧІ, ЩО ПОВ’ЯЗАНІ З ПОНЯТТЯМ ПОХІДНОЇ , ЗУСТРІЧАЛИСЯ У ПРАЦЯХ Н.ТАРТАЛЬЇ , Й.КЕПЛЕРА , Р.ДЕКАРТА ТА ІНШИХ . Рене Декарт Иоганн Кеплер Никколо Тарталья

І.НЬЮТОН СФОРМУЛЮВАВ І РОЗВ’ЯЗАВ ОСНОВНУ ПРОБЛЕМУ МАТЕМАТИЧНОГО АНАЛІЗУ : « ЗА ДАНОЮ ДОВЖИНОЮ ШЛЯХУ В БУДЬ-ЯКИЙ МОМЕНТ ЧАСУ ЗНАЙТИ ШВИДКІСТЬ РУХУ У ВКАЗАНИЙ ЧАС » . І ЯКЩО ВІН ВИХОДИВ ІЗ ЗАДАЧ МЕХАНІКИ , ТО Г.ЛЕЙБНІЦ - ІЗ ГЕОМЕТРИЧНИХ ЗАДАЧ . Г.ЛЕЙБНІЦА ПЕРВІСНИМ ПОНЯТТЯМ ДЛЯ ПОХІДНОЇ БУЛА ДОТИЧНА , А У І.НЬЮТОНА – ШВИДКІСТЬ . Исаак Ньютон Готфрид Вильгельм Лейбниц

РОЗВ'ЯЗАННЯ : v(t )= x/∆ t де х- це координата переміщення матеріальної точки (тіла), ∆ t- проміжку часу, за який це переміщення відбувалось, тобто, функція швидкості руху v(t) є похідною від функції х(t). В момент часу t=4с швидкість дорівнює v =2*4-3=5м/с.

ПРИСКОРЕННЯ ШВИДКОСТІ РУХУ МАТЕРІАЛЬНОЇ ТОЧКИ А (T) Є ПОХІДНОЮ ВІД ФУНКЦІЇ ШВИДКОСТІ V(T). ОСКІЛЬКИ ФУНКЦІЯ ШВИДКОСТІ РУХУ V(T) Є ПОХІДНОЮ ВІД ФУНКЦІЇ Х(T), ТО ФУНКЦІЯ ПРИСКОРЕННЯ ШВИДКОСТІ РУХУ МАТЕРІАЛЬНОЇ ТОЧКИ Є ДРУГОЮ ПОХІДНІЮ ФУНКЦІЇ Х(T), АБО ПОХІДНОЮ ДРУГОГО ПОРЯДКУ. А (T) = V’(T) =(Х’(T))’ В даному випадку прискорення стале для довільного значення t, тобто точка рухається рівноприскорено.

Застосування похідної до дослідження функції

ЗАСТОСУВАННЯ ПОХІДНОЇ ДО ДОСЛІДЖЕННЯ ФУНКЦІЇ

ПИТАННЯ: Яка функція називається зростаючою? Яка функція називається спадною? Що називається точкою мінімуму? Що називається точкою максимуму? Які точки називаються критичними?

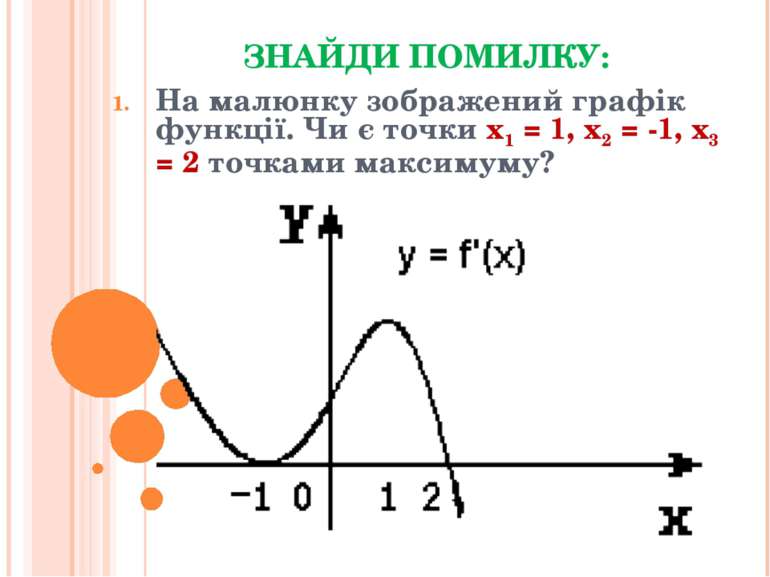
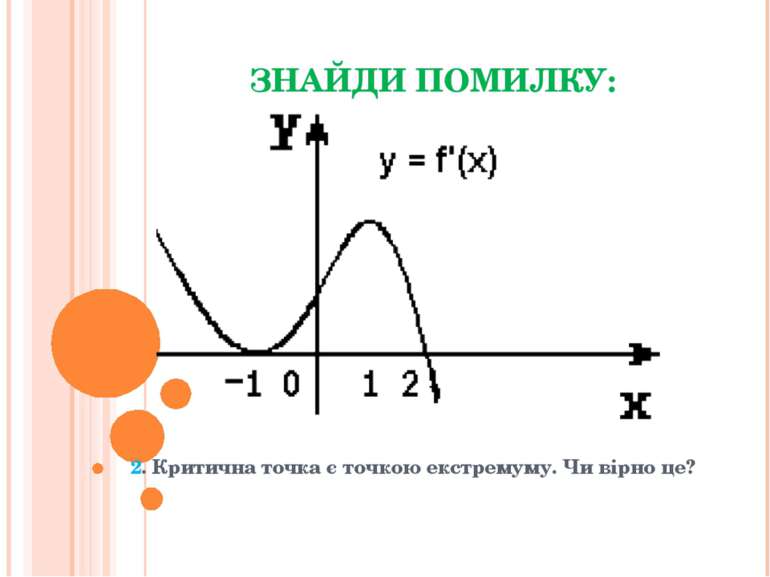
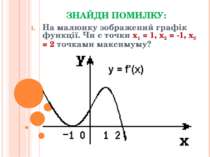
ЗНАЙДИ ПОМИЛКУ: На малюнку зображений графік функції. Чи є точки x1 = 1, x2 = -1, x3 = 2 точками максимуму?

ЗНАЙДИ ПОМИЛКУ: 2. Критична точка є точкою екстремуму. Чи вірно це?

ІСТОРИЧНІ ФАКТИ Саме він в 1797 році ввів поняття похідна, що являється буквальним перекладом французького слова “deviree”. Цей вчений ввів сучасне позначення похідної функції: y’ та f ’.

ІСТОРИЧНІ ФАКТИ Один з творців (разом з І.Ньютоном) інтегрального та диференційного числення. В 1675 році довів обернений характер диференційного та інтегрального числення.

ЗАДАЧА ДІДОНИ

ПРАКТИЧНА РОБОТА: Для функції f(x) знайдіть: Область визначення. Похідну. Проміжки монотонності та екстремуми. По результам дослідження побудуйте графіки функцій. Дослідити функцію і побудувати графік f(x)=3х-x3

ЧИ ЗНАЄТЕ ВИ, ЩО … перша жінка-математик С. В. Ковалевська сказала: «Математик  повинен бути поетом в душі». Підберіть до графіків функцій, зображених на слайдах, прислів’я, які розкривають сутність процесів функції.

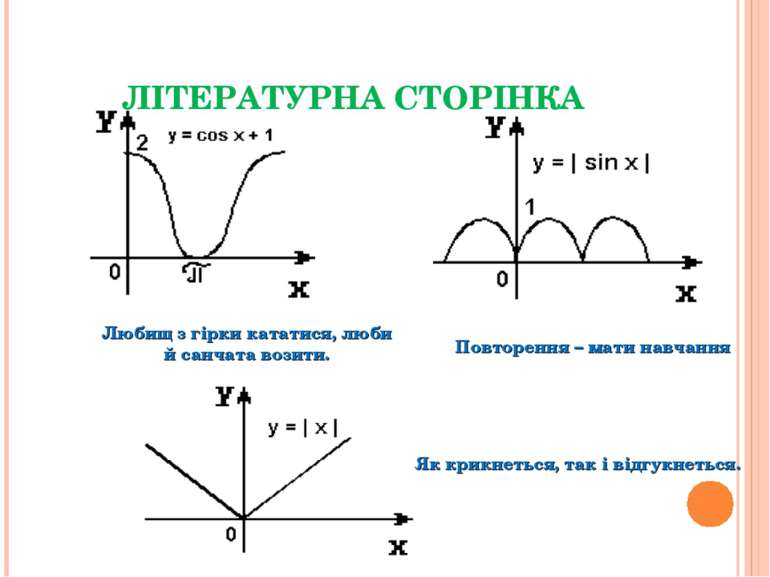
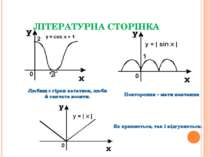
ЛІТЕРАТУРНА СТОРІНКА Любищ з гірки кататися, люби й санчата возити. Повторення – мати навчання Як крикнеться, так і відгукнеться.

ЗАДАЧА НА ЗНАХОДЖЕННЯ НАЙБІЛЬШОГО (НАЙМЕНШОГО) ЗНАЧЕНЬ ФУНКЦІЇ Число 64 записати у вигляді суми двох додатних доданків, щоб сума їх квадратівбула найменшою.

РОЗВ`ЯЗАННЯ Нехай один доданок буде х, тоді другий --- 64-х. 0

ВІДПОВІДЬ: 32 і 32

Оцінюємо роботу учнів , які розв'язували завдання на дошці , а також тих , хто брав участь у повторенні теоретичного матеріалу Урок завершується читанням учнями власних віршів про похідну