Презентація на тему:
Методика застосування похідної

Алгебра і початки аналізу.11 клас. Застосування похідної. (Матеріали для самостійного вивчення теми).

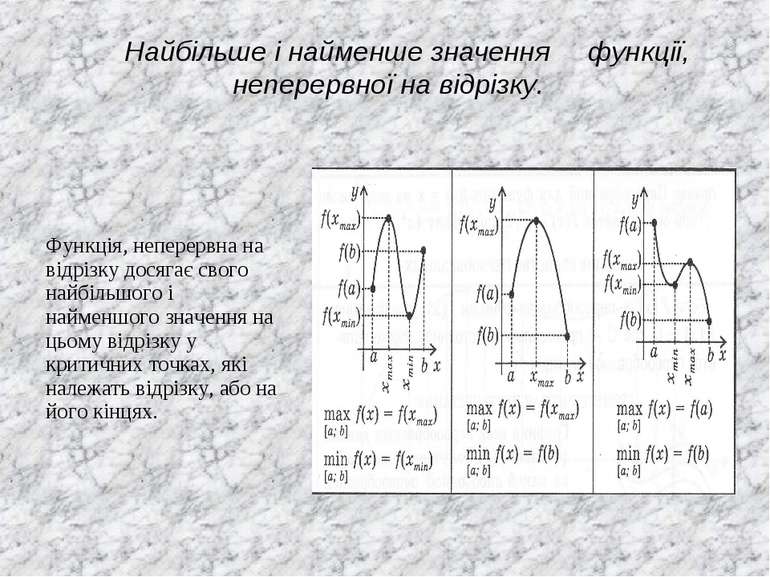
Зростання та спадання функції. Екстремальні точки. Локальний екстремум функції. Найбільше і найменше значення функції на проміжку Загальна схема дослідження функції для побудови графіків.

Алгоритм вивчення теми. Ознайомся і вивчи означення та теореми з даної теми, користуючись підручником та опорним конспектом Розглянь розв’язування типових вправ Виконай тренувальний тест Застосуй набуті знання й навички до виконання тренувальних вправ Виконай домашнє завдання

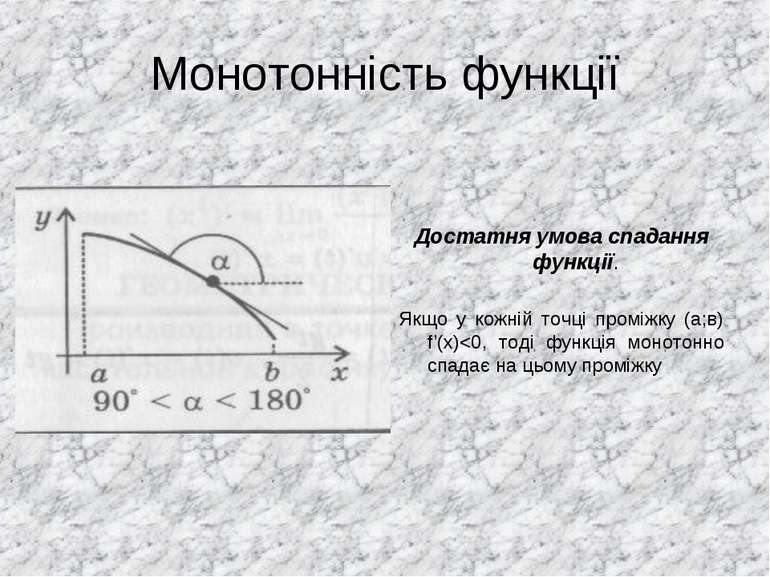
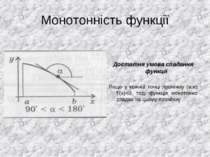
Монотонність функції Достатня умова спадання функції. Якщо у кожній точці проміжку (а;в) f’(x)

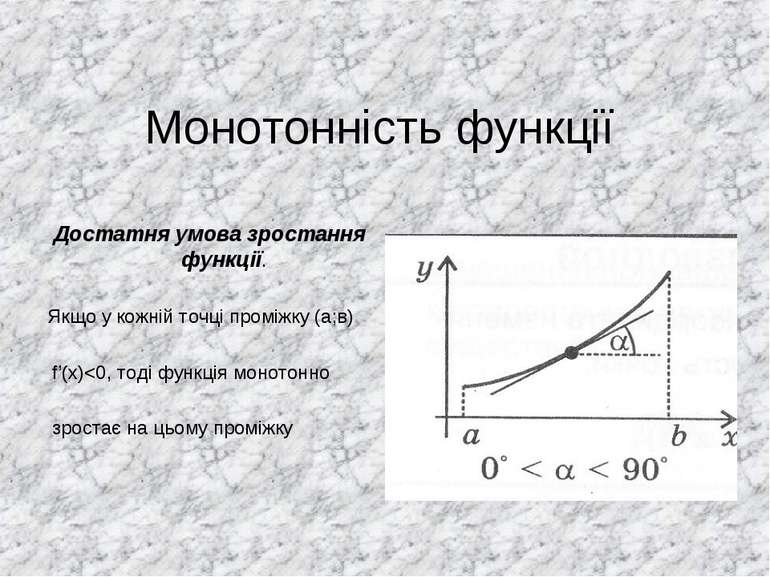
Монотонність функції Достатня умова зростання функції. Якщо у кожній точці проміжку (а;в) f’(x)

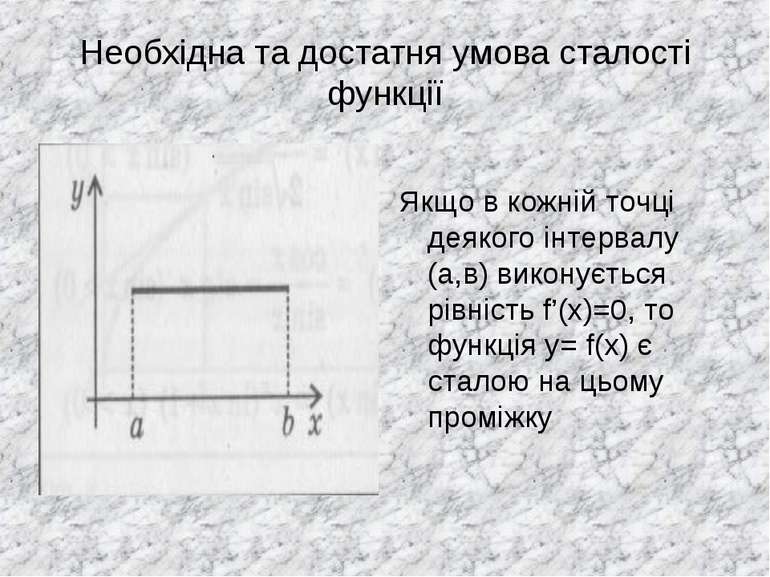
Необхідна та достатня умова сталості функції Якщо в кожній точці деякого інтервалу (а,в) виконується рівність f’(x)=0, то функція у= f(x) є сталою на цьому проміжку

Екстремуми функцій

Приклади екстремумів

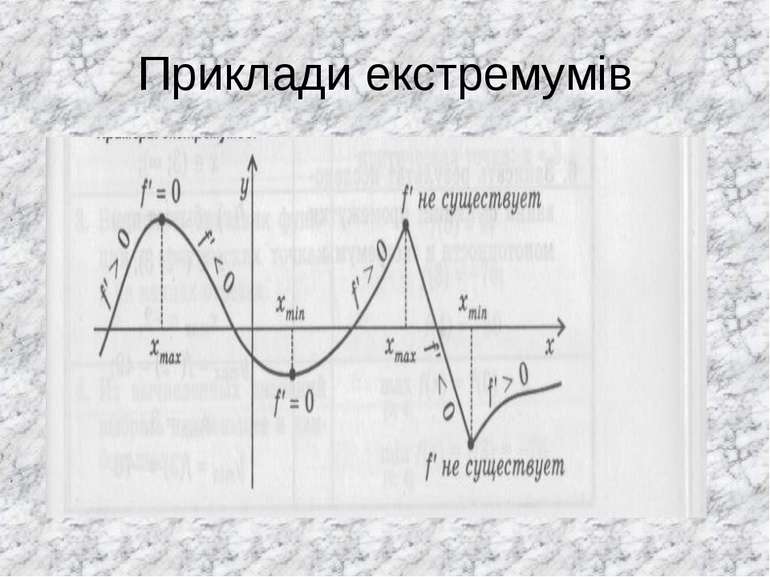
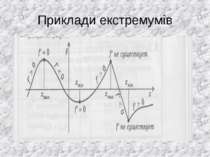
Алгоритм застосування похідної для знаходження інтервалів зростання та спадання функції та ії екстремумів -2 3 + - + f’ f x

Найбільше і найменше значення функції, неперервної на відрізку.

Алгоритм знаходження найбільшого і найменшого значень функції, неперервної на відрізку

Схема повного дослідження функції 1.*Знайти Д( у). *Дослідити на парність. *Дослідити на періодичність. *Знайти нулі функції та точки перетину графіка з віссю ОУ. 2.*Знайти F’(x). *Знайти критичні точки. *Знайти проміжки монотонності та точки екстремуму. 3. *Знайти F’’(x). *Розв”язати рівняння F’’(x) = 0. *Знайти точки перегину та проміжки випуклості і вогнутості. 4. *Знайти асимптоти: вертикальні та похилі (горизонтальні як частковий випадок) . 5.*При потребі обчислити координати контрольних точок. 6. *Побудувати графік функції. 7. *Знайти Е(у).

Розв’язування типових вправ

Зразок оформлення розв’язання завдання на дослідження функції на монотонність. у= 4х3+6х2 -8 Розв’язування. D(у)=R у'=12х2+12х=12х(х+1) 12х(х+1)›0, якщо х(х+1)›0 12х(х+1)‹0, якщо х(х+1) ‹0 Розв’яжемо кожне з нерівностей методом інтервалів g(х)= х(х+1); D(g)=R нулі функції: g(х)=0, х(х+1)=0; х1=0; х2=-1 g(х) ›0, якщо х Є (-∞;-1) та х Є (0;+∞) g(х) ‹ 0, якщо х Є (-1; 0) Маємо: функція у= 4х3+6х2 -8 – зростає, якщо х Є (-∞;-1) та х Є (0;+∞), спадає, якщо х Є (-1; 0) Відповідь: (-1; 0) – інтервал спадання функції (-∞;-1) U (0;+∞) - інтервал зростання функції.

2. Зразок оформлення розв’язання вправи на знаходження найбільшого та найменшого значення функції на проміжку. Знайдіть найбільше і найменше значення функції f (х) = х3 – 3х2 – 45х + 2 на проміжку [-5; 7] Розв’язання: f’ (х) = 3х2 – 6х – 45 f’ (х) існує для всіх х є R, тоді критичних точок немає, а стаціонарні точки найдемо за умови f’ (х) = 0, тоді 3х2 – 6х – 45 х2 – 2х – 15 = 0 х1 = -3; х2 = 5 -3 Є [-5; 7]; 5 Є [-5; 7] f(-5) = (-5)3 – 3 · (-5)2 – 45 · (-5) + 2 = 27 f (-3) = (-3)3 – 3 · (-3)2 – 45 · (-3) + 2 = 83 f (5) = 53 – 3 · 52 – 45 · 5 + 2 = - 173 f (7) = 73 – 3 · 72 – 45 · 7 + 2 = - 117 - 173 < - 117 < 27 < 83 min f (х) = f (5) = - 173 max f (х) = f (-3) = 83 [-5; 7] [-5; 7]

Зразок оформлення розв’язання вправи на знаходження екстремумів

4. Дослідити функцію і побудувати графік функції

Зразок розв’язання задачі на находження найбільшого та найменшого значення

Тренувальні тести

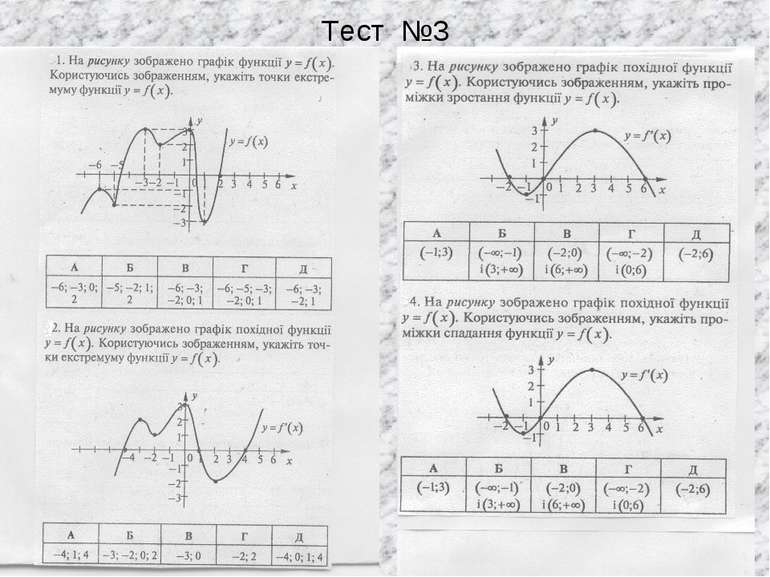
Тест №1. Знайдіть проміжки зростання функції а) у= 3х2-12х +8 1) (-∞;-2) 2) (-2;+∞) 3) (-∞;2) 4) (2;+∞), б) у= х3-3х (-1;1) 2) (-∞;-1) і (1;+∞) 3) (-∞;-1) 4) (1;+∞), в) у= ех – х 1) (-1;+ ∞) 2) (-∞;1) 3) (0;+∞) 4) (-∞;0)

Тест №2. Знайдіть проміжки спадання функції а) у= х3-х (-1;1) 2) (-∞;-1) і (1;+∞) 3) (-∞;-1) 4) (1;+∞), б) у= 10х2-420х +151 1)(21;+ ∞) 2) (-∞;21) 3) (-21;+∞) 4) (-∞;-21)

Тест №3

Тест №4

Домашнє завдання 1. Вивчити § 15, §16, §17, §18, §19. 2. Відповісти на запитання стор. 96, стор.102 стор. 110. 3. Виконати вправи: №47(9, 11, 12), №48 (10, 13, 16) № 50 (3, 6, 9) №52 (5, 12)