Презентація на тему:
Метод інтервалів

Алгебра і початки аналізу. 10 клас (за підручником Мерзляк А. Г.)

Тема уроку: Метод інтервалів (2 уроки)

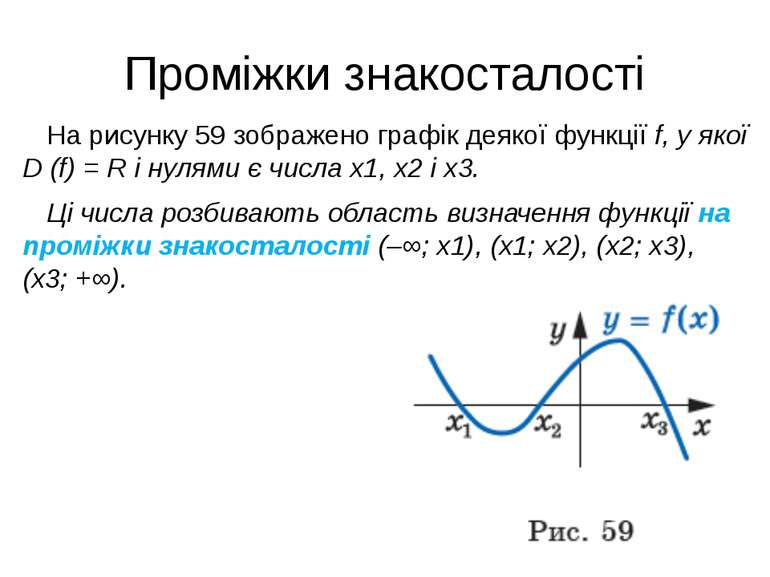
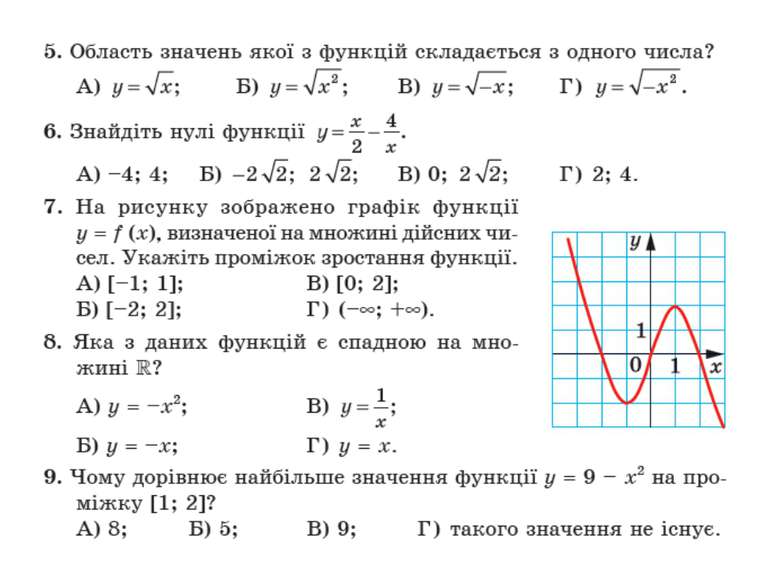
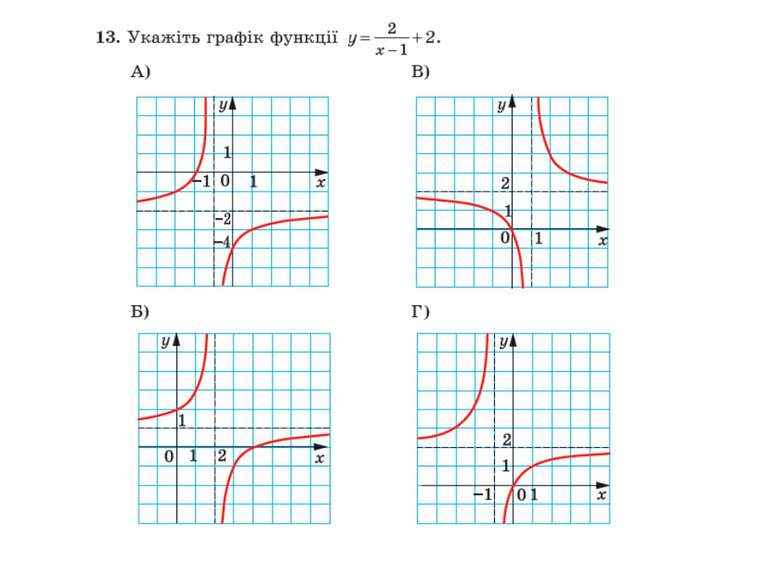
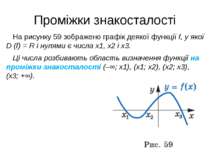
Проміжки знакосталості На рисунку 59 зображено графік деякої функції f, у якої D (f) = R і нулями є числа x1, x2 і x3. Ці числа розбивають область визначення функції на проміжки знакосталості (–∞; x1), (x1; x2), (x2; x3), (x3; +∞).

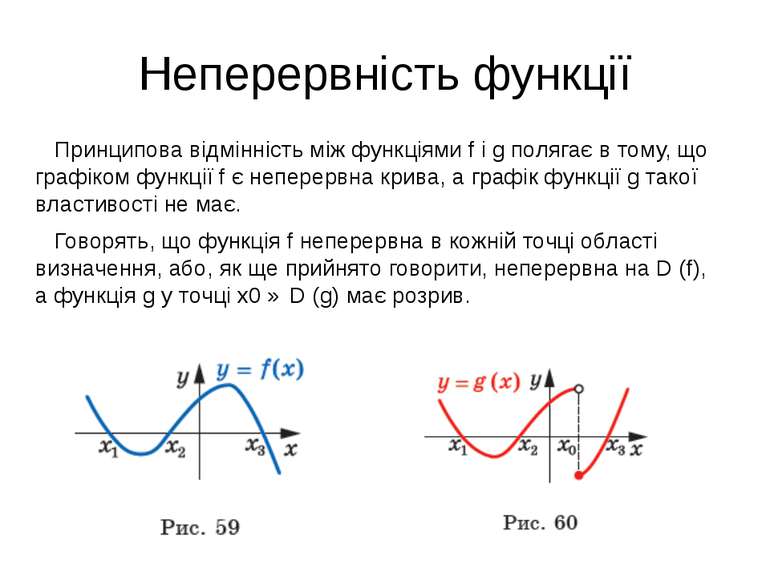
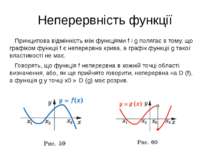
Проміжки знакосталості Для функції g, графік якої зображено на рисунку 60, проміжок (x2; x3) не є проміжком знакосталості. Справді, якщо x ∈ (x2; x0), то g (x) > 0, а якщо x ∈ (x0; x3), то g (x) < 0.

Неперервність функції Принципова відмінність між функціями f і g полягає в тому, що графіком функції f є неперервна крива, а графік функції g такої властивості не має. Говорять, що функція f неперервна в кожній точці області визначення, або, як ще прийнято говорити, неперервна на D (f), а функція g у точці x0 ∈ D (g) має розрив.

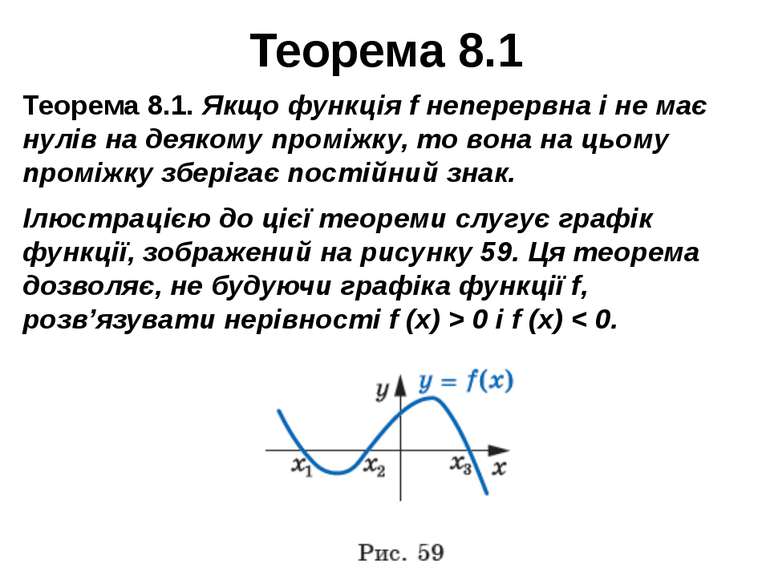
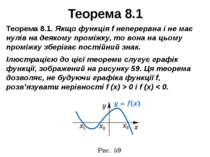
Теорема 8.1 Теорема 8.1. Якщо функція f неперервна і не має нулів на деякому проміжку, то вона на цьому проміжку зберігає постійний знак. Ілюстрацією до цієї теореми слугує графік функції, зображений на рисунку 59. Ця теорема дозволяє, не будуючи графіка функції f, розв’язувати нерівності f (x) > 0 і f (x) < 0.

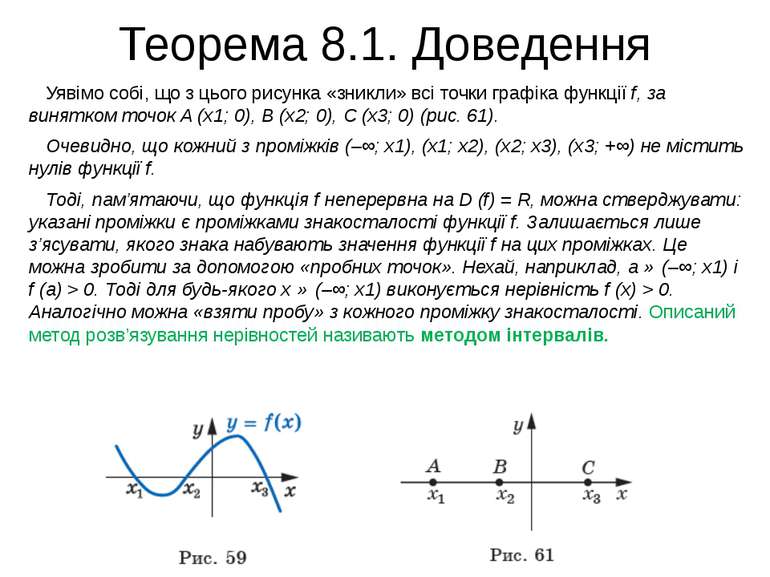
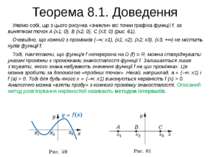
Теорема 8.1. Доведення Уявімо собі, що з цього рисунка «зникли» всі точки графіка функції f, за винятком точок A (x1; 0), B (x2; 0), C (x3; 0) (рис. 61). Очевидно, що кожний з проміжків (–∞; x1), (x1; x2), (x2; x3), (x3; +∞) не містить нулів функції f. Тоді, пам’ятаючи, що функція f неперервна на D (f) = R, можна стверджувати: указані проміжки є проміжками знакосталості функції f. Залишається лише з’ясувати, якого знака набувають значення функції f на цих проміжках. Це можна зробити за допомогою «пробних точок». Нехай, наприклад, a ∈ (–∞; x1) і f (a) > 0. Тоді для будь-якого x ∈ (–∞; x1) виконується нерівність f (x) > 0. Аналогічно можна «взяти пробу» з кожного проміжку знакосталості. Описаний метод розв’язування нерівностей називають методом інтервалів.

Неперервність функції

Приклад 1 Розв’яжіть нерівність (x + 3) (x – 1) (x – 2) > 0.

Первинне закріплення вивченого матеріалу Чи завжди нулі функції розбивають її область визначення на проміжки знакосталості? Чи кожна неперервна функція зберігає постійний знак на про- міжку з області визначення, який не містить її нулів? Опишіть метод інтервалів розв’язування нерівностей.

Коментоване розв'язування вправ

Коментоване розв'язування вправ

Робота в групах

Кометроване розв'язування нерівностей

Робота в парах, коментарі вчителя та учнів, складання алгоритму розв'язування

Самостійна робота (робота за зразком)

Тренувальні вправи

Розв'язування нерівностей з параметрами

Узагальнююче повторення теми При вивченні матеріалу параграфа «Повторення та розширення відомостей про функцію» ви повторили, що: функція — це правило, за допомогою якого за кожним значенням незалежної змінної з множини X можна знайти єдине значення залежної змінної з множини Y. Незалежну змінну ще називають аргументом функції. Множину значень, яких набуває аргумент функції y = f (x), називають областю визначення функції і позначають D (f) або D (y). Множину значень, яких набуває залежна змінна, називають областю значень функції і позначають E (f) або E (y). Коли D (f) ⊂ R і E (f) ⊂ R, функцію f називають числовою; графіком числової функції f називають геометричну фігуру, яка складається з усіх тих і тільки тих точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати — відповідним значенням функції f; значення аргументу, при якому значення функції дорівнює нулю, називають нулем функції; проміжок, на якому функція набуває значень однакового знака, називають проміжком знакосталості функції; Функцію f називають зростаючою на множині M ⊂ D (f), якщо для будь-яких двох значень аргументу x1 і x2, які належать множині M, таких, що x1 < x2, виконується нерівність f (x1) < f (x2); Функцію f називають спадною на множині M ⊂ D (f), якщо для будь-яких двох значень аргументу x1 і x2, які належать множині M, таких, що x1 < x2, виконується нерівність f (x1) > f (x2); якщо функція зростає на всій області визначення, то її називають зростаючою. Якщо функція спадає на всій області визначення, то її називають спадною; графік функції y = f (x) + b можна отримати в результаті паралельного перенесення графіка функції y = f (x) на b одиниць угору, якщо b > 0, і на –b одиниць униз, якщо b < 0; графік функції y = f (x + a) можна отримати в результаті паралельного перенесення графіка функції y = f (x) на a одиниць уліво, якщо a > 0, і на –a одиниць управо, якщо a < 0; графік функції y = kf (x) можна отримати, замінивши кожну точку графіка функції y = f (x) на точку з тією самою абсцисою і ординатою, помноженою на k; Рівняння f1 (x) = g1 (x) і f2 (x) = g2 (x) називають рівносильними, якщо множини їх коренів рівні; нерівності називають рівносильними, якщо множини їх розв’язків рівні.

Узагальнююче повторення теми Ви дізналися, що: якщо для всіх x ∈ M виконується нерівність f (x0) m f (x), де x0 ∈ M, то число f (x0) називають найменшим значенням функції f на множині M і записують якщо для всіх x ∈ M виконується нерівність f (x0) l f (x), де x0 ∈ M, то число f (x0) називають найбільшим значенням функції f на множині M і записують функцію f називають парною, якщо для будь-якого x з області визначення f (–x) = f (x); функцію f називають непарною, якщо для будь-якого x з області визначення f (–x) = –f (x); вісь ординат є віссю симетрії графіка парної функції; початок координат є центром симетрії графіка непарної функції; графік функції y = f (kx), де k > 0, можна отримати, замінивши кожну точку графіка функції y = f (x) на точку з тією самою ординатою і абсцисою, поділеною на k; функцію y = f (x) називають оборотною, якщо для будь-якого y0 ∈ E (f) існує єдине x0 ∈ D (f) таке, що y0 = f (x0); якщо функція є зростаючою (спадною), то вона є оборотною; Функції f і g називають взаємно оберненими, якщо: 1) D (f) = E (g) і E (f) = D (g); 2) для будь-якого x0 ∈ D (f) з рівності f (x0) = y0 випливає, що g (y0) = x0, тобто g (f (x0)) = x0; графіки взаємно обернених функцій симетричні відносно прямої y = x; якщо функція f є зростаючою (спадною), то обернена функція g є також зростаючою (спадною); якщо множина коренів рівняння f2 (x) = g2 (x) містить множину коренів рівняння f1 (x) = g1 (x), то рівняння f2 (x) = g2 (x) називають наслідком рівняння f1 (x) = g1 (x); якщо множина розв’язків першої нерівності є підмножиною множини розв’язків другої нерівності, то другу нерівність називають наслідком першої нерівності.

Домашнє завдання Читати §§ 1-8 Готуватися до тематичної контрольної роботи Виконати №№ 215, 217, 219, 221, 224, 227 (завдання самостійно розподілити на 2 уроки)