Презентація на тему:
Формування опорних конспектів з алгебри

Автори Антонова Світлана В'ячеславівна Вчитель математики спеціаліст вищої категорії Павлик Катерина Володимирівна Вчитель математики спеціаліст вищої категорії, старший вчитель Черкаської загальноосвітньої школи І – ІІІ ступенів №32

Анотація Основною метою використання ОК є: навчання учнів аналізувати теоретичний матеріал і виділяти основне; полегшити вивчення означень і тверджень. Робота за ОК спирається на наочність, полегшує первинне сприйняття учнями матеріалу, запам'ятовування опорної інформації та її повторення , привчає виділяти головне, висловлюватись лаконічно та математично обґрунтовано, полегшує формування логічного ланцюжка доведення та блок-схеми розв'язання, тобто сприяє формуванню алгоритмічного мислення. Усне промовляння ОК за його схемою вчить учнів математичному мовленню. Використання ОК у навчанні школярів полегшує формування в них не лише наочно-образного та алгоритмічного мислення, але й мовної культури.

Зміст Рівняння Цілі вирази Функції Системи лінійних рівнянь з двома змінними

Рівняння Загальні відомості про рівняння Основні властивості рівнянь Лінійні рівняння з однією змінною Розв'язування задач за допомогою рівнянь

Загальні відомості про рівняння Рівняння - рівність , яка містить змінні (невідомі числа, позначені буквами). 2х – 13 = 2,5 Корінь (розв’язок) рівняння – число, яке задовольняє рівняння. Розв’язати рівняння : знайти всі його корені або показати, що їх не існує.

Основні властивості рівнянь 1. У будь-якій частині рівняння можна розкрити дужки і звести подібні доданки рівняння. 2. Будь-який член рівняння можна перенести з однієї частини рівняння в іншу змінивши його знак на протилежний 4х + 34 = 16х – 7 ; 4х – 16х = - 7 - 34 3. Обидві частини рівняння можна помножити або поділити на одне й те саме число відмінне від 0 х + 5 = 0,5 3х – 27 = 63 10х + 50 = 5 х – 9 = 21

Лінійні рівняння Рівняння вигляду ах = b, у якому а і b – деякі числа ( коефіцієнти ), х – змінна називається лінійним рівнянням з одним невідомим ах = b а ≠ 0 b ≠ 0 х = b : а Один корінь а = 0 b ≠ 0 0· х = b немає коренів а = 0 b = 0 0· х = 0 безліч коренів

Розв'язати лінійне рівняння 2(х + 3) - 3(х - 2) = 2х + 6 1. Розкрити дужки 2. Перенести члени зі змінною в ліву частину рівняння, а інші – в праву. 3. Звести подібні доданки 4. Поділити обидві частини рівняння на коефіцієнт при змінній 1. 2х + 6 – 3х + 6 = 2х + 6 2. 2х – 3х – 2х = = - 6 – 6 + 6 3. -3х = - 6 4. х = 2

Розв'язування задач за допомогою рівнянь У двох цистернах зберігається 66т бензину, причому в першій бензину в 2 рази більше, ніж у другій. Скільки бензину в кожній цистерні ? 1. Вибрати невідоме і позначити його буквою 2. Використовуючи умову задачі, скласти рівняння 3. Розв'язати рівняння і дати відповіді на поставлені в задачі запитання 1.1 ц. -? т., в 2 р. б. 2х т 2 ц. -? т. х т. 2. Рівняння 2х + х = 66 3. 3х = 66 х = 22 22 т. – у другій цистерні , тоді в першій : 2 · 22 =44( т.) Відповідь : 44 т, 22 т. 66 т

Цілі вирази Вирази зі змінними Тотожні вирази Вирази зі степенями Одночлени Многочлени. Дії над многочленами Формули скороченого множення Розкладання многочленів на множники

Вирази зі змінними Раціональний вираз – вираз який містить додавання віднімання, множення , ділення, піднесення до степеня . Раціональний вираз, який не містить ділення на вираз зі змінною є цілим виразом. Числовий вираз утворюють із чисел, знаків дії, дужок. 25 + 34 – 7 : 2 Знайти значення числового виразу – виконати дії. Вираз не має змісту, якщо при знаходженні його значення приходять до дії , яку не можна виконати ( ділення на 0) Вираз зі змінними утворюють із букв, чисел, знаків дії і дужок. 4х -25; х² -4 Знайти значення виразу зі змінними – підставити замість букв певні значення і знайти значення числового виразу. При різних значеннях змінної різні значення виразу. а = 4х-3 при х = 2; а = 4·2 – 3 = 5; при х = 0; а = 4·0 – 3 = -3

Порядок виконання дій Дії : першого ступеня : додавання , віднімання другого ступеня : множення, ділення третього ступеня : піднесення до степеня У виразі без дужок : дії одного ступеня виконують у тому порядку, в якому вони записані. дії різних ступенів виконують спочатку дії вищого ступеня, а потім нижчого. У виразі з дужками спочатку виконують дії в дужках.

Тотожні вирази -вирази, які мають однакові числові значення, при всіх допустимих значеннях букв, що входять в них. Два тотожно рівні вирази сполучені знаком рівності - тотожності 2( а + с ) = 2а + 2с Заміна одного виразу іншим виразом , що тотожно дорівнює йому – є тотожним перетворенням виразів. Тотожні перетворення виразів ( спрощення виразів ) Розкриття дужок зведення подібних доданків 2(а + 3) – (а + 4) – (7а - 3) = = 2а + 6 – а – 4 – 7а + 3 = - 6а + 5

Вирази зі степенями Степенем числа а з натуральним показником n називають добуток n множників , кожний з яких дорівнює а аⁿ : а – основа степеня ; n – показник степеня. аⁿ = а · а · а · а ··· а n разів 0ⁿ = 0; а1= а а > 0, n - довільне : an > 0 а < 0, n - парне : an > 0 n – непарне : an < 0 Властивості степеня : a n · a m = a n + m a n : a m = a n – m ,n > m ( a n ) m = a n ·m ( a · b ) n =a n · b n

Одночлен – добуток чисел змінних та їх степенів. 4а3с2р ; 4х ; 2,3 ; ас ; у Стандартний вигляд одночлена – одночлен який містить тільки один числовий множник( коефіцієнт ), який стоїть на першому місці, і степені різних букв. 2а5с4х; 7ху; 23а2х Коефіцієнт – числовий множник одночлена, записаного в стандартному вигляді 2а5с4х; 7ху; 23а2х Степінь одночлена – число, яке дорівнює сумі показників степені, які входять в цей одночлен 3х3у2а1, k = 3+ 2+1 = 6 Подібні одночлени – одночлени, які відрізняються тільки коефіцієнтами х2у ; 0,7 х2у ; -15 х2у Добуток одночленів є одночлен -3а2с · 4ас3 = -3 · 4 · а2 · а · с · с3 = -12а3с4 Щоб піднести одночлен до степеня необхідно кожний множник піднести до цього степеня (-2ар2) 5 = -32 · а5 · р10

Многочлен – сума одночленів. Члени многочлена – одночлени, з яких складається многочлен. 144 – аb2 – двочлен a b – 2c2 + d3 – тричлен Подібні члени многочлена – подібні одночлени, які входять в цей многочлен. Звести подібні члени многочлена – виконати дії над подібними одночленами . 3ах - 7с + 2ах + 3с = 3ах + 2ах + ( -7с + 3с) = 5ах - 4с Многочлен стандартного вигляду – многочлен, який не має подібних членів . х4 -2х3 +7ах + 7 - стандартного вигляду Степінь многочлена стандартного вигляду – найбільший степінь одночлена, що входить в цей многочлен а5 – 3а2т + 2ах + 7 ; k = 5 5 2+1 1+1 0

Дії над многочленами Додавання і віднімання многочленів. Перетворити у многочлен стандартного вигляду (2а + 3х – 4с) – (-5а + 4х + с ) 1.Розкрити дужки 2а + 3х – 4с + 5а - 4х - с 2.Звести подібні доданки 7а – х – 5с Множення многочлена на одночлен ( а + b – d) · c = a · c + b · c - d · c Множення многочлена на многочлен ( a + b ) · ( c + d ) = a · c + a · d + b · c + b · d

Формули скороченого множення Різниця різниці суму квадратів виразів виразів a2 – b2 = ( a – b ) · ( a + b ) Квадрат квадрат подвоєний квадрат двочлена першого добуток другого ( a + b ) 2 = a2 + 2ab + b2 ( a - b ) 2 = a2 - 2ab + b2 Різниця і сума або неповний квадрат сума кубів різниця різниці або суми a3 ± b 3 = ( a ± b) · ( a2 a · b + b2)

Розкладання многочленів на множники - подання многочлена у вигляді добутку кількох многочленів або одночлена на многочлен. Винесення спільного множника за дужки a · b + a · c = a · ( b + c ) Спосіб групування Подати многочлен у вигляді добутку m · k – m · n + x · k – x · n = 1.Згрупувати члени даного многочлена на вирази, що мають спільний множник = (m· k – m· n) + (x· k – x· n)= 2.Винести за дужки спільний множник ( одночлен ) = m· (k – n) + x· (k – n) = 3.Винести за дужки спільний множник (многочлен) = (k – n)· (m + x)

Використання формул скороченого множення для розкладання многочленів на множники a2 – b2 =(a - b) · (a + b) a2 +2ab +b2 =(a+b)2 a2 -2ab +b2 =(a-b)2 a3+b3=(a+b)·(a2-a·b+b2) a3-b3=(a-b)·(a2+a·b+b2) 25a2-b2=(5a-b)(5a+b) 16a2+8ab+b2=(4a+b)2 64x2-16xy+y2=(8x-y)2 27-x3=(3-x)(9+3x+x2) у3+8 =(y+2)(y2-2y+4)

Функції Означення функції. Способи задання функції. Графік функції. Лінійна функція.

ФУНКЦІЯ – залежність, при якій кожному значенню однієї змінної х (незалежної) відповідає єдине значення іншої (залежної) у. х – незалежна змінна аргумент, у – залежна змінна - функція у залежить від х : у(х) Приклади : площа круга від радіуса S ( R ) ; шлях пройдений зі сталою швидкістю від часу s ( t ) Область визначення функції – усі значення , які може набувати незалежна змінна ( значення х ) Область значень функції – усі значення залежної змінної (значення у)

Способи задання функцій 1. Аналітичний : за допомогою формули ( у = 2х3 – 5 ) 2. Графічний :зображають графіком функції у = f(х) в системі координат (див. далі) 3. Табличний : відповідність між елементами задається у формі таблиці 4. Словесним описом : закон відповідно якого значення функції відповідають значенням аргументу, формулюють словесно. ( розмір прибуткового податку є функцією заробітної плати платника)

Графік функції – множина всіх точок координатної площини, абсциси яких дорівнюють значенням аргументу, а ординати – відповідним значенням функції. Побудуємо графік функції, задану формулою у = х(3 – х), де -1 ≤ х ≤ 4 Складемо таблицю деяких відповідних значень аргументу й функції : Позначимо на координатній площині точки, координати яких подано у таблиці Функція набуває додатних значень (вище осі ОХ) при 0 < х < 3 ; від'ємних значень (нижче осі ОХ) при х < 0 та x > 3; Значення функції дорівнює нулю при х = 0, х = 3 у х 0 3 х -1 0 1 2 3 4 у -4 0 2 2 0 -4

Лінійна функція – функція, яку можна задати формулою виду у = k x + b,де х – незалежна змінна, k і b – деякі числа. Область визначення – усі числа. Графік функції - пряма. у = k x + b, 1. k > 0,b ≠ 0 2. k< 0,b ≠ 0 3. k ≠ 0,b = 0 4. k = 0,b – довільне число у 0 x k>0 k

Побудова графіка лінійної функції у = - х + 2 Щоб побудувати графік лінійної функції досить : 1. знайти координати двох точок графіка; 2. позначити ці точки в координатній площині; 3. провести через них пряму. 1. При x = 1, у = 1 при х = -2, у = 4 х 0 у 1 4 1 -2 у = - х +2

Системи лінійних рівнянь з двома змінними Рівняння з двома змінними. Графік лінійного рівняння з двома змінними. Система двох лінійних рівнянь. Розв'язування систем лінійних рівнянь: Графічний спосіб. Спосіб підстановки. Спосіб додавання. Розв'язування задач за допомогою систем лінійних рівнянь.

Рівняння з двома змінними – рівняння виду ах + bу = с, де х та у – змінні, а, b і с – числа ( коефіцієнти рівняння ) 5х – 7у = 34 Розв'язком рівняння із двома змінними називається пара значень невідомих, при яких рівняння перетворюється у правильну числову рівність. х + у = 8 х=4, у=4; х=4,5, у=3,5; х=10,у=-2 або (4;4) ; (4,5;3,5) ; (10;-2) Рівносильні рівняння з двома змінними – рівняння які мають одні й ті самі розв'язки або не мають розв'язків. Властивості рівнянь з двома змінними такі ж , як і рівнянь з одним невідомим

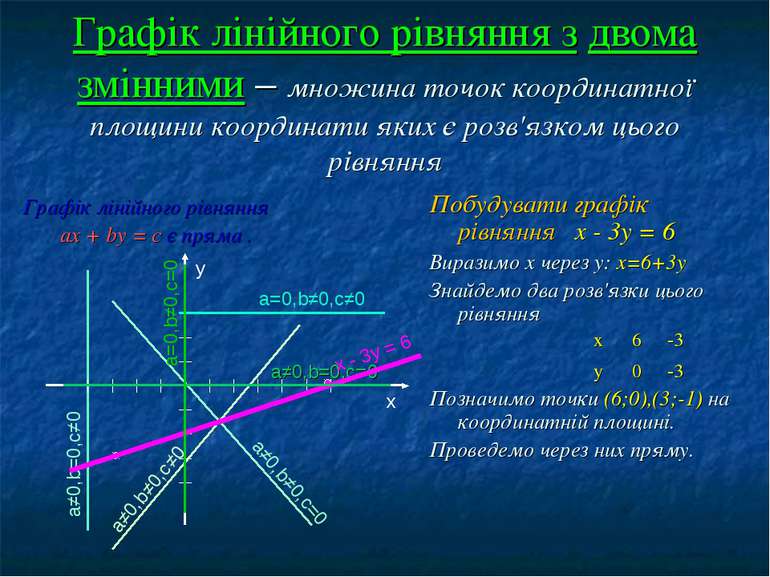
Графік лінійного рівняння з двома змінними – множина точок координатної площини координати яких є розв'язком цього рівняння Графік лінійного рівняння ах + bу = с є пряма . Побудувати графік рівняння х - 3у = 6 Виразимо х через у: х=6+3у Знайдемо два розв'язки цього рівняння Позначимо точки (6;0),(3;-1) на координатній площині. Проведемо через них пряму. a≠0,b≠0,c≠0 a≠0,b≠0,c=0 a=0,b≠0,c≠0 a≠0,b=0,c≠0 a=0,b≠0,c=0 a≠0,b=0,c=0 y x x - 3y = 6 х 6 -3 у 0 -3

Системи лінійних рівнянь із двома змінними Систему рівнянь утворюють два чи кілька рівнянь, якщо треба знайти їх спільні розв'язки. Систему рівнянь записують х + у = 56 за допомогою фігурної дужки. х - у = 4 Розв'язком системи рівнянь із двома невідомими називається пара значень невідомих ( х;у) , при яких кожне рівняння системи перетворюється у правильну числову рівність. Розв'язати систему рівнянь означає знайти всі її розв'язки або довести, що розв'язків немає.

Розв'язування систем лінійних рівнянь . Графічний спосіб Щоб розв'язати систему лінійних рівнянь графічним способом потрібно: 1. Побудувати графіки обох рівнянь в одній системі координат 2. Знайти координати спільних точок цих графіків. Розв'язати графічно систему рівнянь 5х-2у=11 х-3у=-3 5х - 2у =11 х - 3у =-3 х у 3 2 0 1 Відповідь : х=3,у=2 Х 1 3 у -3 2 Х 0 -3 у 1 0

Спосіб підстановки. Розв'язати систему рівнянь способом підстановки 2х + у = 12 7х - 2у = 31 1.Виражаємо з якого-небудь рівняння одну змінну через іншу. 2.Підставляємо у друге рівняння системи замість цієї змінної знайдений вираз. 3. Розв'язуємо утворене рівняння з однією змінною. 4. Знаходимо відповідне значення другої змінної. 1. у = 12 – 2х 2. 7х-2(12-2х)=31 3. 7х+4х-24=31 11х=55 ; х=5 4. у=-2·5+12=2 Відповідь : х=5,у=2

Спосіб додавання. Розв'язати систему рівнянь способом додавання 9у -5х = 23 4у – 2х = 6 1.Множимо почленно рівняння системи, підбираючи множники так, щоб коефіцієнти при одній зі змінних стали протилежними числами. 2. Додаємо почленно ліві й праві частини рівнянь системи. 3. Розв'язуємо утворене рівняння з однією змінною. 4. Підставляємо знайдене значення змінної в одне з даних рівнянь і знаходимо відповідне значення другої змінної. 1. 9у-5х=23 · 2 4у-2х=6 ·(-5) 2. 18у - 10х = 46 - 20у + 10х = - 30 -2у + 0 = 16 3. y = -8 4. 4 · (-8) - 2х = 6 -32 - 2х = 6 -2х = 38 х = -19 Відповідь : х = -19;у = -8

Розв'язування задач за допомогою систем рівнянь Сума двох чисел дорівнює 104. Одне з них на 11 більше від другого. Знайти ці числа. 1.Позначити деякі дві невідомі величини буквами. 2.Використовуючи умову задачі, скласти два рівняння. 3. Записати систему цих рівнянь і розв'язати її. 4. Дати відповіді на поставлені в задачі запитання. 1. 1 ч. - ? х 2 ч. - ? у 2. х + у =104 х – у =11 3. х + у =104 х – у =11 2х = 115 х = 57,5 - 1 число 57,5 – у = 11 у = 46,5 – 2 число 4. Відповідь : 1 число 57,5; 2 число 46,5 104 на 11