Презентація на тему:
Доведення нерівностей

Тема 2 Розв’язування лінійних нерівностей і систем нерівностей з однією змінною Лінійна нерівність з однією змінною. Рівносильні нерівності Система (та сукупність) нерівностей з однією змінною Числові проміжки. Переріз і об'єднання проміжків Нерівності, що містять модуль Розв’язування вправ. Самостійна робота Розв’язування систем ( та сукупностей) лінійних нерівностей з однією змінною. Доведення нерівностей Розв’язування вправ. Самостійна робота Розв'язування вправ

Готуємося до уроку Використано матеріали Бібліотеки електронних наочностей “Алгебра 7-9 клас”. Робота вчителя СЗОШ І- ІІІ ступенів № 8 м. Хмельницького Кравчук Г.Т. Мультимедійні технології на уроках алгебри 2011 рік

Пункт 2.4. Доведення нерівностей на основі означення понять “більше” і ”менше”. Приклади Інші способи доведення. Приклади Доведення нерівностей

Пригадайте 1). У чому достатньо пересвідчитись, щоб стверджувати, що а) m>n б) m

Пункт 2.4. Щоб довести цим способом, що A>B, досить утворити різницю лівої і правої частин нерівності і показати, що вона додатна (A-B>0). Аналогічно, щоб довести, що A

Пункт 2.4. Доведення. Покажемо, що різниця a2+b2-2ab – невід'ємне число. a2+b2-2ab=a2 -2ab+b2=(a-b)2≥0, бо квадрат будь-якого дійсного числа є невід'ємним числом. Отже, a2+b2≥2ab. Приклад 1. Довести, що при будь-яких значеннях a і b нерівність a2+b2≥2ab - правильна

Пункт 2.4. Доведення. Покажемо, що різниця a(a-2)-6(a-3)>0. Перетворимо вираз a(a-2)-6(a-3)=a2-2a-6a+18= =a2-8a+18. Виділимо з тричлена a2-8a+18 квадрат двочлена. a2-8a+18= a2-2а·4+42-42+18= =(а-4)2-16+18=(а-4)2+2. (а-4)2≥0 при будь-якому а, тому (а-4)2+2≥0. Оскільки a(a-2)-6(a-3)=(а-4)2+2 >0, то a(a-2)>6(a-3). Приклад 2. Довести, що a(a-2)>6(a-3)

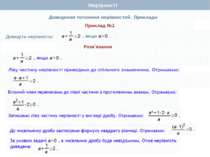
Пункт 2.4. Інші способи доведення Приклад4. Довести, що, якщо a, b, c – невід'ємні числа. Доведення. На основі встановленої нерівності, можемо стверджувати, що Додамо почленно ці нерівності. Маємо: або Поділимо обидві частини нерівності на 2, отримаємо:

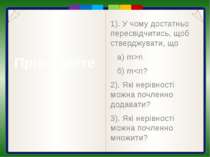
Пункт 2.4. Доведення. Помножимо почленно записані нерівності. Маємо: Враховуючи умову, що a, b, c – невід'ємні числа, можемо записати: Отже, (a+b)(b+c)(a+c)≥8abc Приклад 5. Довести, що (a+b)(b+c)(a+c)≥8abc, якщо a, b, c – невід'ємні числа

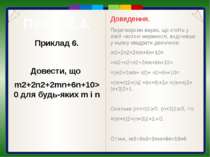
Пункт 2.4. Доведення. Перетворимо вираз, що стоїть у лівій частині нерівності, виділивши у ньому квадрати двочленів: m2+2n2+2mn+6n+10= =m2+n2+n2+2mn+6n+10= =(m2+2mb+ n2)+ n2+6n+10= =(m+n)2+(n2 +6n+9)+1= =(m+n)2+(n+3)2+1. Оскільки (m+n)2≥0, (n+3)2≥0, то =(m+n)2+(n+3)2+1>0. Отже, m2+2n2+2mn+6n+10>0 Приклад 6. Довести, що m2+2n2+2mn+6n+10>0 для будь-яких m і n

Тренувальні вправи