Презентація на тему:
Почленне додавання і множення нерівностей

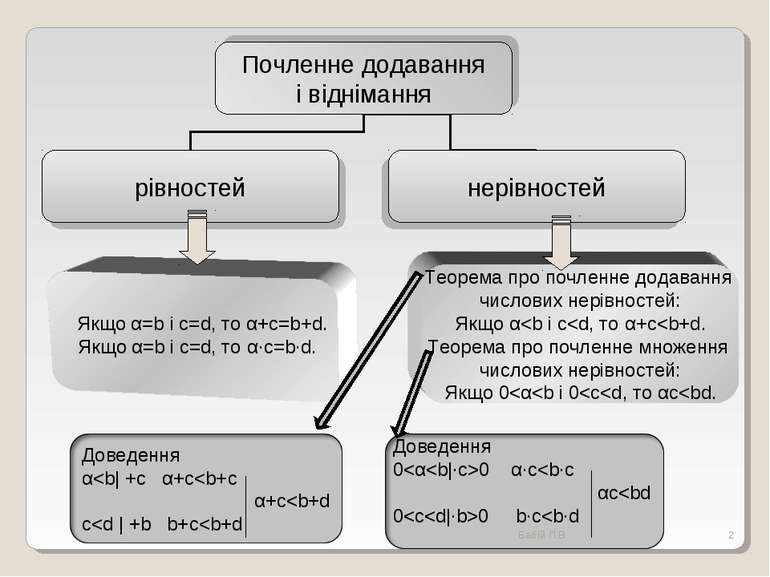
Тема: Почленне додавання і множення нерівностей. Мета: сформувати в учнів уявлення про почленне додавання та множення нерівностей; розглянути теореми про почленне додавання і почленне множення числових нерівностей та наслідків з них. * Бабій Л.В. Бабій Л.В.

Теорема про почленне додавання числових нерівностей: Якщо α

Сформулюй теорему словесно Якщо почленно додавати правильні нерівності однакового знака, залишивши їх спільний знак, то дістанемо правильну числову нерівність. Якщо почленно помножити правильні нерівності однакового знака, в кожній частині яких – додатні числа, залишивши їх спільний знак,то дістанемо правильну нерівність. * Бабій Л.В. Бабій Л.В.

Наслідок Якщо 0

Додайте почленно нерівності: 1) 5

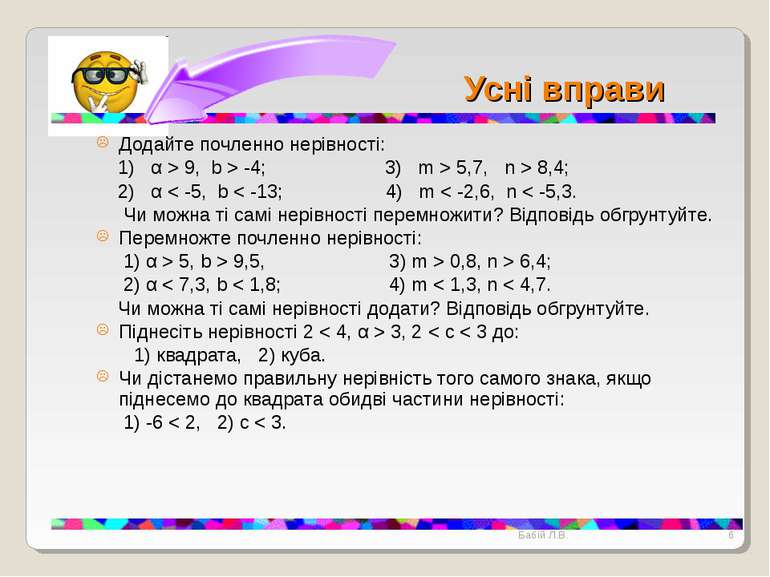
Усні вправи Додайте почленно нерівності: 1) α > 9, b > -4; 3) m > 5,7, n > 8,4; 2) α < -5, b < -13; 4) m < -2,6, n < -5,3. Чи можна ті самі нерівності перемножити? Відповідь обгрунтуйте. Перемножте почленно нерівності: 1) α > 5, b > 9,5, 3) m > 0,8, n > 6,4; 2) α < 7,3, b < 1,8; 4) m < 1,3, n < 4,7. Чи можна ті самі нерівності додати? Відповідь обгрунтуйте. Піднесіть нерівності 2 < 4, α > 3, 2 < c < 3 до: 1) квадрата, 2) куба. Чи дістанемо правильну нерівність того самого знака, якщо піднесемо до квадрата обидві частини нерівності: 1) -6 < 2, 2) c < 3. * Бабій Л.В. Бабій Л.В.

Вчимося доводити нерівності Щоб довести нерівність А ≤ В, тобто довести, що вона є правильною при заданих умовах, треба: скласти різницю лівої та правої частин нерівності; перетворити складену різницю так, щоб можна було визначити її знак; зробити висновок. Приклад. Довести нерівність α(α – 4) < (α – 2)2. Доведення. Розглянемо різницю α(α – 4) - (α – 2)2 = α2-4α - α2 + 4α – 4 = -4 < 0. Отже, α(α – 4) < (α – 2)2 при будь якому α. * Бабій Л.В. Бабій Л.В.