Презентація на тему:
Дослідження зв’язку між коренями і коефіцієнтами квадратного рівняння

Дослідження зв’язку між коренями і коефіцієнтами квадратного рівняння Таценко А.Г., вчитель математики ЗОШ № 19 м. Черкаси

Квадратні рівняння Квадратним рівнянням називається рівняння виду ax2+bx+c=0, де a, b, с R (a 0). Числа a, b, с називають коефіцієнтами квадратного рівняння: a - перший коефіцієнт, b - другий коефіцієнт, с - вільний член.

Зведене рівняння Якщо в рівнянні виду: ax2+bx+c=0, где a, b, с R а = 1, то квадратне рівняння виду x2+px+q=0 називається зведеним.

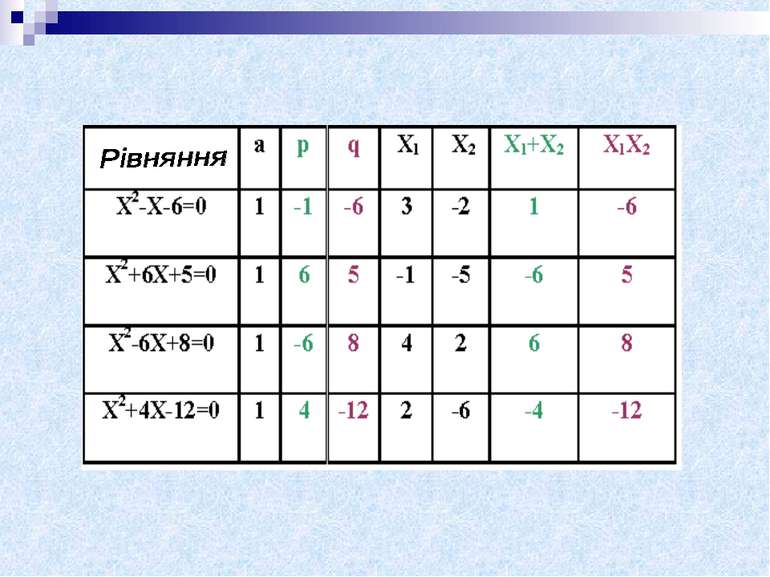
Твердження №1: Нехай х1 і х2 – корені рівняння х2+ pх + q =0. Тоді числа х1, х2 , p, q зв’язані рівностями: х1 + х2= -p, х1х2=q Твердження № 2: Нехай числа х1, х2, p,q зв’язані рівностями х1 + х2 = -p, х1х2=q. Тоді х1 і х2 – корені рівняння х2+ pх + q=0

Теорема Вієта: Числа х1 і х2 є коренями зведеного квадратного рівняння х2 +pх+q=0, тоді і тільки тоді, коли х1 +х2 = -p, х1х2 = q. Наслідок: х2 + pх + q=(х-х1)(х-х2).

Застосування теореми Вієта Теорема Вієта чудова тим, що, не знаючи коренів квадратного тричлена, ми легко можемо обчислити їх суму і добуток, тобто найпростіші симетричні вирази x1 + x2 і x1 x2.

Знаходження коренів Так, ще не знаючи, як знайти корені рівняння: x2 + 2x – 8 = 0, ми можемо вказати, що їх сума повинна бути рівною – 2, а добуток повинен дорівнювати – 8.

Франсуа Вієт Франсуа Вієт народився в 1540 році в Франції. Батько Вієта був прокурором. Син обрав професію батька і став юристом, закінчив університет в Пуату. В 1563 году він залишає юриспруденцію та стає вчителем у знатній родині. Саме викладання викликало у молодого юриста до математики. Вієт переїзджає в Париж, де легше взнати про досягнення відомих математиків Європи. З 1571 року Вієт займає важливі державні пости, але в 1584 році його звільнили та вислали з міста. Тепер він мав можливість серйозно займатися математикою. В 1591 году він видає трактат «Введенння в аналітичне мистецтво», де показав, що, оперуючи з символами, можно отримати результат, який можна застосовувати до будь-яких відповідних величин. Відома теорема була опублікована в цьому ж році. Гучну славу отримав при Генріхе lll під час Франко-Іспанської війни. На протязі двох тижнів, просидів за работою дні та ночі, він найшов ключ до іспанського шифру.

Ситуації, в яких можна використовувати теорему Вієта. 1. Перевірка правильності знайдених коренів. 2. Визначення знаків коренів квадратного рівняння. 3. Усне знаходження цілих коренів зведеного квадратного рівняння. 4. Скласти квадратне рівняння з заданими коренями. 5. Розкласти квадратний тричлен на множники.

Розв’яжіть наступні завдання: 1. Чи є числа 15 і 7 є коренями рівняння х2 - 22х + 105 = 0? 2. Визначте знаки коренів рівняння х2 + 5х – 36 = 0. 3. Знайти усно корені рівняння х2 - 9х + 20 = 0. 3. Скласти квадратне рівняння, коренями якого є числа 1/3 и 0,3. 4. Розкласти квадратний тричлен на множники х2 + 2х - 48.

Узагальнена теорема Вієта: Числа х1 і х2 є коренями квадратного рівняння ах2 + bх + с = 0, тоді і тільки тоді, коли х1 + х2 = -b/а, х1 х2 = с/а. Наслідок: ах2 + bх + c = а(х-х1)(х-х2).

Розв’язати наступні завдання: 1. У рівнянні х2 + pх – 32 = 0 один з коренів дорівнює 7. Знайдіть інший корінь і коефіцієнт p. 2. Один з коренів рівняння 10х2 - 33х + с = 0 дорівнює 5,3. Знайдіть інший корінь та коефіцієнт с. 3. Різниця коренів квадратного рівняння х2 - 12х + q = 0 дорівнює 2. Знайдіть q. 4. Визначте знаки коренів квадратного рівняння ( якщо вони існують), не розв’язуючи рівняння: 5х2 – х – 108 = 0. 5. Знайдіть b та розв’яжіть рівняння (b-1) х2 - (b+1)х = 72, якщо х1 = 3.

По праву гідно у віршах розкрита властивість коренів теореми Вієта. Що краще, скажи, сталості такої: – Помножиш корені і дріб уже готовий ? У чисельнику «с», у знаменнику «а»- Сума коренів теж буде дробу рівна; Хоч і з мінусом цей дріб , то не біда: У чисельнику «в», у знаменнику «а».